1. Reviewing the Proposed String Realization of Weyl Geometry
Previous papers have reviewed the Weyl geometry in which the parallel displacement of a vector around a closed curve admits an increment of vector magnitude. It was observed that the Weyl model associated increments of vector magnitude l with curvature states
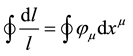 (1)
(1)
[1] . Adopting a proposal by F. London [2] , such states are admissible as physical states if and only if they satisfy a principle of gauge invariance
 (2)
(2)
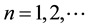 ; i.e. if and only if they preserve vector magnitude. In recent discussions, a string analogue of the Weyl model replaced the parallel displacements of vectors around closed curves with displacements of closed, spin-2 strings that swept out closed world tubes:
; i.e. if and only if they preserve vector magnitude. In recent discussions, a string analogue of the Weyl model replaced the parallel displacements of vectors around closed curves with displacements of closed, spin-2 strings that swept out closed world tubes:
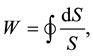 (3)
(3)
where S represented the length of the circulating string. This analogue of Weyl curvature was called W-curva- ture and was designated “W.” By hypothesis the W-curvature state (3) was regarded as an admissible physical state if and only if it satisfied a principle of gauge invariance
 (4)
(4)
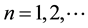 ; i.e. if and only if it preserved string length. The value n = 1 was regarded as corresponding to the closed nature of the world tube that was swept out by the postulated, closed, spin-2h string. The residue
; i.e. if and only if it preserved string length. The value n = 1 was regarded as corresponding to the closed nature of the world tube that was swept out by the postulated, closed, spin-2h string. The residue 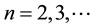 was associated with the periodic circulation of the closed string. Secondly the proposed model considered the compounded world tube that was generated when the outer circumference of a closed world tube (4) swept out a closed tube:
was associated with the periodic circulation of the closed string. Secondly the proposed model considered the compounded world tube that was generated when the outer circumference of a closed world tube (4) swept out a closed tube:
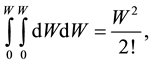 (5)
(5)
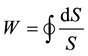 . The composite (5) was regarded as a physical state if and only if each of the two closed tubes satisfied a principle of gauge invariance
. The composite (5) was regarded as a physical state if and only if each of the two closed tubes satisfied a principle of gauge invariance
 . (6)
. (6)
The value n = 1 was regarded as describing the closed nature of the first world tube and n = 2 was regarded as enforcing the closed nature of the postulated “second order” closed tube that was swept out by the circulation of the first order tube (that corresponding to n = 1). Additional oscillations of the closed string and closed world tube were not described.
Finally a generalization
![]() (7)
(7)
of (5) resulted in a world tube of nth order. The compounded world tube (7) was regarded as having been established by the circulation of an (n-1)th order tube as this tube swept out a closed tube. Again the curvature states (7) were regarded as physical states if and only if they satisfied a principle of gauge invariance
![]() (8)
(8)
The value n = 1 enforced the closed nature of the first order world tube, n = 2 enforced the closed nature of the postulated “second order” closed tube which was swept out by the circulation of the first order tube, etc. The value n = 6 enforced the closed nature of the nth order world tube. Again, additional oscillations of the closed string, of the closed world tube etc. were not described.
Each of the W-curvature states (7) that was established by a principle of gauge invariance (8) was associated, by hypothesis, with a stable or stationary, spin-2h state
![]() (9)
(9)
where ![]() was a generic left-handed quark, where
was a generic left-handed quark, where ![]() represented a mass-less, left-handed spin-2h field and where
represented a mass-less, left-handed spin-2h field and where ![]() was a generic, right-handed anti-lepton which was of the same generation as
was a generic, right-handed anti-lepton which was of the same generation as ![]() and was characterized by an I3 value that was opposite that of
and was characterized by an I3 value that was opposite that of ![]() [3] . The composites
[3] . The composites ![]() were regarded as realizations of the “super-unified field” that was proposed earlier by this author (a field of spin-2h, which carries color, was of electrical charge 2/3 and was (I3)-neutral) [4] .
were regarded as realizations of the “super-unified field” that was proposed earlier by this author (a field of spin-2h, which carries color, was of electrical charge 2/3 and was (I3)-neutral) [4] .
2. A Review of Theoretical Fermions
The proposed model was calibrated by associating the gauge invariant W-curvature state ![]() of order n = 6 with the mass of the top quark:
of order n = 6 with the mass of the top quark:
![]() (10)
(10)
[5] . By hypothesis, proposed stationary curvature states![]() : n = 1, 2, 3, 4, 5 modeled the additional lepto-quark classes
: n = 1, 2, 3, 4, 5 modeled the additional lepto-quark classes![]() .
.
Specifically, an expression that is algebraically equivalent to expression (10) was obtained by dividing both sides of (10) by “6.” The result was
![]() (11)
(11)
Interpretation of this unfamiliar mass was deferred until after the massive states described by expressions (12), (13), (14) and (15) had been interpreted. Continuing, both sides of (11) were divided by “5” to produce
![]() . (12)
. (12)
The theoretical mass represented by expression (12) motivated the association of (12) with the I3 values and generation that correspond to ![]() and
and![]() , where
, where ![]() is the left-handed bottom quark and where
is the left-handed bottom quark and where ![]() re- presents the right-handed anti-tauon. Thus the mass that by hypothesis corresponds to m4 is that associated with the spin-2h composite
re- presents the right-handed anti-tauon. Thus the mass that by hypothesis corresponds to m4 is that associated with the spin-2h composite![]() , where
, where ![]() is a mass-less, left-handed, spin-2h field. The observed mass of the bottom quark
is a mass-less, left-handed, spin-2h field. The observed mass of the bottom quark ![]() is about 4.3 GeV/c2 and the observed mass of the anti-tauon
is about 4.3 GeV/c2 and the observed mass of the anti-tauon ![]() is about 1.7 GeV/c2 [5] . Thus the theoretically established mass of the postulated composite (12) closely parallels the mass that is observationally established. The bottom quark and the tauon were regarded as constituting I3 = −1/2 partners in a heavy fermion generation.
is about 1.7 GeV/c2 [5] . Thus the theoretically established mass of the postulated composite (12) closely parallels the mass that is observationally established. The bottom quark and the tauon were regarded as constituting I3 = −1/2 partners in a heavy fermion generation.
To observe a fourth state both sides of (12) were divided by “4” to produce
![]() (13)
(13)
The theoretical mass of expression (13) motivated the association of (13) with the I3 values and generation that correspond to ![]() and
and ![]() where
where ![]() represents the left-handed charmed quark and where
represents the left-handed charmed quark and where ![]() re- presents the right-handed anti-muon’s neutrino. Thus the mass
re- presents the right-handed anti-muon’s neutrino. Thus the mass ![]() was associated with the observed mass of the spin-2h composite
was associated with the observed mass of the spin-2h composite![]() . It was observed that the observationally determined mass of the spin-2h state
. It was observed that the observationally determined mass of the spin-2h state ![]() is about 1.5 GeV/c2 [5] , which is approximately equal to the mass that is theoretically established by expression (13). The mass of
is about 1.5 GeV/c2 [5] , which is approximately equal to the mass that is theoretically established by expression (13). The mass of ![]() is negligible in the context under consideration, so that the mass of the spin-2h state
is negligible in the context under consideration, so that the mass of the spin-2h state ![]() was associated with that of the charmed quark (1.5 GeV/c2). The charmed quark and the muon’s neutrino were regarded as I3 = +1/2 partners in a moderately heavy generation.
was associated with that of the charmed quark (1.5 GeV/c2). The charmed quark and the muon’s neutrino were regarded as I3 = +1/2 partners in a moderately heavy generation.
To introduce a fifth state, both sides of (13) were divided by “3” to produce
![]() (14)
(14)
The mass of expression (14) motivated the association of (14) with the I3 values and generation that correspond to the pair consisting of ![]() and
and![]() , where
, where ![]() represents the right-handed strangequark and
represents the right-handed strangequark and ![]() represents the left-handed anti-electron. Thus the mass
represents the left-handed anti-electron. Thus the mass ![]() was associated with the spin 2h composite
was associated with the spin 2h composite![]() . The observationally determined mass of
. The observationally determined mass of ![]() is about 0.5 GeV/c2 [5] , which is approximately equal to the theoretically determined value (14). Since the mass of
is about 0.5 GeV/c2 [5] , which is approximately equal to the theoretically determined value (14). Since the mass of ![]() is relatively negligible, the mass of the spin-2h state
is relatively negligible, the mass of the spin-2h state ![]() was associated with that of the strange quark. The right-handed strange quark and the right-handed electron were regarded as I3 = 0 partners in (what is in the proposed model regarded as) a light generation.
was associated with that of the strange quark. The right-handed strange quark and the right-handed electron were regarded as I3 = 0 partners in (what is in the proposed model regarded as) a light generation.
Finally, to observe a sixth state, both sides of (14) were divided by “2” to produce
![]() (15)
(15)
The mass of expression (15) motivated the association of (15) with the I3 values and generation that correspond to that of the spin-2h state![]() , where the mass of
, where the mass of ![]() is the mass that is obtained when the mass of the up quark and that of the down quark are averaged; and the mass of
is the mass that is obtained when the mass of the up quark and that of the down quark are averaged; and the mass of ![]() is the mass obtained when the mass of the anti-electron and that of the anti-electron’s neutrino are averaged. Similarly the I3 value of
is the mass obtained when the mass of the anti-electron and that of the anti-electron’s neutrino are averaged. Similarly the I3 value of ![]() is the I3 value that is obtained when the I3 value of the up quark and that of the down quark are averaged; and the I3 value of
is the I3 value that is obtained when the I3 value of the up quark and that of the down quark are averaged; and the I3 value of ![]() is the I3 value that is obtained when the I3 value of the anti-electron and that of the anti-electron’s neutrino are averaged. Thus the spin-2h state
is the I3 value that is obtained when the I3 value of the anti-electron and that of the anti-electron’s neutrino are averaged. Thus the spin-2h state ![]() was associated with an I3 value of zero and with the light generation. The observed mass of
was associated with an I3 value of zero and with the light generation. The observed mass of ![]() (the average of the mass of the up quark and that of the down quark) is about 0.25 GeV/c2 [5] , which closely approximates the theoretical mass described by (15). The mass of
(the average of the mass of the up quark and that of the down quark) is about 0.25 GeV/c2 [5] , which closely approximates the theoretical mass described by (15). The mass of ![]() is for our purposes negligible. Thus the observationally determined mass of the postulated state
is for our purposes negligible. Thus the observationally determined mass of the postulated state ![]() was associated with the average of the mass of the up quark plus that of the down quark.
was associated with the average of the mass of the up quark plus that of the down quark.
To interpret the mass of the composite that is described by expression (11), it was first observed that the left-handed muon ![]() is not included in the foregoing discussion. In this context the mass that is described by (11) was interpreted as that of the spin-2h composite
is not included in the foregoing discussion. In this context the mass that is described by (11) was interpreted as that of the spin-2h composite![]() . Accordingly the 7L was interpreted as an unobserved, left-handed quark that is characterized by I3 = −1/2 and 7L was regarded as a member of a moderately heavy generation. Finally, since the mass of
. Accordingly the 7L was interpreted as an unobserved, left-handed quark that is characterized by I3 = −1/2 and 7L was regarded as a member of a moderately heavy generation. Finally, since the mass of ![]() is negligible, the mass of the newly predicted quark that is associated with expression (11) was designated as approximately 30 GeV/c2.
is negligible, the mass of the newly predicted quark that is associated with expression (11) was designated as approximately 30 GeV/c2.
To further elaborate upon the relevant aspects of string theory, it is necessary to review the theory of super-gravitation.
3. A Review of SUGRA Interactions
To discuss super-gravitational interactions it is necessary to review the theory of pure super-gravity. Osp(1/4)- pure super-gravity on M4
L![]() (16)
(16)
is regarded as dual to the string background AdS7XS4 [6] . The Lagrangian density (16) is based upon the super-Poincare algebra
![]() , (17)
, (17)
where![]() . The
. The ![]() represent the translation group, the
represent the translation group, the ![]() constitute the adjoint representation of the Lorentz group and the
constitute the adjoint representation of the Lorentz group and the ![]() are components of the SUSY generator. The
are components of the SUSY generator. The ![]() describe all connection fields:
describe all connection fields:
![]() (18)
(18)
and transform under Osp(1/4) as
![]() . (19)
. (19)
The covariant derivative is
![]() (20)
(20)
and the curvature tensor is derived from![]() , where
, where
![]() (21)
(21)
[7] .
4. The Large Scale
String theory as proposed in Section 1 produces the six spin-2h curvature states ![]() which are described by expression (9) and which, by hypothesis, associate with the symmetry
which are described by expression (9) and which, by hypothesis, associate with the symmetry![]() , which is depicted by Figure 1. Depicted I3 values are those that characterize the left handed fermions in the states
, which is depicted by Figure 1. Depicted I3 values are those that characterize the left handed fermions in the states![]() , where SU(3) consists of the curvature classes
, where SU(3) consists of the curvature classes![]() ,
, ![]() and
and![]() , while
, while ![]() consists of the I3 conjugate classes
consists of the I3 conjugate classes![]() ,
, ![]() and
and![]() . By hypothesis the radii that separate the vertices of the Figure 1 configuration from the center of radial symmetry of that configuration are associated with the length of the string scale as postulated in Section 1. It can also be confirmed that every vertex of the Figure 1 symmetry is characterized by an electrical charge of 2/3. In this context one can introduce super-gravitational interactions that satisfy that Noether principle involving conservation of string scale and electrical charge and equivalent preservation of the Figure 1 symmetry. An example of this implicitly defined SUGRA interaction is as depicted in Figure 2. The Noether principle can also be stated in terms of conservation and preservation under gauge transformations.
. By hypothesis the radii that separate the vertices of the Figure 1 configuration from the center of radial symmetry of that configuration are associated with the length of the string scale as postulated in Section 1. It can also be confirmed that every vertex of the Figure 1 symmetry is characterized by an electrical charge of 2/3. In this context one can introduce super-gravitational interactions that satisfy that Noether principle involving conservation of string scale and electrical charge and equivalent preservation of the Figure 1 symmetry. An example of this implicitly defined SUGRA interaction is as depicted in Figure 2. The Noether principle can also be stated in terms of conservation and preservation under gauge transformations.
Since string theory as proposed in Section 1 has now incorporated position-independent SUGRA connections (e.g. the connections in the Figure 2 interaction), the curvature classes represented by expressions (7) and (9) are associated by hypothesis with the reduced version ![]() of the curvature tensor (21). In this context the curvature states that are described by expressions (7) and (9) are associated with
of the curvature tensor (21). In this context the curvature states that are described by expressions (7) and (9) are associated with
![]() (22)
(22)
where![]() : S is the length of the transported, closed string that is described in Section 1. The states (22)
: S is the length of the transported, closed string that is described in Section 1. The states (22)
are identified by hypothesis as admissible physical states if and only if they are established by gauge invariance:
![]() (23)
(23)
A large scale model is founded upon the postulated invariance of ![]() under (23) and the equivalent conservation by (23) of string scale and of the curvature
under (23) and the equivalent conservation by (23) of string scale and of the curvature ![]() from which the postulated model generates admissible increments of large scale expansion. In this context the relevant realization of the proposed symmetry consists of ever more massive states that cumulatively constitute a pre-galactic hierarchy. Each level of this hierarchy is associated with the introduction throughout the hierarchy of a new generation of fermions. Consequently, the radii that separate the vertices of Figure 3 from the center of radial symmetry of that configuration are associated by hypothesis with the string scale that was introduced in Section 1 and with the curvature
from which the postulated model generates admissible increments of large scale expansion. In this context the relevant realization of the proposed symmetry consists of ever more massive states that cumulatively constitute a pre-galactic hierarchy. Each level of this hierarchy is associated with the introduction throughout the hierarchy of a new generation of fermions. Consequently, the radii that separate the vertices of Figure 3 from the center of radial symmetry of that configuration are associated by hypothesis with the string scale that was introduced in Section 1 and with the curvature![]() .The three figures to which the proposed model refers are depicted below.
.The three figures to which the proposed model refers are depicted below.
![]()
Figure 1. Symmetry of fermion mass classes.
![]()
Figure 2. An admissible SUGRA interaction.
![]()
Figure 3. Symmetry of levels constituting the postulated galactic hierarchy.
If established boundary conditions are adopted, the geometry of the proposed model motivates a theoretical approximation of the total number of galaxies. Let us now consider this model.
The proposed model is calibrated in terms of a large-scale boundary condition that is based upon observation. Specifically if a constant of proportionality ![]() is defined by
is defined by
![]() , (24)
, (24)
then the phase transitions that are described by the expression (23) become
![]() (25)
(25)
The selection of base 10 is founded upon the observed boundary condition that galaxies are typically separated by a distance that is about ten times the diameter of the typical galaxy; that galactic clusters are typically separated by a distance that is about ten times the diameter of the typical galactic cluster etc.
The typical galactic cluster, which corresponds by hypothesis to n = 2, will be modeled in terms of local but globally typical boundary conditions. Observations of such conditions establish that the typical galaxy is about 105 light years (ly) in diameter, and that five galaxies populate the typical basic cluster. The local cluster is approximated as a volume that is enclosed by an abstract sphere and that is measured in terms of a number of galaxies; i.e. as a volume that is associated with the equation
![]() (26)
(26)
where R2 is the average radius of a typical local cluster in terms of a number of galaxies. Rounding to three digits, it is concluded that, typically,![]() . Utilizing the value R2 = 1.06, the Equation (26), and the boundary condition of homogeneity that is established by observation, and rounding to three digits, one determines the approximate radius R3, in terms of a number of galaxies, of a typical n = 3 state: R3 = (2(10)1.06 = 21.2). Utilizing R3 = 21.2 and rounding to three digits one determines the approximate value R4 in terms of a number of galaxies of a typical n = 4 state: R4 = (2(10)21.2 = 424). Utilizing the value R4 = 424 and rounding to three digits, one determines the radial value R5 of a typical n = 5 state: R5 = (2(10)424 = 8480). Finally, utilizing the value R5 = 8480, and rounding to three digits, one determines the value R6 of a typical n = 6 state: R6 = (2(10)8480 = 169,600); or (rounding to three digits) 170,000.
. Utilizing the value R2 = 1.06, the Equation (26), and the boundary condition of homogeneity that is established by observation, and rounding to three digits, one determines the approximate radius R3, in terms of a number of galaxies, of a typical n = 3 state: R3 = (2(10)1.06 = 21.2). Utilizing R3 = 21.2 and rounding to three digits one determines the approximate value R4 in terms of a number of galaxies of a typical n = 4 state: R4 = (2(10)21.2 = 424). Utilizing the value R4 = 424 and rounding to three digits, one determines the radial value R5 of a typical n = 5 state: R5 = (2(10)424 = 8480). Finally, utilizing the value R5 = 8480, and rounding to three digits, one determines the value R6 of a typical n = 6 state: R6 = (2(10)8480 = 169,600); or (rounding to three digits) 170,000.
It is assumed that each radius is established by a class of phase transitions which produces a space-like blister that is initially vacuous in its interior and is thinly bounded by a mass energy distribution. By hypothesis each blister is ultimately converted into a 3-dimensional distribution (as the spherical mass-energy distribution is inwardly dispersed). By hypothesis, each filled-in blister becomes an element of a larger spherical distribution (initially vacuous interior) that is generated by the next class of phase transitions. Near the event horizon spherical distributions of mass-energy are, by hypothesis, not yet inwardly dispersed. It is therefore assumed that the final radius that is calculated above is the radius of a spherical distribution that involves the entire galactic hierarchy. The area of this spherical distribution is now calculated in terms of a number of galaxies.
![]() (27)
(27)
[8] . The number of galaxies indicated by expression (27) closely parallels the approximation that is indicated by observation.
5. Conclusions
Previous discussions that attribute mass to a string analogue of Weyl curvature are reviewed and adopted as a foundation for proposed large scale considerations. A string analogue of Weyl curvature is again described as emerging when closed spin-2h strings sweep out closed world tubes. A second degree of freedom and corresponding class of world tubes are described as occurring when world tubes themselves sweep out closed tubes etc. The proposed hypothesis is described as paralleling Wheeler’s ideal, which attributes mass to space-time curvature [9] . The model that is reviewed correctly approximates the masses of observed quarks and of the tauon and predicts a new quark of (approximately) 30 GeV/c2.
Postulated curvature classes are associated, by hypothesis, with composite masses![]() , where
, where ![]() de-
de-
notes a mass-less spin-2h field and where ![]() and
and ![]() respectively denote an LH quark and an RH anti-lep-
respectively denote an LH quark and an RH anti-lep-
ton that are characterized by opposite I3 values and share a common generation. The composite masses ![]()
form a symmetry, the preservation of which is equivalent to the conservation of electrical charge and of string scale. SUGRA interactions that preserve the relevant symmetry can therefore be precisely defined. In this context, moreover, gauge transformations that establish the curvature classes associate, by hypothesis, with a second realization of the originally generated symmetry, the preservation of which, by hypothesis, is equivalent to the
conservation of string length and the conservation of the curvature ![]() from which the postulated
from which the postulated
model generates admissible increments of large scale expansion. The latter symmetry is associated by hypothesis with the large scale structure of the observable universe, thereby motivating a theoretical approximation of the total number of galaxies. This result parallels the approximation that is indicated by observation.
Acknowledgements
Figures are designed by R. James Towe.