Large Deformation Characterization of Porcine Thoracic Aortas: Inverse Modeling Fitting of Uniaxial and Biaxial Tests ()
1. Introduction
Due to the difficulty of testing soft tissues such as arteries in vivo, mechanical testing of arteries in vitro is often preferred. Uniaxial and biaxial testing has been used to characterize anisotropic materials such as arteries, although methodological aspects are still debated [1] - [3] . For instance, microsurgical or fishing hooks, crocodile grips, grip clamps and other kinds of fixtures have been employed to attach the sample to the actuators of the uniaxial or biaxial apparatus. According to the Saint-Venant principle, stress distribution in a body is uniform away from the points of application of the load. This implies that local stress concentration phenomena occur close to the point of application of the load (edges of the sample), depending on the way the load is applied. Therefore, strain is typically measured far from the edges of the sample. This approach has been demonstrated both on uniaxial [4] - [6] and biaxial experiments [7] - [15] . In biaxial mode, hooks or sutures are typically attached along the four borders of a square sample of arterial wall tissue [16] - [19] , so as to allow stretch of the borders along their length. However, local stress concentration can cause the sample to fail at the hook puncture site. Cruciform samples clamped with grips are often used for testing industrial materials when sample thickness distribution can be controlled [20] [21] . However, this type of sample geometry creates high stresses in the curved parts of the sample boundaries, as is demonstrated with computer simulations on various biaxial sample shapes and boundary conditions [22] .
Inverse modeling has been used to obtain material properties from experiments where an analytical solution is difficult to obtain [23] . Because inverse modeling can take into account the well-defined boundary conditions of biaxial cruciform samples, the main objective of this study is to evaluate the feasibility of inverse modeling for biaxial testing of cruciform samples over a wider range of strains than is possible with square samples. A secondary objective is to investigate whether data obtained from uniaxial tests performed in 2 orthogonal directions can accurately predict biaxial behavior, and vice versa.
2. Materials and Methods
2.1. Experimental Setup
Seven thoracic aortas were harvested within the day of death of pigs from a local slaughterhouse. Upon arrival, any visible connective tissue was dissected away from the external wall of the artery. Then the artery was cut open along its length, and cut out in rectangular, square and cruciform shapes (Figure 1). The rectangular samples were tested uniaxially while the square and cruciform samples were tested biaxially. A total of 16 samples were obtained from the 7 aortas: 4 cruciform samples from 2 aortas along with 8 rectangular and 4 square samples from 5 aortas. Thickness was measured with a vernier caliper. Samples were stored in saline solution at 4˚C for no longer than 4 days prior to testing.
The biaxial test bench (Bose Corporation, Minnetonka, MN), shown in Figure 2, includes four linear actuators capable of applying a peak force of 200 N and a maximum velocity of 3.2 m/s, over a displacement range of 24 mm (12 mm for each actuator). Samples can be mounted in horizontal configuration inside a saline bath heated at body temperature (37˚C). Grip clamps (for cruciform and rectangular samples) or fishing hooks (for square samples) can be used to attach the sample to arms extending from the actuators over the top of the bath. Displacement transducers are built in each of the four actuators. Two of the actuators (in x and y directions) are equipped with a 222 N (50 lbs) load cell. An optical strain extensometer includes a CCD camera located above the sample to record the sample deformation during the test, and a software capable of tracking the position of four ink dots on the sample and extracting online the strains in the two principal directions (ε11, ε22) and the shear strain (ε12).
Eight rectangular samples were tested uniaxially: four in the circumferential direction and four in the axial direction. Preliminary destructive tests revealed that failure rarely occurs below a nominal stretch ratio of 2.00.
![]()
Figure 1. Sample dimension in millimetres for (a) Uniaxial testing: rectangular sample clamped with grips; and ((b), (c)) biaxial testing: (b) Cruciform sample clamped with grips; (c) Square sample attached with hooks.
![]()
Figure 2. (a) Biaxial test bench; (b) Cruciform setup; (c) Square setup.
Therefore a 1.80 nominal stretch ratio was applied (8.00 mm displacement by each actuator). The forces were measured with one load cell. The original length of the sample was taken as the distance between the pair of grips (Figure 1(a)).
Four cruciform samples were tested biaxially. An equal displacement on each of the four grips was applied. The forces at the grips were measured with the two load cells. In cruciform samples, the maximum displacement allowed by each actuator (12 mm) was applied, creating a non uniform strain distribution in the sample. This corresponds to an average nominal stretch ratio of about 1.60, calculated using the distance between facing grips.
Four square samples were also tested biaxially. Threads were used to attach four fishing hooks to each side of the sample. The threads were connected to the arms of the actuators with a pulley system that allowed maintaining an equal tension in each thread. A specially designed jig was used to ensure that the hooks were always placed at the same position on the sample. The forces at the arms of the actuators were measured with the two load cells. Four dots, each one located 8.5 mm apart of the axis center, were printed in a square pattern on the center of the top surface of the sample using a water resistant oil-based quick drying ink. The deformation at the center of the sample was measured using the optical strain extensometer.
In preliminary tests, failure at the hook puncture hole due to the high stress concentration occurred between 18 and 22 mm displacement. Therefore, the displacement was limited to 16 mm, corresponding to an average nominal stretch ratio of 1.64, calculated from the distance between the hooks on the parallel edges of the sample.
For all tests, a triangular wave form displacement at a one Hertz frequency was applied for 10 pre-condition- ing cycles [24] and 10 steady-state cycles. The sampling rate of the force measurements was set so that forces were measured at the same stretch values in each cycle, therefore allowing the calculation of an average force- stretch curve over the last 10 cycles. For all the samples tested, the experimental data obtained (such as sample thickness and the material load force-stretch data), in uniaxial and biaxial testing, were statistically analyzed and are presented as the mean value ± one standard deviation.
2.2. Inverse Modeling
In order to adjust the parameters of this model, the inverse modeling technique was used. In this approach, finite element simulations of the experiment are performed by applying either displacement or force conditions, on a mesh of the same size and shape as the sample. In the present work, IMI’s large deformation finite element software was used, with a convergence criterion of 0.01 mm on nodal displacements, of 1% on nodal forces. This software has been validated for predicting molten polymer forming processes such as blow molding and thermoforming [25] [26] . Although the thoracic aorta has been shown to be anisotropic [27] [28] , for the purpose of demonstrating the inverse modeling approach the aorta behavior was modeled using an isotropic constitutive model, the Mooney-Rivlin [29] model (see Appendix for equation details), as did others [19] [30] - [35] .
A set of initial values for the material properties is input. The simulation predicts the reaction forces at the boundaries or the displacement of the nodes corresponding to the ink dots in the center of the sample. The material properties are then adjusted using an optimization technique until a set of force-displacement experimental data matches the values calculated by the model. In this work, the sequential quadratic programming (SQP), a second order optimization method of Design Optimization Tools (DOT) software [36] , was used.
For the case of biaxial cruciform extension (Figure 3), displacement boundary conditions were applied to the mesh and reaction forces in the circumferential (x) and axial (y) directions were simultaneously calculated by the finite element software. In the optimization loop, the material properties were iteratively adjusted until the following objective function was minimized:
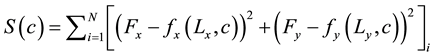(1)
where c is the vector of unknown material properties; Lx and Ly are the applied displacements; Fx and Fy are the experimentally measured reaction forces at the grips; and fx(Lx, c) and fy(Ly, c) are the reaction forces predicted by the finite element model. N is the total number of data points (L, F) gathered in the experiment. Mooney- Rivlin parameters (a10, a01, a11, a20, a30) are the components of vector c. In order to obtain fx(Lx, c) and fy(Ly, c), first, an initial guess of material parameters is made; second, the model predicts Total (T), Cauchy (σ), and second Piola-Kirchhoff (S) stresses by using the first and second invariants of the Green-Cauchy tensor defined for
![]()
Figure 3. Schematic representation of the inverse modeling technique used to obtain the material properties for the biaxial experiments with a cruciform sample.
Mooney-Rivlin Strain Energy Density Function (SEDF). Finally, the reaction forces are estimated using sample’s area.
Table 1 describes the applied boundary conditions and the predicted values used for each type of test. Similarly as in biaxial tests with cruciform samples, in uniaxial extension tests, displacement conditions were applied and reaction forces were predicted at the grips. However, two objective functions were defined, one for each direction:
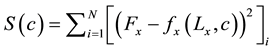(2)
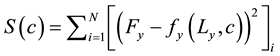(3)
Therefore, different material properties were obtained for the circumferential and for the axial directions, from the uniaxial extension experimental data.
In biaxial tests with square samples, forces were applied to each one of the nodes corresponding to the location of the hook sites, and strains were predicted at nodes corresponding to the location of the ink dots. Hence, the following objective function was minimized:
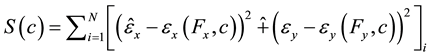(4)
where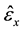
, 
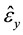are the measured strains at the ink dot locations, and
, 
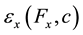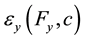are the predicted strains at the ink dot locations.
The finite element meshes used for simulation of uniaxial, biaxial cruciform and biaxial square tests are shown in Figure 4. Only the part of the sample free to deform between the pair of grip clamps was meshed for uniaxial (Figure 4(a)) and biaxial cruciform (Figure 4(b)) simulations. Because of symmetry, only one quarter of the cruciform sample area (Figure 4(b)) was simulated, which reduced computational time. In simulations of uniaxial extension tests and of biaxial tests with cruciform samples, the experimentally measured displacements were applied to the nodes located on the appropriate boundaries of the mesh. Predicted reaction forces distributed on the boundary nodes were summed for each tab of the sample and multiplied by 2 to account for symmetry, for comparison with experimental data. The use of reaction forces at the boundaries allows considering the deformation of the whole sample rather than a just sub-domain. The mesh used for the simulation of biaxial tests with a square sample is the square bounded by the perimeter traced by the hook puncture sites (Figure 4(c)). In simulations of the biaxial tests with square samples, experimentally measured forces divided by the number of hooks per sample edge (4) were applied to the nodes located at the hooks puncture sites. The ink dots at the center of the square samples define a subdomain, as described in Seshaiyer and Humphrey [23] , in which stresses and strains are considered uniformly distributed.
![]()
Figure 4. Undeformed meshes and boundary conditions for (a) Uniaxial extension tests; (b) Biaxial tests with cruciform samples; and (c) Biaxial tests with square samples.
![]()
Table 1. Shape, attachment method, applied conditions and predicted values for each type of experimental test performed.
3. Results
3.1. Experimental Results
The mean thickness of all tested specimens tested was 2.4 ± 0.4 mm. Figure 5 shows the experimental force data plotted against the “nominal” stretch ratio. For the square samples, the nominal stretch ratio was calculated using the ink dots. For the uniaxial rectangular and the biaxial cruciform samples, the nominal stretch ratio was calculated using the distance between the grips. In the rectangular samples, the stretch ratio is nearly uniformly distributed because the sample is 5 times longer than it is wide and therefore border effects can be neglected. However, in the cruciform samples the stretch ratio is also not uniformly distributed because of sample shape. This makes very difficult the comparison between experimental results from different tests.
Figure 5 shows the variability between samples as well as the anisotropic behavior of the arterial tissue. For all three types of tests, nonlinear behavior was observed, and differences between samples were small. In uniaxial extension tests (Figure 5(a)) and biaxial tests with square samples (Figure 5(c)), the samples were consistently stiffer in the circumferential direction than in the axial direction. Differences between samples and between directions were smallest in biaxial tests with cruciform samples (Figure 5(b)). Higher nominal stretch ratios were reached in the cruciform samples than in the square samples.
3.2. Inverse Modeling Results
Table 2 summarizes the adjusted Mooney-Rivlin parameters for each type of extensional test. For uniaxial tests, one set of parameters was obtained for each direction. For biaxial tests with cruciform and square samples, one set of parameters for both directions were obtained by simultaneously fitting circumferential and axial experimental data. Each parameter was limited to a −104 kPa to 104 kPa value range. Repeated optimization with different initial parameter values consistently converged towards the same solution. The computed circumferential and axial forces obtained using the Mooney-Rivlin fitted parameters from Table 2 in uniaxial, biaxial cruciform
![]()
Figure 5. Force-stretch ratio curves for (a) Uniaxial extension; (b) Biaxial testing with cruciform samples; and (c) Biaxial testing with square samples. Circumferential data are represented by dashed lines and hollow symbols. Axial data are represented by solid lines and solid symbols.
![]()
Table 2. Mooney-Rivlin fitted parameters.
and biaxial square are shown in Figure 6. For each type of test, a close fit was obtained between the model and the experimental data. In biaxial tests, the model was adjusted in between the circumferential and the axial data points. Figure 7(a) shows the value of the objective function plotted against the iteration number in the optimization loop, for three different initial guesses. The objective function was evaluated 50 times in iterations 0 (initial guess) to 6. Figure 7(b) illustrates optimization of one of the material parameter, a30, using three different initial guesses.
3.2.1. Uniaxial Fit
Figure 8 shows that the stress and stretch ratio distributions are non uniform close to the free edges of the sample. The local stretch ratio ranges from 1.70 to 1.82, for a nominal stretch ratio of 1.80. Mooney-Rivlin model parameters adjusted to the experimental uniaxial data were used to simulate the uniaxial and biaxial tests. The force-stretch curves for the experimental and simulated data are plotted in Figure 9. Although an excellent fit is observed between the uniaxial data and uniaxial simulation, the Mooney-Rivlin model adjusted to the uniaxial data does not predict well the biaxial behavior, especially in the nonlinear part of the curve at high stretch ratios.
![]()
Figure 6. Mooney-Rivlin experimental and computed reaction forces versus stretch ratios: (a) Circumferential and (b) Axial directions for uniaxial tests; (c) Biaxial tests with cruciform samples and (d) Biaxial tests with square samples.
![]()
(a) (b)
Figure 7. Optimization of the Mooney-Rivlin parameters for a biaxial test with a cruciform sample. (a) Objective function, and (b) Parameter a30 values as a function of iteration number, for three different initial guesses for material parameters: Case_A (all parameters = 0.1 MPa), Case_B (all parameters = 1.0 MPa), and Case_C (all parameters = 0.0001 MPa).
3.2.2. Biaxial Cruciform Fit
Figure 10 shows that the stress distribution is non-uniform in the cruciform sample, highest stresses being located at the curved boundaries, and lowest stresses close to the center of the full sample (upper left corner of the quarter-sample). Stretch ratios range from 1.24 to 1.65 for a nominal stretch ratio of 1.60.
In Figure 11, the parameters adjusted to the cruciform biaxial tests were used to simulate all types of tests. Since Mooney-Rivlin model is isotropic and a biaxial test was used, the parameters were adjusted simultaneously to the axial and circumferential experimental data points, contrarily to Figure 9 where different parameters were obtained for both directions. In this case, the agreement between cruciform experimental and simulated data is good, with the best predictions under 1.5 stretch ratios. The modeled curve fitted slightly better axial rather than circumferential forces below 1.4 stretch ratios. The Mooney-Rivlin model adjusted to the cruciform biaxial data was able to fit the uniaxial data up to stretch ratios of 1.5, but underestimated the biaxial behaviour of the square samples.
![]()
Figure 8. Deformed configurations at 1.80 nominal stretch ratio for rectangular mesh in uniaxial tension: distributions of (a) Stress and (b) Stretch ratio in the principal direction.
![]()
Figure 9. Simulated uniaxial and biaxial tests using Mooney-Rivlin parameters fitted to uniaxial experimental data: (a) Circumferential and (b) Axial force-stretch curves.
![]()
Figure 10. Deformed configurations at 1.60 nominal stretch ratio for cruciform mesh in biaxial stretching: distribution of (a) Stress and (b) Stretch ratio in the principal direction.
![]()
Figure 11. Simulated uniaxial and biaxial tests using Mooney-Rivlin parameters fitted to biaxial experimental data with cruciform samples: (a) Circumferential and (b) Axial force-stretch curves.
3.2.3. Biaxial Square Fit
In Figure 12, the stress and stretch ratio distributions are presented for the square sample under biaxial stretching. The stress distribution in biaxial extension is non-uniform and maximal close to the hook punctures sites, and mostly uniform near the center of the sample. The maximum stresses in this simulation are almost three times the values of the maximum stresses for the simulated rectangular and cruciform geometries (square: 1.90 MPa; cruciform: 0.43 MPa; rectangular: 0.65 MPa). Stretch ratios span from 1.18 to 1.95 for a nominal stretch ratio of 1.45 calculated from the ink dots.
Figure 13 shows the simulation results for all types of tests, using the Mooney-Rivlin parameters fitted to the square biaxial test results. The predictions of cruciform biaxial behavior and uniaxial behavior were largely overestimated compared to experimental results.
4. Discussion
Small sample variability between the axial force-stretch curves of the samples tested uniaxially and biaxially was found in this work. Circumferential data had a slightly higher variability, particularly in the biaxial square data. Prendergast et al. [19] found higher variability between square samples tested biaxially than was observed in this study, although the location of the samples along the aorta was not specified in their study. In the present study, higher forces were consistently observed in the circumferential direction in all 16 thoracic aorta samples tested, regardless of the test method (uniaxial, biaxial cruciform, biaxial square). This would justify further investigation of the inverse modeling technique with anisotropic constitutive models.
The inverse modeling technique was demonstrated to be a useful tool to tune constitutive models to experimental data. However, Mooney-Rivlin parameters obtained from each type of test vary greatly in this study. They are also very different from those reported by Prendergast et al. [19] . This might be due to the high number of parameters in the Mooney-Rivlin model and the fact that multiple combinations of widely different parameter values can produce similar stress-strain curves for a single deformation mode. Also, the Mooney-Rivlin
![]()
Figure 12. Deformed configurations at 1.64 nominal stretch ratio (at the puncture sites) for square mesh in biaxial stretching: distribution of (a) Stress and (b) Stretch ratio in the principal direction.
![]()
Figure 13. Simulated uniaxial and biaxial tests using Mooney-Rivlin parameters fitted to biaxial experimental data with square samples: (a) Circumferential and (b) Axial force-stretch curves.
model fitted to the cruciform biaxial data predicted well the uniaxial behavior up to stretch ratios of 1.5. This suggests that additional information on the material behaviour at higher stretch ratios than can be reached in biaxial tests might be obtained from uniaxial tests. Therefore, the inverse modeling method could be further improved by simultaneously fitting the results of complementary uniaxial and biaxial tests.
The agreement between biaxial and uniaxial simulations using the same material parameters was better when the parameters were obtained from the biaxial experiments with cruciform samples, than from the biaxial experiments with square samples. This might be due to the fact that the biaxial tests with the square samples do not take into account the high stretch ratios outside of the square area defined by the four ink dots. Because of stress concentration, failure occurred at the hook puncture sites before a stretch ratio of 1.5 could be reached at the center of the specimen. In contrast, the inverse modeling technique used with cruciform biaxial tests allows taking into account the whole behavior of the sample, including high stresses on curved borders, therefore allowing to reach maximum stretch ratios up to 1.64 in the sample.
Waldman and Lee [37] have observed a higher apparent stiffness when testing square samples of soft tissue with grip clamps than with sutures. In both types of tests, the stretch ratios were measured by tracking the position of points near the center of the specimen. They concluded that existing biaxial tests cannot reflect the properties of tissues in vivo and that more work needs to be done to standardize the boundary conditions in order to produce a uniform stress distribution in the center of the sample, where the deformations are measured. Our study shows that the inverse modeling technique allows taking into account the boundary conditions of the test and the sample geometry, circumventing the need to make measurements of stretch ratio away from the boundaries of the sample where the stress distribution is assumed to be uniform.
Advantages of cruciform samples over square samples include: 1) characterization over a higher deformation range, hence better prediction of behavior at large deformations; 2) simpler data acquisition through the use of actuator displacement rather than extensovideometry; 3) easier attachment of sample with grip clamps rather than sutures. However, the nonuniform stress distribution in cruciform samples requires the use of inverse modeling adjustment of constitutive model parameters.
5. Conclusion
We have reported uniaxial and biaxial experimental data of porcine aortas in vitro. We found that the highly nonlinear behavior of the arterial wall under large deformation was more easily and precisely measured biaxially using cruciform samples with grip clamps, than using square samples with hooks and sutures. Inverse modeling can be used to fit the material parameters of constitutive models, such as Mooney-Rivlin, to biaxial data measured on cruciform samples. More work is required in order to define the optimal set of experiments, and thus, to use the inverse modeling method to fit anisotropic, viscoelastic or active (muscle tone) models of soft tissues.
Acknowledgements
This research was possible thanks to the PhD scholarship given by the Mexican Council of Science and Technology (Consejo Nacional de Ciencia y Tecnología), CONACYT; and the support of the Industrial Materials Institute (IMI), CNRC-NRC and the Department of Biological & Chemical Engineering of the University of British Columbia. The authors would also like to thank Marc-Andre Rainville for his guidance and assistance in sample preparation and mechanical testing.
Appendix
Constitutive Equation
In the last years, several SEDF (Strain Energy Density Function), which are a measure of the energy stored in the material as a result of deformation, were developed and used to predict the mechanical properties of soft tissues. Most of these models make the assumption that the material is isotropic, instead of considering the anisotropy (due to the organized arrangement of the collagen components) of the arterial wall. Nevertheless, they can be used to simulate the deformation of the arterial wall in special cases, such as that corresponding to axial extension of arterial samples. SEDF selected is used to estimate Second Piola-Kirchhoff stress tensor (S) as follows:
![]()
(A.1)
![]()
(A.2)
where W is the Strain Energy Density Function; ![]()
are components of the second Piola-Kirchhoff stress tensor, the Green-Lagrange strain tensor (E), the finite strain deformation tensor (F), and the identity unit tensor (δ), respectively.
In finite deformations the second Piola-Kirchhoff stress tensor is used to relate forces in the reference configuration to areas in the same reference configuration. In contrast, the Cauchy stress tensor (σ) is used to express the stress relative to the current configuration. Under infinitesimal deformations both stresses are identical. Second Piola-Kirchhoff stress tensor is related to Cauchy and total stress tensors as follows:
![]()
(A.3)
![]()
(A.4)
where σij are the components of the Cauchy stress tensor (σ); Tij are the components of the total stress (T); the Jacobian (J) is defined as the determinant of the finite strain deformation tensor; and p is the hydrostatic pressure. In incompressible materials the Jacobian is equal to one (J = detF = 1).
Subject to the regularity assumption that W is continuously differentiable infinitely many times with respect to the 1st (I1), 2nd (I2), and 3rd (I3) invariants of the Green-Cauchy tensor (right), we may write W as an infinite series in powers of![]()
, ![]()
, ![]()
, where ![]()
are material parameters (constants):
![]()
(A.5)
The Mooney-Rivlin model selected in this investigation is a function of the 1st (I1) and 2nd (I2) invariants of the Green-Cauchy tensor (right). Its strain energy function is written as:
![]()
(A.6)
Moreover, I1 and I2 can be written as a function of the principal stretch ratios:
![]()
(A.7)
![]()
(A.8)
The Mooney-Rivlin model selected has five parameters (a10, a01, a11, a20, a30), all of them in MPa. The corresponding stress component of the stress tensor can be obtained when the strain density function is differentiated with respect to the corresponding strain component. This procedure is done by the finite element method by solving the equations described above.