On Elliptic Problem with Singular Cylindrical Potential, a Concave Term, and Critical Caffarelli-Kohn-Nirenberg Exponent ()
1. Introduction
In this paper, we consider the multiplicity results of nontrivial nonnegative solutions of the following problem 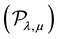
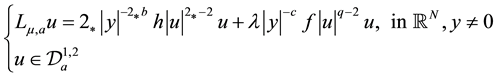
where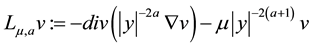 , where each point x in
, where each point x in  is written as a pair
is written as a pair  where k and N are integers such that
where k and N are integers such that 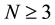 and k belongs to
and k belongs to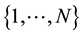 ,
, 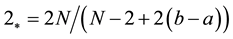
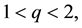
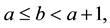
 is the critical Caffarelli-Kohn-Nirenberg exponent,
is the critical Caffarelli-Kohn-Nirenberg exponent,  ,
, 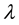
 is a real parameter,
is a real parameter,  , h is a bounded positive function on
, h is a bounded positive function on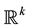 .
. ![]() is the dual of
is the dual of![]() , where
, where ![]() and
and ![]() will be defined later.
will be defined later.
Some results are already available for ![]() in the case
in the case![]() , see for example [1] [2] and the references
, see for example [1] [2] and the references
therein. Wang and Zhou [1] proved that there exist at least two solutions for ![]() with
with![]() ,
,
![]() and
and![]() , under certain conditions on f. Bouchekif and Matallah [3] showed the
, under certain conditions on f. Bouchekif and Matallah [3] showed the
existence of two solutions of ![]() under certain conditions on functions f and h, when
under certain conditions on functions f and h, when![]() ,
, ![]() ,
, ![]() and
and![]() , with
, with ![]() a positive constant.
a positive constant.
Concerning existence results in the case![]() , we cite [4] [5] and the references therein. Musina [5] con- sidered
, we cite [4] [5] and the references therein. Musina [5] con- sidered ![]() with
with ![]() instead of a and
instead of a and![]() , also
, also ![]() with
with![]() ,
, ![]() ,
, ![]() , with
, with ![]() and
and![]() . She established the existence of a ground state solution when
. She established the existence of a ground state solution when ![]() and
and
![]() for
for ![]() with
with ![]() instead of a and
instead of a and![]() . She also showed that
. She also showed that ![]() with
with![]() ,
, ![]() ,
, ![]() does not admit ground state solutions. Badiale et al. [6] studied
does not admit ground state solutions. Badiale et al. [6] studied ![]() with
with![]() ,
, ![]() ,
, ![]() and
and![]() . They proved the existence of at least a nonzero nonnegative weak solution u, satis- fying
. They proved the existence of at least a nonzero nonnegative weak solution u, satis- fying ![]() when
when ![]() and
and![]() . Bouchekif and El Mokhtar [7] proved that
. Bouchekif and El Mokhtar [7] proved that ![]() ad- mits two distinct solutions when
ad- mits two distinct solutions when![]() ,
, ![]() with
with![]() ,
, ![]() , and
, and ![]()
where ![]() is a positive constant. Terracini [8] proved that there is no positive solutions of
is a positive constant. Terracini [8] proved that there is no positive solutions of ![]() with
with![]() ,
, ![]() when
when![]() ,
, ![]() and
and![]() . The regular problem corresponding to
. The regular problem corresponding to ![]() and
and ![]() has been considered on a regular bounded domain
has been considered on a regular bounded domain ![]() by Tarantello [9] . She proved that, for
by Tarantello [9] . She proved that, for![]() , the dual of
, the dual of![]() , not identically zero and satisfying a suitable condition, the problem considered admits two distinct solutions.
, not identically zero and satisfying a suitable condition, the problem considered admits two distinct solutions.
Before formulating our results, we give some definitions and notation.
We denote by ![]() and
and![]() , the closure of
, the closure of ![]() with respect to the norms
with respect to the norms
![]()
and
![]()
respectively, with ![]() for
for![]() .
.
From the Hardy-Sobolev-Maz’ya inequality, it is easy to see that the norm ![]() is equivalent to
is equivalent to![]() . More explicitly, we have
. More explicitly, we have
![]()
for all![]() .
.
We list here a few integral inequalities.
The starting point for studying![]() , is the Hardy-Sobolev-Maz’ya inequality that is particular to the cylindrical case
, is the Hardy-Sobolev-Maz’ya inequality that is particular to the cylindrical case ![]() and that was proved by Maz’ya in [4] . It states that there exists positive constant
and that was proved by Maz’ya in [4] . It states that there exists positive constant ![]() such that
such that
![]() (1.1)
(1.1)
for any![]() .
.
The second one that we need is the Hardy inequality with cylindrical weights [5] . It states that
![]() (1.2)
(1.2)
It is easy to see that (1.1) hold for any ![]() in the sense
in the sense
![]() (1.3)
(1.3)
where ![]() positive constant,
positive constant, ![]() ,
, ![]() , and in [10] , if
, and in [10] , if ![]() the embedding
the embedding ![]() is compact, where
is compact, where ![]() is the weighted
is the weighted ![]() space with norm
space with norm
![]()
Since our approach is variational, we define the functional J on ![]() by
by
![]()
with
![]()
A point ![]() is a weak solution of the equation
is a weak solution of the equation ![]() if it satisfies
if it satisfies
![]()
with
![]()
![]()
![]()
Here ![]() denotes the product in the duality
denotes the product in the duality![]() ,
,![]() .
.
Let
![]()
From [11] , ![]() is achieved.
is achieved.
Throughout this work, we consider the following assumptions:
(F) there exist ![]() and
and ![]() such that
such that![]() , for all x in
, for all x in![]() .
.
(H) ![]()
Here, ![]() denotes the ball centered at a with radius r.
denotes the ball centered at a with radius r.
In our work, we research the critical points as the minimizers of the energy functional associated to the problem ![]() on the constraint defined by the Nehari manifold, which are solutions of our system.
on the constraint defined by the Nehari manifold, which are solutions of our system.
Let ![]() be positive number such that
be positive number such that
![]()
where![]() .
.
Now we can state our main results.
Theorem 1. Assume that![]() ,
, ![]() ,
, ![]() , (F) satisfied and
, (F) satisfied and ![]() verifying
verifying![]() , then the system
, then the system ![]() has at least one positive solution.
has at least one positive solution.
Theorem 2. In addition to the assumptions of the Theorem 1, if (H) hold and ![]() satisfying
satisfying![]() , then
, then ![]() has at least two positive solutions.
has at least two positive solutions.
Theorem 3. In addition to the assumptions of the Theorem 2, assuming![]() , there exists a positive real
, there exists a positive real ![]() such that, if
such that, if ![]() satisfy
satisfy![]() , then
, then ![]() has at least two positive solution and two opposite solutions.
has at least two positive solution and two opposite solutions.
This paper is organized as follows. In Section 2, we give some preliminaries. Sections 3 and 4 are devoted to the proofs of Theorems 1 and 2. In the last Section, we prove the Theorem 3.
2. Preliminaries
Definition 1. Let![]() , E a Banach space and
, E a Banach space and![]() .
.
i) ![]() is a Palais-Smale sequence at level c ( in short
is a Palais-Smale sequence at level c ( in short![]() ) in E for I if
) in E for I if
![]()
where ![]() tends to 0 as n goes at infinity.
tends to 0 as n goes at infinity.
ii) We say that I satisfies the ![]() condition if any
condition if any ![]() sequence in E for I has a convergent sub- sequence.
sequence in E for I has a convergent sub- sequence.
Lemma 1. Let X Banach space, and ![]() verifying the Palais-Smale condition. Suppose that
verifying the Palais-Smale condition. Suppose that ![]() and that:
and that:
i) there exist![]() ,
, ![]() such that if
such that if![]() , then
, then![]() ;
;
ii) there exist ![]() such that
such that ![]() and
and![]() ;
;
let ![]() where
where
![]()
then c is critical value of J such that![]() .
.
Nehari Manifold
It is well known that J is of class ![]() in
in ![]() and the solutions of
and the solutions of ![]() are the critical points of J which is not bounded below on
are the critical points of J which is not bounded below on![]() . Consider the following Nehari manifold
. Consider the following Nehari manifold
![]()
Thus, ![]() if and only if
if and only if
![]() (2.1)
(2.1)
Note that ![]() contains every nontrivial solution of the problem
contains every nontrivial solution of the problem![]() . Moreover, we have the following results.
. Moreover, we have the following results.
Lemma 2. J is coercive and bounded from below on![]() .
.
Proof. If![]() , then by (2.1) and the Hölder inequality, we deduce that
, then by (2.1) and the Hölder inequality, we deduce that
![]() (2.2)
(2.2)
Thus, J is coercive and bounded from below on![]() .
.
Define
![]()
Then, for ![]()
![]() (2.3)
(2.3)
Now, we split ![]() in three parts:
in three parts:
![]()
![]()
![]()
We have the following results.
Lemma 3. Suppose that ![]() is a local minimizer for J on
is a local minimizer for J on![]() . Then, if
. Then, if![]() ,
, ![]() is a critical point of J.
is a critical point of J.
Proof. If ![]() is a local minimizer for J on
is a local minimizer for J on![]() , then
, then ![]() is a solution of the optimization problem
is a solution of the optimization problem
![]()
Hence, there exists a Lagrange multipliers ![]() such that
such that
![]()
Thus,
![]()
But![]() , since
, since![]() . Hence
. Hence![]() . This completes the proof.
. This completes the proof.
Lemma 4. There exists a positive number ![]() such that for all
such that for all![]() , verifying
, verifying
![]()
we have![]() .
.
Proof. Let us reason by contradiction.
Suppose ![]() such that
such that![]() . Then, by (2.3) and for
. Then, by (2.3) and for![]() , we have
, we have
![]() (2.4)
(2.4)
Moreover, by the Hölder inequality and the Sobolev embedding theorem, we obtain
![]() (2.5)
(2.5)
and
![]() (2.6)
(2.6)
From (2.5) and (2.6), we obtain![]() , which contradicts an hypothesis.
, which contradicts an hypothesis.
Thus![]() . Define
. Define
![]()
For the sequel, we need the following Lemma.
Lemma 5.
i) For all ![]() such that
such that![]() , one has
, one has![]() .
.
ii) For all ![]() such that
such that![]() , one has
, one has
![]()
Proof. i) Let![]() . By (2.3), we have
. By (2.3), we have
![]()
and so
![]()
We conclude that![]() .
.
ii) Let![]() . By (2.3), we get
. By (2.3), we get
![]()
Moreover, by (H) and Sobolev embedding theorem, we have
![]()
This implies
![]() (2.7)
(2.7)
By (2.2), we get
![]()
Thus, for all ![]() such that
such that![]() , we have
, we have![]() .
.
For each ![]() with
with![]() , we write
, we write
![]()
Lemma 6. Let ![]() real parameters such that
real parameters such that![]() . For each
. For each ![]() with
with![]() , one has the following:
, one has the following:
i) If![]() , then there exists a unique
, then there exists a unique ![]() such that
such that ![]() and
and
![]()
ii) If![]() , then there exist unique
, then there exist unique ![]() and
and ![]() such that
such that![]() ,
, ![]() ,
, ![]() ,
,
![]()
Proof. With minor modifications, we refer to [12] .
Proposition 1 (see [12] )
i) For all ![]() such that
such that![]() , there exists a
, there exists a ![]() sequence in
sequence in![]() .
.
ii) For all ![]() such that
such that![]() , there exists a a
, there exists a a ![]() sequence in
sequence in![]() .
.
3. Proof of Theorems 1
Now, taking as a starting point the work of Tarantello [13] , we establish the existence of a local minimum for J on![]() .
.
Proposition 2. For all ![]() such that
such that![]() , the functional J has a minimizer
, the functional J has a minimizer ![]() and it satisfies:
and it satisfies:
i) ![]()
ii) ![]() is a nontrivial solution of
is a nontrivial solution of![]() .
.
Proof. If![]() , then by Proposition 1 (i) there exists a
, then by Proposition 1 (i) there exists a ![]()
![]() sequence in
sequence in![]() , thus it bounded by Lemma 2. Then, there exists
, thus it bounded by Lemma 2. Then, there exists ![]() and we can extract a subsequence which will denoted by
and we can extract a subsequence which will denoted by ![]() such that
such that
![]() (3.1)
(3.1)
Thus, by (3.1), ![]() is a weak nontrivial solution of
is a weak nontrivial solution of![]() . Now, we show that
. Now, we show that ![]() converges to
converges to ![]() strongly in
strongly in![]() . Suppose otherwise. By the lower semi-continuity of the norm, then either
. Suppose otherwise. By the lower semi-continuity of the norm, then either ![]() and we obtain
and we obtain
![]()
We get a contradiction. Therefore, ![]() converge to
converge to ![]() strongly in
strongly in![]() . Moreover, we have
. Moreover, we have![]() . If not, then by Lemma 6, there are two numbers
. If not, then by Lemma 6, there are two numbers ![]() and
and![]() , uniquely defined so that
, uniquely defined so that ![]() and
and![]() . In particular, we have
. In particular, we have![]() . Since
. Since
![]()
there exists ![]() such that
such that![]() . By Lemma 6, we get
. By Lemma 6, we get
![]()
which contradicts the fact that![]() . Since
. Since ![]() and
and![]() , then by Lemma 3, we may assume that
, then by Lemma 3, we may assume that ![]() is a nontrivial nonnegative solution of
is a nontrivial nonnegative solution of![]() . By the Harnack inequality, we conclude that
. By the Harnack inequality, we conclude that ![]() and
and![]() , see for exanmple [14] .
, see for exanmple [14] .
4. Proof of Theorem 2
Next, we establish the existence of a local minimum for J on![]() . For this, we require the following Lemma.
. For this, we require the following Lemma.
Lemma 7. For all ![]() such that
such that![]() , the functional J has a minimizer
, the functional J has a minimizer ![]() in
in ![]() and it satisfies:
and it satisfies:
i) ![]()
ii) ![]() is a nontrivial solution of
is a nontrivial solution of ![]() in
in![]() .
.
Proof. If![]() , then by Proposition 1 ii) there exists a
, then by Proposition 1 ii) there exists a![]() ,
, ![]() sequence in
sequence in![]() , thus it bounded by Lemma 2. Then, there exists
, thus it bounded by Lemma 2. Then, there exists ![]() and we can extract a subsequence which will denoted by
and we can extract a subsequence which will denoted by ![]() such that
such that
![]()
![]()
![]()
![]()
This implies
![]()
Moreover, by (H) and (2.3) we obtain
![]() (4.1)
(4.1)
where,![]() . By (2.5) and (4.1) there exists a positive number
. By (2.5) and (4.1) there exists a positive number
![]()
such that
![]() (4.2)
(4.2)
This implies that
![]()
Now, we prove that ![]() converges to
converges to ![]() strongly in
strongly in![]() . Suppose otherwise. Then, either
. Suppose otherwise. Then, either ![]() . By Lemma 6 there is a unique
. By Lemma 6 there is a unique ![]() such that
such that![]() . Since
. Since
![]()
we have
![]()
and this is a contradiction. Hence,
![]()
Thus,
![]()
Since ![]() and
and![]() , then by (4.2) and Lemma 3, we may assume that
, then by (4.2) and Lemma 3, we may assume that ![]() is a nontrivial nonnegative solution of
is a nontrivial nonnegative solution of![]() . By the maximum principle, we conclude that
. By the maximum principle, we conclude that![]() .
.
Now, we complete the proof of Theorem 2. By Propositions 2 and Lemma 7, we obtain that ![]() has two positive solutions
has two positive solutions ![]() and
and![]() . Since
. Since![]() , this implies that
, this implies that ![]() and
and ![]() are distinct.
are distinct.
5. Proof of Theorem 3
In this section, we consider the following Nehari submanifold of ![]()
![]()
Thus, ![]() if and only if
if and only if
![]()
Firsly, we need the following Lemmas
Lemma 8. Under the hypothesis of theorem 3, there exist![]() ,
, ![]() such that
such that ![]() is nonempty for any
is nonempty for any ![]() and
and![]() .
.
Proof. Fix ![]() and let
and let
![]()
Clearly ![]() and
and ![]() as
as![]() . Moreover, we have
. Moreover, we have
![]()
If ![]() for
for![]() ,
, ![]() for
for ![]() , then there exists
, then there exists
![]()
where
![]()
and
![]()
and there exists ![]() such that
such that![]() . Thus,
. Thus, ![]() and
and ![]() is nonempty for any
is nonempty for any![]() .
.
Lemma 9. There exist M, ![]() positive reals such that
positive reals such that
![]()
and any ![]() verifying
verifying
![]()
Proof. Let![]() , then by (2.1), (2.3) and the Holder inequality, allows us to write
, then by (2.1), (2.3) and the Holder inequality, allows us to write
![]()
where![]() . Thus, if
. Thus, if
![]()
and choosing ![]() with
with ![]() defined in Lemma 8, then we obtain that
defined in Lemma 8, then we obtain that
![]() (5.1)
(5.1)
Lemma 10. Suppose ![]() and
and![]() . Then, there exist r and
. Then, there exist r and ![]() posi- tive constants such that
posi- tive constants such that
i) we have
![]()
ii) there exists ![]() when
when![]() , with
, with![]() , such that
, such that![]() .
.
Proof. We can suppose that the minima of J are realized by ![]() and
and![]() . The geometric conditions of the mountain pass theorem are satisfied. Indeed, we have
. The geometric conditions of the mountain pass theorem are satisfied. Indeed, we have
i) By (2.3), (5.1) and the fact that![]() , we get
, we get
![]()
Exploiting the function ![]() and if
and if![]() , we obtain that
, we obtain that ![]() for
for![]() . Thus, there exist
. Thus, there exist![]() ,
, ![]() such that
such that
![]()
ii) Let![]() , then we have for all
, then we have for all ![]()
![]()
Letting ![]() for t large enough. Since
for t large enough. Since
![]()
we obtain![]() . For t large enough we can ensure
. For t large enough we can ensure![]() .
.
Let ![]() and c defined by
and c defined by
![]()
and
![]()
Proof of Theorem 3.
If
![]()
then, by the Lemmas 2 and Proposition 1 ii), J verifying the Palais-Smale condition in![]() . Moreover, from the Lemmas 3, 9 and 10, there exists
. Moreover, from the Lemmas 3, 9 and 10, there exists ![]() such that
such that
![]()
Thus ![]() is the third solution of our system such that
is the third solution of our system such that ![]() and
and![]() . Since
. Since ![]() is odd with res- pect u, we obtain that
is odd with res- pect u, we obtain that ![]() is also a solution of
is also a solution of![]() .
.