1. Introduction
In Consilience [1] (p. 181), the author points out that: “People expect from the Social Sciences … the knowledge to understand their lives and control their future”. Regarding Economics, it seems that we are far away from this goal according to the XXth century events. Anyway, it is our understanding that in order to advance in Social Sciences and provide useful knowledge and information to society, economic theories have to search for new concepts and possibly new models stemming from another areas of knowledge. In Economics, there has not been still established, the relationship between individuals behaviour or the laws of the particular (Microeconomics) and the aggregated data (Macroeconomics). Consilience is precisely this capacity i.e. the ability to link aggregated data with the finer details below. Complexity can bring theories and models that can be used in economics, with a double purpose: making better forecasts and gaining knowledge of how to build theories. The same author comments: “Complexity theory needs more empirical information” [1] (p. 90). As time goes on and our capacity to gather data augments, we have better economics empirical data we can use either to check new models or to expand them.
In a previous paper, [2] have attempted to set up a link between a rule of thumb used in Economics and a weak chaos model. We refer in particular to the Taylor Rule and the Sandpile model. Recent studies in Economics have brought new data and we are going to review our findings in the light of them.
In the following sections, we do present new findings regarding the last US Housing Bubble reinforcing the assumption of our original paper, that is, that models as the sandpile, can be used as a suggestive line of research in Economics. For that to be achieved, there are several requisites to be met. First is the presence of punctual and violent behaviour like bursts known as avalanches. The narrative describing them for the US Housing Bubble matches the wording in our former paper. Second, a triggering fact is needed for avalanches to occur, as is the violation of a critical condition, clearly identified for the US Housing Bubble and third, a Power Law statistic. This last one is an issue still pending of a clear definition, because there must be a common accepted measure of the crisis, and also due to the scale of the problem (there are not long GDP series). To avoid this weakness, we have considered two outcomes, one is that by means of the generality principle, we can use an example of other market activity, and as second choice one that pop’s up a subject of great interest for the matter. It is the concept of “punctuated equilibrium” [3] widely used in Biology by which, in a nutshell, Evolution proceeds in bursts after long periods of stasis. Evidence widely supports this idea and the presence or not of a robust statistic is not relevant, instead the relative frequencies are of value. We can wonder how to move the idea of punctuated equilibrium to the realm of Economics. Quite simple, check economic history. After every big economic burst or crisis, important changes took place everywhere, improving economies to be trustful though being much more bigger and complex, and what is more important, the world is a wealthier place after that happened. This is a topic worth to analyze deeper in the future.
As a concluding remark: “Any theory with a claim of novelty must enlighten old problems and suggest extensions” [3] and this is our goal when using the sandpile model in Economy.
2. The Sandpile Model
Weak chaos models such as the sandpile are suitable as long as the system under study presents some well known traits or characteristics [4] and [5] we refer to that literature for a complete account of the model. First there is a set of working rules that we use to describe the behaviour or dynamics of the model. There is a building rule or how the pile grows and stock more material and also a relaxing or dissipating rule as a toppling rule that works out when adding items to the pile a critical condition is overcome. Avalanches is the intuitive name associated to that event. The size n of an avalanche is an amount associated to the number of times n the toppling rule is used when is triggered. The second element is a critical condition that when overcome triggers an avalanche and is described by the rules set up in the model. And the third element is that the system under study presents a statistic of behaviour linking the size n of an avalanche to their likeliness P(n) that can be described by the Power Law (PL) distribution 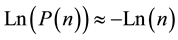 where P(n) is the probability of an avalanche of size n.
where P(n) is the probability of an avalanche of size n.
Should it be worth noting that, the sandpile model is contingent and second that there is not any relationship between the inner working of the pile and the observed behaviour.
3. The Findings
In our paper we set up a loose relationship between the Taylor Rule and the Sandpile with the evidence available, but recently a new book brought more material to be considered. This is not the place to comment the book but it is the place where to set the matter in perspective. The book [6] is a deep, long and documented study of the housing bubbles plenty of useful comments for our purpose. In this respect there are some salient findings of interest in order to reinforce the hypothesis of our former paper.
About the causes or how the critical condition is violated, these authors say:
“...Federal Reserve intervention in the market for Treasury securities has been used as the principal monetary policy instrument... We show that these interventions which alter the short-term interest rates had their primary impact on residential mortgage lending until the Great Recession”.
(Ibid in Conclusions)
and also add:
“Although bubbles are not fundamentally caused or driven only by external circumstances we first identify several promising ‘triggers’ in both the public and private sectors that either after coincided or preceded the 1997 take off as an ‘incubation interval’. These events or developments included the Bipartisan Taxpayer Relief Act of 1997 Act that exempted home resales from capital gains up to $500,000. Both the timing and the incentive provided for the diversion of capital investment into homes combined to make it a primer trigger suspect. Incentives matter and the problem with the Act is the differential treatment of houses relative to productive capital investments, channeling savings and borrowings into house consumption”.
(Ibid section 11.8 Triggers)
That is, the authors indicate that the FED’s intervention on the monetary policy and facilitating capital investment were causes of the US housing bubble. As we pointed out [2] in our previous paper, the simultaneous action on both variables the rate of interest (r) and liquidity (L) counter sense via the relationship:

results in a conflict driving the system to instability.
Regarding the avalanches they say:
“…when the bubble collapse... It can be compared to an avalanche or earthquake: Pressure builds invisible to our perception and it is difficult to predict the timing of its dramatic release but we can search for characteristic features that precede and follow the event and we can also take precautions that mitigate damage when event occurs”.
(Ibid p. 21)
There are no better words in our opinion to describe an avalanche, and the hidden inner working of the pile.
4. Missing Points
In order to establish a reasonable parallelism between the US Housing Bubble and the sandpile, two facts that characterize the sandpile model as the process of avalanches, and a critical condition both have been clearly documented. Anyway we are still pending either of identifying the third and decisive fact, that is, to have a stat of events, confirming that economic bubbles, are properly described by a Power Law distribution or alternatively to view the new data as part of a ‘punctuated equilibrium’ approach.
By the time being we do not count neither, with information regarding the size of the economic crisis as measured by the variation of GDP, should that criteria be generally accepted, nor with a long series of this data. But we can proceed to study, according to the principle of generality, another phenomena in the same field of theory i.e. economics. We have seen in ecology [7] and geology [8] [9] descriptions of local processes governed by laws, as is the Power Law. In complex phenomena we are not able to describe the detailed behaviour of the components, but the averages or the global behaviour, see for example the Belousov Zhabotinisky Model where complex behaviour showing patterns is displayed in a fluid under a chemical reaction. There are several other cases to illustrate our purpose. In Reference [10] Benoit Mandelbrot while studying the fractal structure of the irregular behaviour of stock price changes in the NY Stock exchange saw a graphic with the values of the Nile level (Noah and Joseph’s effect). There he recognized the visual similarity of this process with the fractal behaviour, and used it to forecast the size of the Nile’s flooding, as he did. Also Fibonnaci numbers serve to study the offspring of bees and the sunflower structure and similarly other conceptual and abstract structures bring new light into science. Why not Power Law could be the fingerprint of some economic problems? Self organization, emergence and bifurcations are visible traits or characteristics that we can find in the behaviour of a complex system that are common to the Economy, and the PL is one of the checks. By other side the issue of the US Housing Bubble as part of a wider universe, say the financial and goods markets, could be a clear manifestation of ‘punctuated equilibrium’ of a evolutionary process, where advances are prompted by bursts with long periods of stasis in between, measured in economic time of scale. This way there would be not the need of a Power Law distribution to be checked, because ‘punctuated equilibrium claims about relative frequency, non exclusivity’ [3] . Intuitively we can share that most of the activity of the economic system as measured by the GDP change is normal (stasis) with bursts we call recessions.
Anyway we have searched the economic literature and found a case worth to examine. It is a market, with long history in terms of data and relatively recent. It is the market related to the trading day in the Ten-Year Treasury Bonds [11] .
As indicated [11] (p. 88) they have analyzed price changes during 25 years (May 1978-May 2004) and found that:
“Roughly 0.75 percent of the Treasury bond price changes in the sample are greater in absolute value than 3.5 standard deviations, more than 16 times the number of such outliers that would be expected from a normal distribution of price changes. Let me repeat―there are 16 times more price changes in excess of 3.5 standard deviations than expected with the normal distribution. Assuming 250 trading days in a year, on average bond price changes of this or greater magnitude in absolute value occur twice per year instead of once every 8 years. The normal distribution provides a grossly misleading picture of the risk of large price changes. Really large changes of 4.5 or more standard deviations―the ones that can break a highly leveraged company―occur only 7 times in a million under the normal distribution, but there are 11 such changes in the 6573 daily observations...”
Then if we try to adjust a potential distribution like:

We can do that and obtain for the second instance that is 11 changes greater than 4.5 standard deviations in 6573 observations a λ equal to 0.144 and that means that it should exists more than 29 cases of the standard deviations greater than 3.5 times. The paper indicates that there was 0.75% of the cases with a value greater than 3.5 standard deviations what means 49 cases―the normal distribution was assuming 3―and the Power Law 29. We should do that using the first instance, that is for values greater than 3.5 standard deviations, we would obtain 18 instances of values greater than 3.5 standard deviations. The sample provides just 11. The best fit is in between both values of λ calculated for 3.5 and 4.5 standard deviations, as usual.
It is not decisive but at least interesting.
5. Summary
The recorded facts of the US Housing Bubble allow us to interpret that process in terms of the sandpile and/or punctuated equilibrium. The narrative of the bust of the US Housing Bubble is astonishingly similar to the sandpile as we described it, and also a triggering fact has been documented. Anyway it is difficult to complete the task presenting a Power Law statistic linking the size and frequency of avalanches as in the sandpile, characterizing the US Housing Bubble. We went around this weakness and selected another market as an example of the generality principle, and checked if that could be case, with a better result than the obtained by means of the standard normal distribution.
Anyway, there is another alternative to that. We can set up a parallelism with Biology, Ecology and Seismology in order the Economy to present “punctuated equilibrium” phenomenon due to the shared behaviour with Natural disciplines, where in absence of good information to build a stat, the relative frequency can be a finer measure. This matter needs further clarification, by having more experimental facts to check.
Acknowledgements
Visiting Professor at the Faculty of Economics and International Studies at the University of Buckingham Dr. Pedro Schwartz Girón was very helpful providing source materials for this paper.