1. Introduction
The notion of synchronization is well known from the viewpoint of classical mechanics since early 16th century. Since then, many other examples have been reported in the literature. However, the possibility of synchronizing chaotic systems is not so intuitive, since these systems are very sensitive to small perturbations on the initial conditions and, therefore, close orbits of the system quickly become un-correlated. Surprisingly, in 1990 it was shown that certain subsystems of chaotic systems can be synchronized by linking them with common signals [1] . In particular, the author reported the synchronization of two identical (i.e., two copies of the same system with the same parameter values) chaotic systems. They also show that, as the differences between those system parameters increase, synchronization is lost. Subsequent works showed that synchronization of non-identical chaotic systems is also possible. Many fundamental characteristics can be found in a chaotic system, such as excessive sensitivity to initial conditions, broad spectrum of Fourier transform, and fractal properties of the motion in phase space. Due to its powerful applications, both control and synchronization problems have extensively been studied in the past decades for chaotic systems such as Lorenz system [2] -[5] , Chua’s system [6] , Rossler system [7] , Chen system [8] , Lu system etc. [9] [10] . In fact, the state trajectories of chaotic systems evolve in a strange attractor. In addition, there are several control methods for chaotic systems which have extensively been studied in the literature, such as linear state error [11] , impulsive control [12] , adaptive control [13] , fuzzy model [14] , sliding mode control design [15] [16] , Robust chaos suppression [17] , etc.
However, some noises or disturbances always exist in the physical systems that may cause systems instability and thereby destroying the stability performance. Therefore, the problem that how to reduce the effect of the noise or disturbances in chaotic systems becomes an important issue.
This paper can be summarized as follows: In the next section, we introduce notion of chaos synchronization and propose some theorems for chaos synchronization based upon the analysis of nonlinear dynamical systems. In Section 3, we explain proposed theorems in terms of chaotic Lorenz system. Numerical simulations are given to verify proposed theorems in Section 4.
2. Chaos Synchronization
Given two systems
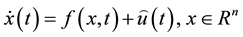 (1)
(1)
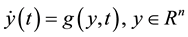 (2)
(2)
with 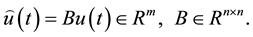 The problem consists of choosing an appropriate controller
The problem consists of choosing an appropriate controller 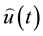 in such a way as to have
in such a way as to have
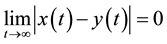 (3)
(3)
Equations (1), (2) and (3) can describe both the problems of controlling and synchronizing a chaotic system. If the reference (2) is chosen to a chaotic system, identical to (1), starting from different initial condition, (3) describes a synchronization problem while if the reference model evolves along a periodic orbit a chaos control problem is described.
To explain the synchronization of (1) and (2), the error equation is formed
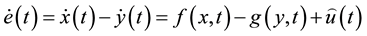 (4)
(4)
An orthogonal projection operator 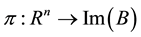 is found so that (4) could be rewritten as
is found so that (4) could be rewritten as
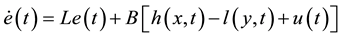 (5)
(5)
where 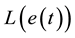 is the projection of
is the projection of 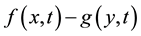 on the complementary space of Im(B), which is assumed to be linear, and
on the complementary space of Im(B), which is assumed to be linear, and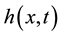 ,
, 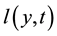 are the projection on Im(B) of
are the projection on Im(B) of 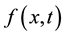 and
and 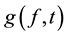 respectively. Our aim is to find
respectively. Our aim is to find 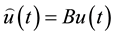 such that (1) synchronizes with (2) and the error equation stabilize and become regular.
such that (1) synchronizes with (2) and the error equation stabilize and become regular.
M. D. Bernardo [18] proposed a modified adaptive approach in which for a given matrix 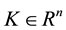 such that
such that ![]() is a Hurwitz matrix, that is all its eigenvalues are in the left half of the complex plane, we solve the Lyapunov equation
is a Hurwitz matrix, that is all its eigenvalues are in the left half of the complex plane, we solve the Lyapunov equation
![]() (6)
(6)
Theorem 1. [18] Let ![]() be the positive definite solution of (6) and let
be the positive definite solution of (6) and let![]() . The con- troller
. The con- troller ![]() guarantees that for every initial condition
guarantees that for every initial condition
![]() : 1), 2).
: 1), 2).
In Theorem 1, ![]() is adaptively estimated according to the law
is adaptively estimated according to the law ![]() where
where ![]() is a continuous function such that
is a continuous function such that![]() ,
,![]() . We can decompose
. We can decompose ![]() as
as ![]() .
.
Assumption 1: The projection of ![]() on the complementary space of Im(B) is linear, that is for some linear matrix L:
on the complementary space of Im(B) is linear, that is for some linear matrix L:
![]() (7)
(7)
Under assumption 1, (4) becomes
![]() (8)
(8)
We wish, now, to choose an appropriate function ![]() in order to solve the problem stated in (1). If we recall one of the main properties of feedback K, namely, the feedback linearization, we can try to achieve the control by linearizing the systems involved via a combined feedback plus feedforward action. Under assumption 1 we can trivially prove that:
in order to solve the problem stated in (1). If we recall one of the main properties of feedback K, namely, the feedback linearization, we can try to achieve the control by linearizing the systems involved via a combined feedback plus feedforward action. Under assumption 1 we can trivially prove that:
Theorem 2. [19] If (L, B) is stabilizable then ![]() with
with
![]() (9)
(9)
where ![]() is such that all eigenvalues of (L - BK) are in the left hand side of the complex plane will ensure (3).
is such that all eigenvalues of (L - BK) are in the left hand side of the complex plane will ensure (3).
It is difficult to provide the controller with a perfect knowledge of the function g but instead assume only that its projection l is bounded by a known continuous function ![]() in the following sense:
in the following sense:
Assumption 2:![]() ,
, ![]() With
With ![]() continuous.
continuous.
To exploit the fact that the system ![]() is a chaotic system evolving either on a strange attractor or on a periodic orbit/equilibrium point, to deduce that its solution must be bounded for all t. hence, for some known M, we assume
is a chaotic system evolving either on a strange attractor or on a periodic orbit/equilibrium point, to deduce that its solution must be bounded for all t. hence, for some known M, we assume
![]()
It then follows by assumption 2 that there exists ![]() such that
such that
![]() (10)
(10)
The idea is to exploit this property of the reference model, in order to achieve the control. In so doing so we consider a controller of the form
![]() (11)
(11)
Hence we still have a linear term −ke and a feedback linearization term![]() , but the feed forward, responsible of the compensation of
, but the feed forward, responsible of the compensation of ![]() has disappeared. What we have now is a discontinuous term depending upon the known bound W, which will dominate the nonlinearity of the reference model and therefore should guarantee the desired goal. In fact, the hypothesis of Theorem 2 and (10) yield the following.
has disappeared. What we have now is a discontinuous term depending upon the known bound W, which will dominate the nonlinearity of the reference model and therefore should guarantee the desired goal. In fact, the hypothesis of Theorem 2 and (10) yield the following.
Theorem 3. [19] Let ![]() be the positive definite matrix solution of the Lyapunov equation
be the positive definite matrix solution of the Lyapunov equation ![]() with
with![]() .Define the set valued mapping
.Define the set valued mapping ![]() such that
such that
![]() (12)
(12)
With B(1) denoting a closed ball of radius one in![]() , and embed the feedback controlled error system (8) in the differential equation inclusion
, and embed the feedback controlled error system (8) in the differential equation inclusion
![]() (13)
(13)
Then the origin is asymptotical stable for the error system (8).
Proof: Note that ![]() is upper semi continuous on
is upper semi continuous on![]() , with non-empty, convex and compact value. Therefore, for each
, with non-empty, convex and compact value. Therefore, for each![]() , the system (8) with
, the system (8) with ![]() has a maximal solution
has a maximal solution![]() . Let
. Let![]() . Obviously:
. Obviously:![]() ,
, ![]() ,
, ![]() and for all
and for all ![]()
![]()
Let ![]() be a maximal solution, then
be a maximal solution, then![]() , for almost all t and we may deduce that the error decays asymptotically to zero. Thus the proof of the Theorem 3 is complete.
, for almost all t and we may deduce that the error decays asymptotically to zero. Thus the proof of the Theorem 3 is complete.
Assumption 3: In order to find a sufficient synchronization criterion the following assumption on the drive system is needed. This assumption is in the light of the drive system being free and chaotic and based on a well-known fact that chaotic attractors are bounded in phase space
For any bounded initial state x0 within the defined domain of the drive system, there exist some finite real constants ![]() such that
such that
![]()
Keeping in view these facts we obtain the following theorem followed by a lemma which seems to be very significant to develop the subject of chaos theory.
Lemma 1: If system (1) involves r chaos terms in its dynamics, then control vector ![]() can be chosen such that
can be chosen such that
![]() ,
,
![]() ,
,
and![]() ,
, ![]()
Theorem 4. System (1) will synchronize with response (2) if control gain matrix B is chosen such that error dynamics of drive-response given by
![]() (14)
(14)
is asymptotically stable provided the choice of positive Lyapunov function ![]() for the stabilization of (14) imply the derivative
for the stabilization of (14) imply the derivative ![]() is negative definite.
is negative definite.
Proof: Using lemma 3.1 Equation (14) can be re-written as
![]()
Now choosing the positive definite Lyapunov function
![]() (15)
(15)
![]()
Equation (15) in matrix notation can be written as
![]() (16)
(16)
where
![]()
is positive definite for certain values of ![]() and
and![]() .
.
Now the derivative ![]() is given by
is given by
![]() (17)
(17)
On solving Equation (17) using (14) we find a polynomial of the following form
![]() (18)
(18)
where![]() ,
, ![]() and
and ![]() are functions of t only.
are functions of t only.
By excluding less important terms we get desired negative definite polynomial i.e.
![]() (19)
(19)
where
![]()
is negative definite for certain values of ![]() and
and![]() . Proof of the Theorem 4 is complete.
. Proof of the Theorem 4 is complete.
3. Synchronization of Two Lorenz Systems
The Lorenz system described by the following system of non linear differential equations
![]()
For the parameter values ![]() has a chaotic attractor portrayed in Figure 1.
has a chaotic attractor portrayed in Figure 1.
Now, consider the Lorenz chaotic system
![]() (20)
(20)
as a drive system and the response system given by
![]() (21)
(21)
where ![]() are unknown feedbacks controlling functions.
are unknown feedbacks controlling functions.
Now using![]() ,
, ![]() ,
, ![]() and
and![]() ,
, ![]() ,
, ![]() , error system becomes
, error system becomes
![]() (22)
(22)
Now we can re-state Theorem4 for Lorenz system as follows:
Theorem 5. System (20) will synchronize with response (21) if control gain matrix B is chosen such that error dynamics of drive-response given by (22) is asymptotically stable provided the choice of positive Lyapunov function ![]() for the stabilization of (22) imply the derivative
for the stabilization of (22) imply the derivative ![]() is negative definite.
is negative definite.
Proof: Using lemma 1 we take control functions as![]() ,
, ![]() ,
,![]() .
.
We choose Lyapunov function
![]() (23)
(23)
where![]() . Differentiating (23) with respect to t, we obtain
. Differentiating (23) with respect to t, we obtain
![]() (24)
(24)
Equation (24) is negative definite if the matrix
![]()
is negative definite. The following conditions must hold
1) ![]()
2) ![]()
3)![]() .
.
Proof of the Theorem 4 is complete.
4. Numerical Simulation
In this section we verify the control laws presented in the previous sections via numerical simulations. Keeping
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() fixed and choosing
fixed and choosing![]() ,
, ![]() ,
, ![]() according to proposed theorem one can obtain a number of values for which Lorenz system synchronized. For example if we choose a particular approximation for which
according to proposed theorem one can obtain a number of values for which Lorenz system synchronized. For example if we choose a particular approximation for which![]() ,
, ![]() ,
, ![]() and
and![]() ,
, ![]() ,
, ![]() ,
,
and![]() ,
, ![]() ,
, ![]() , for the chaotic drive and response Lorenz systems and
, for the chaotic drive and response Lorenz systems and![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , for the synchronized drive and response Lorenz systems then we can see an excellent agreement with the proposed theorems. Figures 2(a)-(d) are the trajectories of chaotic Lorenz system. Figures 2(e)-(h) are the synchronization between two identical Lorenz systems.
, for the synchronized drive and response Lorenz systems then we can see an excellent agreement with the proposed theorems. Figures 2(a)-(d) are the trajectories of chaotic Lorenz system. Figures 2(e)-(h) are the synchronization between two identical Lorenz systems.
5. Conclusion
We analyze chaotic dynamics of nonlinear systems and study chaos suppression. We extend our study up to chaos synchronization by discussing Pecora-Carroll and other methods available in literature. We proposed a theorem in general and another one for a particular case of Lorenz system. Numerical simulations are given to
verify the proposed criterion. In a particular approximation for which![]() ,
, ![]() ,
, ![]() and
and
![]() ,
, ![]() ,
, ![]() and
and![]() ,
, ![]() ,
, ![]() , for the chaotic drive and response Lorenz systems and
, for the chaotic drive and response Lorenz systems and![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , for the synchronized drive and response Lorenz systems then we show an excellent agreement with the proposed theorems.
, for the synchronized drive and response Lorenz systems then we show an excellent agreement with the proposed theorems.