Recent Advances in Global Optimization for Combinatorial Discrete Problems ()
1. Introduction
Global optimization is the task of finding the absolutely best set of admissible conditions to achieve an objective under given constraints, assuming that both are formulated in mathematical terms [1] . There exist many global optimization problems with discrete variables in engineering design, information science, and related fields. In such practical applications, some or all of the variables must be selected from a list of integer or discrete values. For example, structural members may have to be designed using sections available in standard sizes, member thicknesses may have to be selected from the commercially available ones, and the number of bolts for a connection must be an integer. The variables of optimization in these cases are not continuous [2] . One of the interesting discrete-variables global optimization problems is the optimization of Water Supply System WSS design. The complexity, nonlinearity and discrete nature of WSS optimization problems seriously limit the local search algorithms methodologies as they can be trapped in a local optima in the solution space “the set of all possible solutions” [3] . Evolutionary Algorithms EA have been widely popular nowadays in the global optimized design of WSS because it can deal easier with discrete problems, which permits, opposed to other optimization methods, the direct inclusion of commercial pipe diameters in the design, in addition to the fact that EA allow for a family of solutions, one can obtain various optimal solutions or solutions close to the optimal case [4] -[6] .
We present in this paper the WSS optimization as an example of combinatorial discrete optimization problems. The optimization algorithms used to solve this type of problem are divided into two categories the classical algorithms and the Evolutionary Algorithms EAs which are more popular. We highlight the main differences between the two categories, and then we concentrate on the last category. We demonstrate the mathematical basics of four EAs that have been used successfully to solve WSS optimization problems (Genetic Algorithms GAs, Particle Swarm Optimization PSO, Ant Colony Algorithm ACOA and Harmony Search HS). We adopt the real Genetic Algorithm, as it is one of the fundamental evolutionary algorithms and the most used nowadays. We compare the real GA as mathematical construction, results and efficiency with the three more-recent algorithms, taking the New-York City WSS as a case study.
2. Particularity of Water Supply System Optimization
The complexity of water supply systems comes from multiple pumps, valves and reservoirs, head losses, large variations in pressure values, several demand loads, etc. In such systems, finding the global optimal solution is a difficult task using the conventional trial and error methods, while the incomplete mathematics precisely, the innovative optimization algorithms are more widely explored in optimization process of the water supply systems [7] .
Design optimization problems in WSS are based on searching the system characteristics which minimise the total system cost without affecting the proper operation of the hydraulic system and the consumers supply. This means that the system must be economic and reliable. However, increase in reliability can imply higher costs [8] . The problem formulation required for the optimization of WSS is different from that used for other combinatorial optimization problems, such as the traveling salesman problem, in the way the problem is constrained. For example, in the traveling salesman problem, the only constraints are that each city must be visited once only and that the finishing point must be the same as the starting point. In this situation, tabu lists are used to ensure that only feasible solutions are generated [9] . However, the constraints that need to be satisfied in the optimal design of WSS are of a different nature. The feasibility of a particular trial solution e.g., whether minimum pressure constraints have been satisfied can only be assessed after it has been constructed in its entirety, and consequently, the constraints cannot be taken into account explicitly during the construction of trial solutions. In this way, the feasibility of the solutions can only be assessed after their full construction.
In most works dealing with optimization design of WSS, some benchmark networks have been constantly used for the comparison between distinct developed methodologies, from which we mention the New York City Tunnels firstly presented by Schaake and Lai 1969 [10] , and the Hanoi network in Vietnam [11] : 1) The New York City Tunnels problem consists essentially of a single source in Hill View and two main city tunnels. The objective of this problem is to determine the need of laying a new pipe parallel to the existing ones and also to determine their diameters. A unique demand case is considered. 2) The Hanoi network contains three loops and also ramifications. The objective of this problem is to find the least-cost diameters for all pipes while respecting the minimum value for the head pressure at each node. In this work, we take The New York City Tunnels problem as case study.
Problem Statement
As a common practice, due to the nature of WSS, one uses an objective function which only takes into account the pipeline costs and penalty costs, if not complying with minimal values for the pressure at each node of the network and the objective function can be written as follows [5] [6] [12] [13]
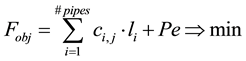 (1)
(1)
where i is the pipe number (1 ® i ® S, S is the number of all pipes i.e. the number of variables),  is the cost per meter depending on the diameter j of pipe i (1 ® j ® J, J is the number of available commercial diameters i.e. the number of options), li is the length of pipe i. The penalty Pe only applies when the pressure in any node is less than a predetermined minimal value. In order to reveal the feasible solutions only, the hydraulic simulations is required to check pressure constraints and to obtain the flow velocity in each pipe, and if the resulting velocity in one pipe is larger than the determined threshold velocity, this pipe diameter is increased to the next larger commercial size. Hydraulic simulators are coupled successfully with the optimization algorithms to evaluate each solution.
is the cost per meter depending on the diameter j of pipe i (1 ® j ® J, J is the number of available commercial diameters i.e. the number of options), li is the length of pipe i. The penalty Pe only applies when the pressure in any node is less than a predetermined minimal value. In order to reveal the feasible solutions only, the hydraulic simulations is required to check pressure constraints and to obtain the flow velocity in each pipe, and if the resulting velocity in one pipe is larger than the determined threshold velocity, this pipe diameter is increased to the next larger commercial size. Hydraulic simulators are coupled successfully with the optimization algorithms to evaluate each solution.
3. Classification of Optimization Algorithms
Global optimization algorithms can be distinguished according to two general classifications: 1) classical algorithms, based essentially on the computation of the objective function gradient and/or function evaluations and 2) Evolutionary /Meta-heuristic algorithms, consisting essentially on exploratory search and generally based on a phenomena that occur in nature or even based on artificial intelligence.
The classical algorithms used in Water Supply Systems as classified in [7] include: Linear Programming (LP), Nonlinear Programming (NLP), Integer Nonlinear Programming including MINLP (Mixed Integer NonLinear Programming) [14] and Dynamic Programming. These kinds of algorithms enable finding the position of an optimal solution with certain tolerance. They usually converge to local optimal solutions which could not be the global optimum. In addition, the need of derivative evaluations can, in some cases, complicate the optimization process. These classical methods of optimization involve the use of gradients or higher-order derivatives of the fitness function. However, they are not well-suited for many real-world problems since they are not able to process inaccurate, noisy, discrete and complex data [6] [15] [16] .
On the other hand, there are the incomplete mathematics presented by the Evolutionary /Meta-heuristic algorithms. These innovative techniques have shown great potential and good perspective for the solution of various optimization problems. Due to the exploratory nature of the heuristic algorithms, the probability of finding global optimal solutions using these advanced techniques is higher and they provide the advantages of not requiring derivatives calculations and not relying on the initial decision variables; but their main disadvantage is related to the higher computational effort [17] . However, Metamodels have proven be very useful when it comes to reduc- ing the computational requirements of Evolutionary Algorithm-based optimization by acting as quick-solving surrogates for slow-solving fitness functions [18] . As a common example of these metamodels, we cite the Artificial Neural Networks (ANNs) due to their demonstrated ability to model water quality variables in distribution systems [19] -[21] . In addition, many researches have focused recently on the amelioration of computational efficiency of evolutionary algorithms, as the work of Montalvo et al., 2010 [6] on Particle Swarm Optimization PSO with self-adaptive parameters, the work of Bi et al. 2015 [22] on Improved genetic algorithm optimization by incorporating domain knowledge and the work of Beheshti and Shamsuddin 2015 [23] on Non-parametric PSO that enhances the global exploration and the local exploitation in PSO without tuning any algorithmic parameter while solving global optimization problems.
Likewise, evolutionary algorithms are usually the most used for solving multi-objectives problems. They deal with a set of solutions during the search procedure, allowing to obtain a set of optimal solutions in a single run, while the classic complete methods only lead to a single solution and cannot guarantee the generation of different points based on the optimal global solution.
4. Mathematical Basics of Some (EAs) Used in WSS Discrete Problem
Evolutionary algorithms (EAs) have shown considerable success in solving global optimization problems; thus, it has attracted much attention in the past few years. Recently, a large number of EAs, such as genetic algorithms (GAs), particle swarm optimization (PSO), Ant Colony Algorithm (ACOA) and Harmony Search (HS) have been proposed.
Here in, we state the most promising incomplete mathematics algorithms used in solving global optimization problems such as the water supply systems:
4.1. Genetic Algorithms (GA)
From the group of heuristic algorithms, it is usual to find works mostly applying the (GA). The theory behind GAs was proposed by Holland (1975) [24] and further developed by Goldberg (1989) [25] and others in the 1980s and 1990s.
There are many variations of GAs, but the following general description encompasses most of the important features. The analogy with nature requires creation by computer of a set of solutions called a population. Each individual in a population is represented by a set of parameter values that completely propose a solution. These are encoded into chromosomes, which are originally sets of character strings, analogous to the chromosome found in DNA. The GA search, sometimes with modification, has been proven to perform efficiently in a large number of applications. The selection of an appropriate chromosome representation of candidate solutions to the problem at hand is the foundation for the application of genetic algorithms to a specific problem. With a sufficiently large population of chromosomes, adequate representation will be achieved.
The typical size of the population for a GA can range from 30 to 1000. In addition, GAs use probabilistic (not deterministic) transition rules, and they also use objective function information, not derivatives or other auxiliary knowledge [25] .
In the WSS optimization problem, every pipe diameter is considered like a gene that has as many options as the available commercial diameters, while the whole network is considered as the chromosome “individual” that should “fit” to the environment presented by the objective function and the survival chances for the possible solutions or individuals in the population are bigger for those who propose the least cost (Figure 1). Detailed explanations of the notations of the reproduction, crossover and mutation operators using real representation can be seen in [4] .
Returning to the objective function in Equation (1), the penalty is applied when infeasible solutions, failed to meet the minimum nodal pressure requirements. This pressure is 30 m above ground level in the case of New-York city WSS. However, the infeasible solutions are not removed from the population. Instead they are allowed to join the population and help guide the search, but with penalty term incorporated in objective function. The penalty activation reduces the strength of the infeasible solution relative to other solutions in the population consequently leading to the degradation of its fitness. The penalty is a function of the distance from feasibility. The bigger the difference between the nodal pressure and the required nodal pressure, the greater the penalty is. The maximum violation of the pressure constraint is multiplied by the penalty multiplier Pm, which is a function of the generation number, which allows a gradual increase in the penalty term:
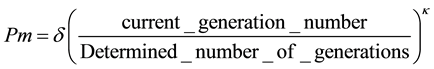 (2)
(2)
The penalty multiplier Pm should be a value that does not allow the best infeasible solution to be better than any feasible solution in the population. As we note from Equation (2), when the generation number approaches the maximum determined number of generations Gmax, the penalty value increases. The selected appropriate values of κ and δ in Equation (2) are 0.8 and 100,000 respectively.
The application of real GA on the New-York network, hereafter, gives more details about the method with comparison to other evolutionary algorithms.
![]()
Figure 1. Flow-chart for the GA implementation with the related action.
4.2. Particle Swarm Optimization (PSO)
PSO is a relatively new category of stochastic, population-based optimization algorithms that draw inspiration from the collective behavior and emergent intelligence that arise in socially organized populations. Within the PSO algorithm, every solution is a bird of the flock and is referred to as a particle: in this framework the birds, besides having individual intelligence, also develop some social behavior and coordinate their movement towards a destination [26] .
For nodes with pressures larger than this minimal value, the associated individual penalties vanish, and one uses the usual Heaviside step function H in the explicit expression for Pe:
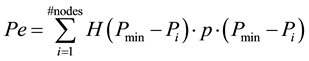 (3)
(3)
The factor p represents a fixed value that becomes effective when 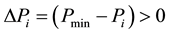 which means that the minimal pressure requirement is not met.
which means that the minimal pressure requirement is not met.
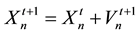
Initially, the process of finding the optimal solution starts from a swarm of particles (we can take a number of particles 1 ® n ® N, N = 100 for example), in which each of them contains a solution needs to be improved by iteration. The n-th particle is associated with a position in an S-dimensional space, where S is the number of variables involved in the problem (the number of pipes in the case of WSS). The values taken by each variable of the S variables (the diameter j of each pipe in the case of WSS) represent a possible solution of the optimization problem. Each particle n is completely determined by three vectors: its current position, in iteration t, 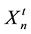 , its best position reached in previous iterations
, its best position reached in previous iterations , and its velocity in the current iteration
, and its velocity in the current iteration :
:
Current position 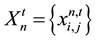 (4)
(4)
which reveals the diameter j of each pipe i, presented by the particle n in the iteration t. So, in every iteration we have N particles and thus N solution.
Best previous position 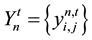 (5)
(5)
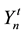 is the best solution presented by particle n before the iteration t.
is the best solution presented by particle n before the iteration t.
Flight velocity 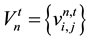 (6)
(6)
The flight velocity depends on the position of the current “solution” comparing to the best solution of all the particles in the same iteration and the best previous solution as explained in Equation (7).
This algorithm simulates a flock of birds which communicate during flight. Each bird examines the search space from its current local position, and this process repeats until the bird possibly reaches the desired position. The birds learn through their own experience (local search) and the experience of their peers (global search).
In every iteration, one identifies the particle which has the best instantaneous solution to the problem; the position of this particle subsequently enters into the computation of the new position for other particles in the flock. This heuristic calculation is carried out according to:
 (7)
(7)
where the primes denote new values for the variables, and the new velocity is given by:
 (8)
(8)
Here, c1 and c2 are two positive constants called learning factors; c1 = 3, c2 = 2, in [5] and they are bound to vary between 0 and 5 in [6] .
 represents a function which creates random numbers between 0 and 1.
represents a function which creates random numbers between 0 and 1.
w is a factor of inertia suggested by Shi and Eberhart [26] , it controls the balance between global and local search; it was suggested to have it decrease linearly with time, usually in a way to first emphasize global search and then, with each cycle of the iteration, to prioritize local search.
![]() (9)
(9)
where t is the iteration number.
Finally, Y* is the best present solution of all Yi.
Once the current position is calculated, the particle directs itself towards a new position.
To control any change in the particle velocities, we introduce the respective upper and lower limits:
![]() (10)
(10)
where Vsup = 50% of the total variable range and Vinf = −Vsup.
This algorithm can be considered as the standard PSO algorithm, which is applicable to continuous systems and cannot be used for discrete problems. In discrete problem, the initial position vectors are generated with integer values, so if the flying velocity vector components are integer values then the new position vectors will be integer values as well. According to this scheme, Equation (7) turns out to be:
![]() (11)
(11)
where ![]() implies that we only take the integer part of the result.
implies that we only take the integer part of the result.
Thus, The PSO algorithm after some modifications can adapt to problems with discrete variables. The approaches which were presented in the works of Montalvo et al. 2008, 2010 [5] [6] have shown satisfactory performance when applied to water supply systems, namely the optimal design of the networks provided by the Hanoi and New York Cities.
However, the choice of the PSO algorithm’s parameters (such as the group’s inertia and acceleration coefficients) seems to be very important for the speed, convergence and efficiency of the algorithm [6] [27] .
4.3. Ant Colony Algorithm (ACOA)
Ant colony optimization algorithms are inspired by the fact that ants are able to find the shortest route between their nest and a food source. Ants deposit pheromone trails whenever they travel. The path taken by individual ants from the nest in search for a food source is essentially random [9] . As more ants travel on paths with higher pheromone intensities, the pheromone on these paths builds up further, making it more likely to be chosen by other ants and thus the shortest path between the nest and a food source is chosen. The main purpose of artificial ant systems is to find solutions to combinatorial optimization problems; mapped on a graph; they also incorporate features that are not found in their natural counterparts [13] .
In order to apply ACOAs to WSS optimization problems, the combinatorial optimization problem under consideration has to be able to be mapped onto a graph![]() , where D is a set of points at which decisions have to be made, L is the set of options j available at each decision point i, and C is the set of costs associated with options L. A set of finite constraints may be assigned over the elements of D and L. A feasible path over G is called a solution X and a minimum cost path is an optimal solution
, where D is a set of points at which decisions have to be made, L is the set of options j available at each decision point i, and C is the set of costs associated with options L. A set of finite constraints may be assigned over the elements of D and L. A feasible path over G is called a solution X and a minimum cost path is an optimal solution![]() . The cost of a solution is denoted by
. The cost of a solution is denoted by ![]() and the cost of the optimal solution by
and the cost of the optimal solution by ![]() as Equation (1) indicates [28] .
as Equation (1) indicates [28] .
Once the problem has been defined in the terms set out above, the ACOA can be applied. The main steps in the algorithm are as following:
1) Trial solutions are constructed incrementally as artificial ants move from one decision point to the next until all decision points have been covered.
2) The cost of the trial solution generated is calculated. The generation of a complete trial solution and calculation of the corresponding cost is referred to as a cycle n. Every ant draws one cycle in iteration, this is why we keep the same abbreviations, n for particle’s number, and N for total particles number in PSO and in ACOA.
3) Pheromone is updated after the completion of one iteration t, which consists of N cycles “N is the number of ants used”. In other words, the construction of N trial solutions means that we have N ants that made N tours or cycles, each one of them presents a solution.
![]() (12)
(12)
where ![]() is the probability that option
is the probability that option ![]() is chosen by ant n in iteration t;
is chosen by ant n in iteration t; ![]() is the concentration of pheromone associated with option
is the concentration of pheromone associated with option ![]() at iteration t;
at iteration t; ![]() is a heuristic factor favoring options that have smaller “local” costs; α and β are exponent parameters that control the relative importance of pheromone and the local heuristic factor, respectively.
is a heuristic factor favoring options that have smaller “local” costs; α and β are exponent parameters that control the relative importance of pheromone and the local heuristic factor, respectively.
When one iteration is completed, then N trial solutions have been constructed, the pheromone trails are updated in a way that reinforces good solutions. The general form of the pheromone update equation is as following [28] :
![]() (13)
(13)
where ![]() is the concentration of pheromone associated with option
is the concentration of pheromone associated with option ![]() at iteration t + 1;
at iteration t + 1; ![]() is the concentration of pheromone associated with option
is the concentration of pheromone associated with option ![]() at iteration t; ρ is a coefficient representing pheromone persistence; and
at iteration t; ρ is a coefficient representing pheromone persistence; and ![]() is the change in pheromone concentration associated with option
is the change in pheromone concentration associated with option ![]() as a function of the trial solutions found at iteration t. The pheromone persistence coefficient has to be less than one and simulates pheromone evaporation. This enables greater exploration of the search space and avoids premature convergence to suboptimal solutions. The pheromone evaporation process is analogue to the mutation process in GA, with the difference that the first is deterministic, whereas mutation in GAs is stochastic.
as a function of the trial solutions found at iteration t. The pheromone persistence coefficient has to be less than one and simulates pheromone evaporation. This enables greater exploration of the search space and avoids premature convergence to suboptimal solutions. The pheromone evaporation process is analogue to the mutation process in GA, with the difference that the first is deterministic, whereas mutation in GAs is stochastic.
![]() is given by Stützle and Hoos 2000 [29] :
is given by Stützle and Hoos 2000 [29] :
![]() (14)
(14)
where n* is the cycle number that results in the best solution during iteration t.
![]() (15)
(15)
where R is pheromone reward factor; ![]() is the cost of the trial solution generated at cycle n, Ppher is pheromone penalty factor and ΔHmax is maximum pressure deficit in the WSS, which is obtained using a hydraulic simulator for each trial solution. Equation (14) clarifies that the amount of pheromone added to each of the options chosen during a cycle is a function of the cost of the trial solution obtained; the better the trial solution, and hence the lower the cost, the larger the amount of pheromone added, and thus the more likely the concerned solution options will be chosen by other ants in next iterations [29] . The steps of generating trial solutions, calculating the costs of the chosen solutions and updating the pheromone concentrations are repeated until certain stopping criteria are met, usually a specified number of iterations.
is the cost of the trial solution generated at cycle n, Ppher is pheromone penalty factor and ΔHmax is maximum pressure deficit in the WSS, which is obtained using a hydraulic simulator for each trial solution. Equation (14) clarifies that the amount of pheromone added to each of the options chosen during a cycle is a function of the cost of the trial solution obtained; the better the trial solution, and hence the lower the cost, the larger the amount of pheromone added, and thus the more likely the concerned solution options will be chosen by other ants in next iterations [29] . The steps of generating trial solutions, calculating the costs of the chosen solutions and updating the pheromone concentrations are repeated until certain stopping criteria are met, usually a specified number of iterations.
4.4. Harmony Search (HS)
The harmony search algorithm was conceptualized from the musical process of searching for a “perfect state” of harmony, such as jazz improvisation, just as the optimization algorithm seeks a best state (global optimum) determined by evaluating the objective function. The harmony quality is enhanced practice after practice, just as the solution quality is enhanced iteration by iteration [12] .
As in other optimization processes in the water network design, the objective function is the pipe cost function; the pipe diameter is the decision variable; the number of decision variables is the number of pipes in the network; the set of decision variable values is the range of possible candidate diameters.
The steps in the procedure of harmony search are as follows [30] :
Step 1. Initialize the problem and algorithm parameters. The HS algorithm parameters are also specified in this step. These are the harmony memory size (HMS), or the number of solution vectors in the harmony memory which is equivalent to the number of particles N in previous algorithms; harmony memory considering rate (HMCR); pitch adjusting rate (PAR); and the number of improvisations (NI), or stopping criterion. The harmony memory (HM), is a memory location where all the solution vectors (sets of decision variables) and corresponding objective function values are stored. The function values are used to evaluate the quality of solution vectors. This HM is similar to the genetic pool in the GA. In the study of Geem 2006 [12] , an HMS of 30 - 100, an HMCR of 0.7 - 0.95, and a PAR of 0.05 - 0.7 were used based on the frequently used value ranges in other HS applications [30] -[32] .
Step 2. Initialize the harmony memory.
![]() (16)
(16)
In Step 2, the HM matrix is filled with randomly generated solution vectors. Each solution undergoes a hydraulic analysis to verify that it satisfies the minimum pressure requirements at each node. As in other Evolutionary algorithms, the penalty in the objective function will cause that the infeasible solutions that violate the minimum requirements, become uneconomic but still have a chance to be included in the HM in the hope of forcing the search towards the feasible solution area.
Step 3. Improvise a new harmony. A new harmony vector, ![]() is generated based on three rules: 1) memory consideration, 2) pitch adjustment, and 3) random selection. Generating a new harmony is called “improvisation”. The HMCR, which varies between 0 and 1, is the rate of choosing one value from the historical values stored in the HM, while (1 ? HMCR) is the rate of randomly selecting one value from the possible range of values (see Figure 2). The value of HMCR is taken generally between 0.8 and 0.95 for diver optimization problems, according to the survey made by Geem et al. 2006 [12] during their research.
is generated based on three rules: 1) memory consideration, 2) pitch adjustment, and 3) random selection. Generating a new harmony is called “improvisation”. The HMCR, which varies between 0 and 1, is the rate of choosing one value from the historical values stored in the HM, while (1 ? HMCR) is the rate of randomly selecting one value from the possible range of values (see Figure 2). The value of HMCR is taken generally between 0.8 and 0.95 for diver optimization problems, according to the survey made by Geem et al. 2006 [12] during their research.
Every component obtained by the memory consideration is then examined to determine whether it should be pitch-adjusted. This operation uses the PAR parameter. If the pitch adjustment decision for ![]() is Yes, is replaced with neighboring value, i.e. the next greater or next smaller diameter with equal chances. The PAR value between 0 and 1, varies considerably from problem to another. Geem 2006 [12] tried the HS optimization on five WSS and the PAR varies in each case from 0.05 to 0.7.
is Yes, is replaced with neighboring value, i.e. the next greater or next smaller diameter with equal chances. The PAR value between 0 and 1, varies considerably from problem to another. Geem 2006 [12] tried the HS optimization on five WSS and the PAR varies in each case from 0.05 to 0.7.
In this step, the application of HM consideration, pitch adjustment, or random selection to each variable of the new harmony vector in turn, help the algorithm find globally and locally improved solutions, respectively.
Step 4. Update the harmony memory. If the new harmony vector ![]() is better than the worst
is better than the worst
![]()
Figure 2. Harmony Search procedure for water supply system design as an example of combinatorial discrete optimization. Adapted from Geem et al. 2006. HMCR: Harmony Memory Consideration Rate, PAR: Patch Adjustment Rate, NI: Number of Improvisations.
harmony vector in the HM, judged in terms of the objective function value, and no identical harmony vector is stored in the HM, the new harmony is included in the HM and the existing worst harmony is excluded from the HM. For the water network optimization problem, the new solution vector also undergoes a hydraulic analysis, just the same as in Step 2.
Step 5. Steps 3 and 4 are repeated until the number of improvisations (NI) is reached.
However, other techniques have also been investigated in this context, such as: Tabu Search (TS), Simulated Annealing (SA) and Shuffled Complex Evolution (SCE).
5. Discussion on the New York City Tunnels Optimization
Given an existing network like the New-York City network shown in Figure 3, the objective is to “renovate” it by considering the increase of the water demand due to the population growth. If the existing network is no longer adequate for the increased demand, that can be translated in pressure violations at several junctions. Thus, the network must be modified by duplicating some of the pipes, i.e., putting new pipes in parallel with the existing ones, at a minimum cost. The decisions one has to take are: 1) Select the pipes that need to be duplicated; 2)
For each of these pipes, choose a diameter within the available diameter set [14] .
Because of age and increased demands, the existing gravity flow tunnels in New-York City have been found to be inadequate to meet the pressure requirements in some nodes (nodes 16, 17, 18, 19 and 20 shown in Figure 3) for the projected consumption level. There are 21 pipelines that may be duplicated with one of the 15 available commercial diameter pipes or zero-diameter pipe, that is, “do nothing”. The total solution space is 1621 = 1.93 × 1025 possible network designs.
In order to solve this optimization problem in real-coding GA algorithm, a real string made of 21 substrings (genes) is used for coding the 21 decision variables “21 pipes that can take one of the 16 discrete diameters”. The fitness of the chromosome that consists of 21 genes is computed through the objective or evaluation function which determines the cost of a solution by summing the cost of the pipes making up the network. Simulation of the network flows and pressure heads is then carried out through EPANET computer program to assess the feasibility of solutions [33] .
Many optimization works were done in the literature for the case of New York City Tunnels optimization. Basing on the literature review made by Coelho and Andrade-Campos [7] in 2014, there are 26 published research works on this exact title, began from the work of Schaake et al., 1969 [10] . For obvious reasons, we choose to compare our Real GA results with recent researches applying equivalent evolutionary algorithms from 2003 and go on. The parameters chosen to run real GA to find the optimal design of New-York WSS in addition to the parameters used by the three other presented evolutionary algorithms to run the same case, as stated in their original references, are illustrated in Table 1.
Table 2 shows the details of four global optimal designs found by the different evolutionary algorithms. All the proposed designs indicate that pipes 16, 17, 18, 19 and 21 require duplication, with the addition of pipe 15 in our viewpoint. The Four presented designs are all feasible hydraulically, i.e. the pressure in the critical nodes is equal or slightly greater than the minimum required pressure as Table 3 shows. It worth’s to be mentioned that
![]()
Table 1. Adjusting different evolutionary algorithms to be used in the New-York tunnels optimization.
GA: Genetic Algorithms,
PSO
: Particle Swarm Optimization,
ACOA
: Ant Colony Algorithm, HS: Harmony Search.
![]()
Table 2. The detailed four designs of New-York City WSS network proposed by EAs.
![]()
Table 3. Total head at critical nodes for New-York City WSS in the EAs’ four proposed designs.
there are other evolutionary algorithms, in the available literature, that have proposed the same cost as Design I (38.64 M$): PSO [5] and NSGA-II “Non-Dominated Sorting Genetic Algorithm” [3] . However, they did not indicate the design details in their published works such as the proposed pipes diameters, the feasibility of their solutions, nor the number of evaluations to reach this cost; this is why we could not place them for comparison in Table 2 and Table 3.
Regarding the four designs proposed by the evolutionary algorithms, the real GA affords two feasible designs “the first after 45,904 evaluations and the second after 116,805 evaluations” with costs comparable to the costs of designs I and II. The availability of alternatives with nearly equivalent costs has a big advantage in practice, because that enables the engineers to take into account other terrain factors to clearly make a choice on the adopted design.
Comparing the performance of the three algorithms in Table 2, we find that the Harmony search presents the least cost with the minimum number of evaluations compared to ACOA and real GA. However, associating these results with the theoretical basics of each algorithm, and with the corresponding parameters in Table 1, reveals that the ACOA needs five parameters to be calibrated, compared with four parameters in GA, two parameters in HS. So, the success of ACOA in obtaining feasible solution with reasonable cost, can be referred to the adopted values of parameters, even if the ACOA handled unrealistically the zero pipe option by assigning a “virtual” unit cost of $70/m for the purpose of calculating the heuristic factor ![]() which is the inverse of the pipe cost used in Equation (11) [13] . The main drawback of GA is that it needs greater number of evaluations than other proposed evolutionary algorithms to reach equivalent solutions. Objectively, we can say that the search process in the harmony search, illustrated in Figure 2, enables the algorithm to discover the research space more efficiently, where it generates solutions randomly, choose neighbor solutions and keep current solutions; while in the Genetic Algorithms, the evolution of a solution depends only on the mutation and crossover process applied on its two parents only. The mutation is a limited operator that considers changing some gens in the solution, so the offspring in GA are more influenced by the initial population than the offspring in other evolutionary algorithms, this is the reason why GA takes longer time to discover the research space and reach the optimal solutions. The process that we propose to improve the performance of real-coding GA, and GAs in general, is to incorporate in every generation, some completely new solutions “chromosomes” that are generated randomly. This process is analogue to the “immigration” process in real life, where these new individuals “solutions” give a new blood to the population, and they are evaluated like other solutions, and couple with existing solutions to find new ones.
which is the inverse of the pipe cost used in Equation (11) [13] . The main drawback of GA is that it needs greater number of evaluations than other proposed evolutionary algorithms to reach equivalent solutions. Objectively, we can say that the search process in the harmony search, illustrated in Figure 2, enables the algorithm to discover the research space more efficiently, where it generates solutions randomly, choose neighbor solutions and keep current solutions; while in the Genetic Algorithms, the evolution of a solution depends only on the mutation and crossover process applied on its two parents only. The mutation is a limited operator that considers changing some gens in the solution, so the offspring in GA are more influenced by the initial population than the offspring in other evolutionary algorithms, this is the reason why GA takes longer time to discover the research space and reach the optimal solutions. The process that we propose to improve the performance of real-coding GA, and GAs in general, is to incorporate in every generation, some completely new solutions “chromosomes” that are generated randomly. This process is analogue to the “immigration” process in real life, where these new individuals “solutions” give a new blood to the population, and they are evaluated like other solutions, and couple with existing solutions to find new ones.
6. Summary
Evolutionary algorithms (EAs) have shown considerable success in solving global optimization of discrete problems and have proved to be a valuable tool in the search for alternatives, and not only a unique solution.
The real-coding Genetic Algorithm GA is based on the phenomena of natural selection, the possible solutions are seen as individuals “chromosome” and they are evaluated basing on their fit to the objective function. The conventional GA uses two main operators applied on the initially generated population and the next generations (mutation and crossover). The real GA approach has considerable flexibility in application to nonlinear problems and to complex systems. In addition, a real GA will generate several near-optimal solutions.
The second presented evolutionary algorithm is the Particle Swarm Algorithm (PSO). Within the PSO algorithm, every solution is a bird of the flock “a particle”. Birds develop some social behavior and coordinate their movement towards a destination which is the objective function. The flight velocity depends on two terms with random portions: the position of the current “solution” comparing to the best solution of all the particles in the same iteration, and the best previous solution.
The third presented evolutionary algorithm is the Ant Colony Algorithm (ACOA).This algorithm is inspired by the fact that ants are able to find the shortest route between their nest and a food source. The ants have tendency to choose paths where other ants have crossed. They can recognize these paths by pheromone intensities deposed by the traveling ants. In the ACOA, the pheromone concentration is an auxiliary parameter used to help artificial ants to make their options.
The fourth presented evolutionary algorithm is Harmony Search (HS). (HS) conceptualized from the musical process of searching for a “perfect state” of harmony, such as jazz improvisation. The harmony memory (HM), is first filled by solution vectors. Improvise a new harmony is generated based on three rules: 1) memory consideration, 2) pitch adjustment, and 3) random selection.
A considerable amount of work is done in this paper for unifying the symbols and notations in the mathematical description of the four mentioned EAs in order to be comparable and easy to understand.
The New-York City WSS tunnels network for WSS, is taken as an example to compare the real GA with PSO, ACOA and HS. The results of the three last EAs are stated in literature. Primarily, the comparison while preparing each algorithm to be applied to a specific case study, reveals that the ACOA needs the biggest number of parameters to be calibrated (5 parameters), compared with 4 parameters in GA, 2 parameters in PSO and HS. Four distinguished designs are offered by the EAs. However, the detailed results of PSO are not included in the published work of Montalvo et al. 2008 [5] , they mentioned only the cost of their solution of 38.64 M$. The same cost is found using ACOA [13] . Our real GA offer two near-optimal designs, the first with a cost of 38.8 M$ after 45,904 evaluations, while the second with a cost of 38.5 M$ after 116,805 evaluations. Harmony search found the least-cost design of 36.66 M$ in the minimum number of evaluations (6000 evaluations).
The superiority of Harmony search in results and performance is probably due to the competent search process illustrated in Figure 2, which enables the algorithm to discover the research space more efficiently, as it generates solutions randomly, choose neighbor solutions and keep current solutions. On the other hand, the Genetic Algorithms takes greater number of evaluations to reach equivalent solutions. The reason of the reduced efficiency of GA compared with HS or ACOA, can be explained as follows: the evolution of solution in GA, depends only on the mutation and crossover process applied on its two parents only. The mutation is a limited operator that considers changing some gens in the solution, so the offspring in GA are more influenced by the initial population than the offspring in other evolutionary algorithms, this is the reason why GA takes longer time to discover the research space and reach the optimal solutions. The process that we propose to improve the performance of real GA, and GAs in general is to incorporate in every generation, some completely new solutions “chromosomes” that are generated randomly. This process is analogue to the “immigration” process in real life, where these new individuals “solutions” give a new blood to the population, and they are evaluated like other solutions, and couple with existing solutions to find new ones.
Finally, we conclude that the four proposed EAs were able to find four near-optimal designs for the same discrete optimization problem with close costs. The existence of these alternatives is a major advantage in practice, where other factors can be taken into account. The time needed by each EAs to reach the optimal or near-op- timal global solutions varies considerably depending on its mathematical construction and the choice of parameters involving. The development of EAs nowadays is moving towards improving their performance and calculation time, since their robustness has been proven.