1. Introduction
Investigation into the mechanism of energy dissipation in heavy-ion reactions has been carried out by different authors from different approaches, an example is the quantum dynamical model of Diaz-Torres, Hinde, Dasgupta, Milburn and Tostevin, which is based on the dissipative dynamics of open quantum systems in this model both deep-inelastic process and quantum tunneling were treated with a quantum mechanical coupled-channels approach [1] and [2] . For some review papers and other approaches to heavy-ion collisions studies, see the following refs. [3] -[11] .
Mshelia, Scheid and Greiner formulated a nuclear energy dissipation theory to account for energy dissipation that occurs in heavy-ion collisions [12] . This was described quantum mechanically as resulting from the coupling of collective degrees of freedom to intrinsic excitations. The formalism has been tested on several analytically solvable models of oscillators coupled to free motion in one-dimension [13] [14] . Recently, Ibeh and Mshelia presented a realistic but complex model for investigating the energy dissipation in physical systems [15] , which was an extension of the one-dimensional models of previous work [13] [14] . The results obtained showed a marked improvement to the previous models comparative to the exact results.
In this paper, we consider some of the salient features in the complex model of Ibeh and Mshelia which consists of three-dimensional coupled oscillators located at the corners of a tetrahedron, three oscillators at the corner of the triangular base representing intrinsic motion while the one at the apex represents the collective motion [15] . In Section 2, we present the derivation of the potential energy and the kinetic energy, leading to the equation of motion of the system. Section 3 deals with the quantization of the Hamiltonian of the dissipative system. In Section 4, the solution of the total and intrinsic Schrödinger equations is presented, while Section 5 consists of the method of determining the probability distribution function.
2. The Classical Hamiltonian
By the symmetry consideration of the arrangement of four particles in space Figure 1 gives the schematic of the vibrating system, consisting of three-dimensional coupled oscillators located at the corners of a tetrahedron- three oscillators at the corners of the triangular base representing intrinsic motion while one at the apex representing collective motion. All oscillators are coupled to each other elastically. Their equilibrium positions are as follows: the particle of mass M is at the point 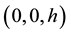 at the apex of the tetrahedron while the other
at the apex of the tetrahedron while the other
three particles are positioned at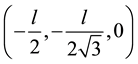 ,
, 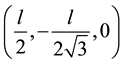 ,
, 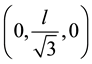 located at the corners of the triangular base.
located at the corners of the triangular base.
For harmonic vibration recall that in classical mechanics [16] -[19] , it is shown that near the equilibrium position the potential energy of the system may be developed in a Taylor series i.e.,
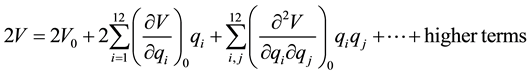 (1)
(1)
in this the only term of interest is the third term, which is sufficient for small amplitude of vibration, so that the harmonic potential energy is approximated to
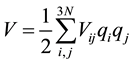 (2)
(2)
in which the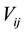 ’s are constants given by
’s are constants given by
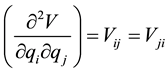 (3)
(3)
The quantities  form a symmetric matrix. Thus the potential energy of the system of Figure 1 about the equilibrium positions of the particles, becomes,
form a symmetric matrix. Thus the potential energy of the system of Figure 1 about the equilibrium positions of the particles, becomes,
 (4)
(4)
![]()
Figure 1. A system of three small mass coupled to each other and each coupled to a large mass.
where the constants, 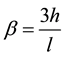 and
and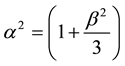 .
.
Similarly the quadratic kinetic energy of the system is
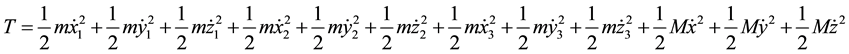 (5)
(5)
where, 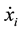 ,
, 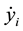 ,
, ![]() and
and![]() ,
, ![]() ,
, ![]() are velocities. i = 1, 2, 3.
are velocities. i = 1, 2, 3.
3. The Quantum Energy Dissipation
In Ibeh and Mshelia [15] the quantized Hamiltonian describing the dissipation of energy from the collective motion into intrinsic degrees of freedom is given as:
![]() (6)
(6)
where the intrinsic and collective Hamiltonians are explicitly stated as:
![]() (7)
(7)
and
![]() (8)
(8)
The collective Hamiltonian is assumed to be that of a free particle with mass, M and described by coordinates![]() . The three oscillators in Figure 1 described by the coordinates
. The three oscillators in Figure 1 described by the coordinates ![]() have the same mass m and are elastically coupled to each other and to the collective motion. Energy can be dissipated from the collective degree of freedom into intrinsic excitations.
have the same mass m and are elastically coupled to each other and to the collective motion. Energy can be dissipated from the collective degree of freedom into intrinsic excitations.
3.1. Normal Modes of Vibration
The total Hamiltonian in Equation (6) is given in terms of Equations (7) and (8) as
![]() (9)
(9)
From the above consideration we observe that the kinetic energy matrix is diagonal while the potential energy matrix is non-diagonal due to the products![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , etc. these off-diagonal terms give rise to the coupling of the collective and intrinsic motions and the coupling of the intrinsic oscillators to each other. By a transformation to normal coordinates the quadratic forms of the kinetic and potential energies in Equation (9), can be reduced simultaneously to sums of squares in these coordinates and their derivatives and hence make the coupled-oscillator problem separable into independent motions, each with a particular normal frequencies [16] -[22] .
, etc. these off-diagonal terms give rise to the coupling of the collective and intrinsic motions and the coupling of the intrinsic oscillators to each other. By a transformation to normal coordinates the quadratic forms of the kinetic and potential energies in Equation (9), can be reduced simultaneously to sums of squares in these coordinates and their derivatives and hence make the coupled-oscillator problem separable into independent motions, each with a particular normal frequencies [16] -[22] .
The normal frequencies are determined by the secular equation
![]() (10)
(10)
where the coefficients ![]() and
and ![]() are the elements of the kinetic and potential energy matrices, respectively.
are the elements of the kinetic and potential energy matrices, respectively.
Using the matrices of the kinetic and potential energies according to Equation (9), we obtain from Equation (10) the following twelve eigenfrequencies:
![]() (11)
(11)
where, the constants appearing in the eigenfrequencies above are defined as follows:
![]()
Note the two double degenerate frequencies namely Ω1 = Ω3 and Ω2 = Ω4 and the two non-degenerate eigenfrequencies Ω5 and Ω6 describing the motion in which all the four particles vibrate about their common equilibrium configuration. The six eigenfrequencies: Ω7; Ω8; Ω9; Ω10; Ω11 and Ω12 which vanish are assumed to consists of the three zero eigenfrequencies Ω7, Ω8, Ω9, corresponding to the eigenmodes describing a uniform translational motion of the system as a whole, while the remaining three zero eigenfrequencies Ω10, Ω11 and Ω12 have no direct bearing on the theory of energy dissipation in this work. The corresponding transformations to normal coordinates are obtained as:
![]() (12)
(12)
In terms of the normal coordinates the quantum mechanical total Hamiltonian is
![]() (13)
(13)
3.2. The Solutions of the Schrödinger Equation for the Total and Intrinsic Hamiltonians
We now obtain solutions of the time-independent Schrödinger equation with the decoupled total Hamiltonian H given by Equation (13).
![]() (14)
(14)
Since H describes a free translational motion of the centre of mass and the decoupled harmonic oscillators in the g1, g2, g3, g4, g5 and g6 degrees of freedom the eigenvalues and eigenfunctions are obtained as,
![]() (15)
(15)
and
![]() (16)
(16)
where, the quantum numbers are![]() . and
. and![]() ,
, ![]() ,
, ![]() are the wave numbers of the plane-wave functions for the centre of mass, normalized by means of the Dirac δ-function [23] [24] are given by
are the wave numbers of the plane-wave functions for the centre of mass, normalized by means of the Dirac δ-function [23] [24] are given by
![]() (17)
(17)
The normalized, bound state, wave functions of the harmonic oscillators are written as
![]() (18)
(18)
The quantity ![]() is a Hermite polynomial of order
is a Hermite polynomial of order ![]() and the
and the ![]() s are the inverse oscillator lengths given by
s are the inverse oscillator lengths given by
![]() , (19)
, (19)
the normalization constant ![]() occurring in Equation (19) is defined by
occurring in Equation (19) is defined by
![]() . (20)
. (20)
The total wave function in Equation (16) is normalized as follows:
![]() (21)
(21)
The intrinsic Hamiltonian can be stated in terms of intrinsic coordinates defined as following
![]() (22)
(22)
The resulting eigenvalue equation of the intrinsic Hamiltonian is
![]() (23)
(23)
where ![]() are the intrinsic normal coordinates defined in terms of the intrinsic coordinates given in Equation (22).
are the intrinsic normal coordinates defined in terms of the intrinsic coordinates given in Equation (22).
Solving Equation (23) results in the eigenvalues
![]() (24)
(24)
And the following set of eigenfrequencies and eigenfunctions:
![]() (25)
(25)
where, the constants appearing in the eigenfrequencies above are defined as follows:
![]()
the normalized intrinsic oscillator eigenfunctions:
![]() , (26)
, (26)
where, the intrinsic inverse oscillator lengths and normalization constants are respectively,
![]() , (27)
, (27)
![]() (28)
(28)
From Equation (26) the total intrinsic wave-function becomes
![]() (29)
(29)
4. The Probability Density Functions
The fact that the intrinsic Hamiltonian eigenfunctions obtained form a complete set, by use of the completeness relation the total wave function ![]() is expanded in terms of the complete or-
is expanded in terms of the complete or-
thonormal set of oscillator functions![]() . The normalization of
. The normalization of ![]() gives
gives
![]() (30)
(30)
since the![]() ’s are orthonormal. The expansion coefficients
’s are orthonormal. The expansion coefficients ![]() represent the probability amplitude for excitation of the intrinsic motion [25] .
represent the probability amplitude for excitation of the intrinsic motion [25] .
On the other hand, the normalization of ![]() with respect to the variables g1, g2, g3, g4, g5 and g6 gives
with respect to the variables g1, g2, g3, g4, g5 and g6 gives
![]() (31)
(31)
The relationship between the left hand and the right hand of Equations (30) and (31) is given by the transformation
![]() (32)
(32)
When values are substituted the Jacobian is
![]() (33)
(33)
Comparing Equations (31), (32) and (33) the normalization condition
![]() (34)
(34)
Equation (34) gives a measure for the probability for intrinsic excitation from collective motion [15] . It should be noted that the derivation of Equation (34) demonstrates that the form of the collective amplitude, ![]() satisfy the normalization condition for the total wave function.
satisfy the normalization condition for the total wave function.
The collective amplitude is the expansion coefficient of the total wave function ![]() when expanded in terms of the complete orthonormal set of oscillator functions
when expanded in terms of the complete orthonormal set of oscillator functions![]() , and its form can be obtained by using Equations (12), (16), (17), (18) and (22), which then leads to the probability distribution
, and its form can be obtained by using Equations (12), (16), (17), (18) and (22), which then leads to the probability distribution ![]() as functions of interesting physical parameters for example, energy, intrinsic and collective quantum numbers, etc.
as functions of interesting physical parameters for example, energy, intrinsic and collective quantum numbers, etc.
5. Conclusions
This work has shown that the harmonic approximation of the Hamiltonian of coupled oscillators leads to a Schrödinger equation which describes the coupling of collective degree of freedom, represented by free motion with intrinsic degrees of freedom, represented by three coupled oscillators. This model explains the mechanism for energy dissipation in a physical system, based on the coupling of intrinsic and collective degrees of freedom. The model can be extended to nuclear fission and heavy-ion reactions, where the collective degree of freedom is the relative coordinates of the two heavy-ions and the intrinsic degrees of freedom are the single-particle degrees of freedom [22] .
Furthermore, of current interest and one which is an extension of the above model is the cluster model consisting of a dinuclear system which is not easily solvable analytically because it includes other degrees of freedoms such as butterfly, belly-dancer-type motions, γ-and β-vibrations, etc., of individual nuclei, this model is based on the assumption that cluster-type shapes are produced in the mass asymmetry of nuclear molecules. Theoretical and experimental evidences exist that show that this model is capable of explaining many of the features of deformed heavy nuclei [26] - [38] . An example of such features is the resent work of Adamian, Antonenko and Lenske, in which the linear response theory was used to calculate the mass parameters for collective variables of the dinuclear systems formed in cold fusion reactions and found that the microscopic mass parameter in the neck is larger than the one obtained using the hydrodynamical model [39] .
NOTES
*Corresponding author.