A Note Regarding Prioritization on Congestible Networks

Samuel Raisanen

Department of Economic, Central Michigan University, Mount Pleasant, MI, USA.

DOI: 10.4236/tel.[phone]                

Abstract

This paper examines the effect of allowing prioritization of traffic on a congestible network under three demand scenarios. First, it is shown that when prioritization does not affect usage, average congestion on the network increases. Second, this result is shown to hold when there is demand shifting toward the prioritized network service but no impact on total network traffic. Finally, it is proven that for prioritization to reduce average congestion on a network it must reduce the total traffic on the network.

Keywords

Congestible Networks, Net Neutrality, Regulation

1. Introduction

On February 26, 2015, the US Federal Communications Commission (FCC) revised their Open Internet rules. These rules outline three main sets of regulations. First, Internet service providers (ISPs) cannot block access to legal content. Second, they cannot throttle access on the basis of content. Finally, and subject to much debate, the FCC disallows paid prioritization. Paid prioritization would allow ISPs to divert capacity to some content over non-prioritized content in exchange for compensation from the content provider.

A number of recent papers debate that network neutrality and paid prioritization would have an effect on consumer welfare and capacity investment. Some argue that allowing service providers to monetize capacity though paid prioritization will cause them to invest in additional capacity and use their capacity more efficiently. Proponents of allowing paid prioritization include Chen and Nalebu [1] , Hermalin and Katz [2] , Krämer and Wiewiorra [3] , Sidak and Teece [4] , and Singer and Litan [5] . Others argue that paid prioritization would alter the incentives for the service provides such that they could increase profits by slowing non-prioritized traffic rather than increasing speeds for prioritized traffic. This would create a “fast” and “slow” lane for traffic. Cheng et al. [6] , Economides and Tåg [7] , Chettiar and Holladay [8] and Pil Choi and Kim [9] espouse variations of this view.

In this note, I examine how network congestion would be affected by prioritized traffic for a given level of capacity. Three cases are compared. First, it is shown that when consumer usage of all network services is perfectly inelastic, prioritization of some traffic increases average network congestion. Second, this result is expanded to the case where total network traffic is inelastic but traffic shifts toward the prioritized service. Finally, it is proven that for prioritization to reduce average congestion on a network it must reduce the total traffic on the network. In other words, less congestion for the prioritized traffic is insufficient to reduce average congestion unless the corresponding increase in congestion on the non-prioritized traffic reduces demand for the network overall.

2. Prioritization and Network Congestion

To model network congestion, I expand upon the seminal MacKie-Mason and Varian [10] framework of a congestible network by allowing for multiple services to run on a single network. Content providers supply excludable services on the network while the access provider runs the network itself. Additionally there may be a number of non-excludable, default network services available. Let the set of services offered be indexed where 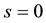are the non-excludable services and 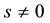are the excludable services. Index consumers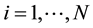, then 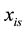denotes person-i’s usage of service-s on the network. Person-i has network

consumption vector Demand for the network by person-i is, total use of service-s is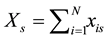, and total use for the network is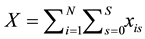. Each user gains utility from the consumption of each service but is negatively impacted by congestion on the network. For a network with bandwidth capacity K, the level of congestion can be defined as.

To include prioritization into the model, let there be one content provider, 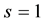, who can pay the access provider a fee F for a guaranteed congestion factor of, where 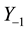is the congestion of all other traffic. Denoting the capacity dedicated to the prioritized content provider as 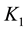it holds that

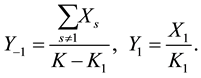
Thus, to maintain congestion 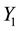for prioritized traffic, a network with capacity must allocate more of that capacity to the prioritized usage as traffic to that use increases. In other words, is endogenous. Solving for and substituting into the equation for yields

(1)

From this equation come two key observations. First, the capacity is separable and constant-sum. Solving (1) for shows

Unsurprisingly, capacity diverted to the prioritized traffic as increase must be lost, one-for-one, from the rest of the network. Second, congestion for users on the non-prioritized portion of the network increases more for an additional unit of traffic by prioritized users than for an additional unit of traffic by non-prioritized users.

The effect of increasing traffic for a non-prioritized service, , is The effect of increasing prioritized traffic on congestion for non-prioritized traffic is. As long as the prioritized traffic is guaranteed lower congestion than the non-prioritized traffic, prioritized traffic causes more congestion for non-prioritized traffic than does other non-prioritized traffic, As a direct consequence, prioritization leads to an increase in the average congestion that a unit of traffic faces.

Theorem 1. Given average congestion without prioritization usage of services for

, capacity, and prioritized traffic congestion of, then average congestion with prioritized traffic is larger than average congestion without prioritization:

This result presumes that demand for each of the services is perfectly inelastic. It is unrealistic to assume that as service is guaranteed lower congestion that it will not receive increased traffic. People will switch from other services to use the more of the prioritized service. As traffic flows to the prioritized service the prioritized traffic faces lower congestion and the non-priority traffic faces higher congestion. As demand for the prioritized service increases, the prioritized traffic will require more of the total capacity in order to maintain a constant level of congestion. This reduces the capacity available for the non-prioritized traffic increasing its congestion. Because the level of congestion guaranteed to the prioritized traffic is lower than the level of congestion of the non-prioritized traffic, the required capacity diversion is such that the average traffic faces increased average congestion.

Now, to simplify the notation, let a negative index on demand denote demand for all services except the magnitude of the index, e.g..

Theorem 2. For a given level of capacity, total demand, and prioritized congestion,

for all where, , , , and Additionally, the result only holds with equality when or.

While Theorem 2 states that when total demand is inelastic, prioritizing traffic increases the average level of congestion, the proof does not require that the guaranteed level of congestion for prioritized traffic be less than before prioritization (see Appendix). In fact even deprioritized traffic will increase the average level of congestion as long as it does not eliminate usage of the deprioritized service. As such, Theorem 2 states that to minimize the average congestion traffic on a network faces, Net Neutrality is the required policy.

When total demand for the congestible resource is not perfectly inelastic with regard to prioritized traffic, demand can either increase or decrease as prioritized congestion is reduced. Total demand may increase if prioritization of a given service attracts new users to the network. On the other hand, total demand may be reduced by prioritization if the corresponding increase in congestion for non-prioritized traffic sufficiently discourages network usage. Theorem 3 states that average congestion can be reduced only in the case where prioritization of some traffic causes total demand for the network to decline.

Theorem 3. Defining the average network congestion as and the absence of prioritization as then

if and only if

Figure 1. Prioritized traffic and average congestion.

Figure 1 summarizes these results by showing how guaranteeing lower congestion for prioritized traffic affects the average level of congestion faced by traffic on the network. When demand for all services is constant with respect to congestion, average congestion increases slowly as some traffic is prioritized. If total network usage is constant but traffic shifts towards the prioritized services then average congestion increases quickly as some traffic is prioritized. When prioritizing some traffic leads to a net decline in network traffic, prioritization initially decreases the average congestion on the network. This effect, however, is limited and guaranteeing lower and lower congestion for the prioritized service will eventually increase the average level of congestion on the network.¹

3. Concluding Remarks

While this paper is agnostic on the efficiency of paid prioritization and network neutrality, it is strongly suggestive that any prioritization scheme will lead to higher network congestion. When the cost of changing network capacity is large, firms will alter their capacity infrequently. As such, capacity can be taken as a sunk investment and congestion will depend primarily on usage. As firms are unlikely to use prioritization to reduce demand for their network, the above results can be taken to show that in the absence of a net neutrality rule average congestion on the network will increase.

Acknowledgments

I would like to thank the participants at the 2015 Western Economic Association International session 27 for their invaluable suggestions.

Proof Appendix

Proof of Theorem 1

We want to show that combining all traffic to use capacity results in a lower average congestion than prioritizing traffic ensuring traffic receives congestion and the remaining traffic has congestion deter-

mined by the remaining capacity. Formally stated this says, given, and such that, then

Proof. For temporary simplification of notation, let and Given that for all and we are assured that, ,. Additionally,. We proceed by algebraic manipulation from

Since and are strictly positive,

and because

Algebraic manipulation verifies that thus

As we continue multiplying by.

Substituting for and gives

Rearranging the definitions of and to solve for capacity yields and. Substituting in for capacities and and then substituting for yields our result.

Proof of Theorem 2

Proof. Given that then for all and,

Additionally, this is a strict inequality whenever and. Expanding and substituting for yields

Multiplying through by and expanding gives

From here adding terms to each side of the inequality and algebraically rearranging using the appropriate substitutions yields the result.

Proof of Theorem 3

Proof. Each of the following implications is bidirectional and follows from and the definitions of and.

Given that if follows

Dividing by and algebraically rearranging yields

NOTES

¹For readability, the case of increased demand for the network due to prioritization is omitted from the graph. This relationship is bounded below by the total usage inelastic curve.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Chen, M.K. and Nalebu, B.J. (2006) One-Way Essential Complements. Cowels Foundation Discussion Paper.
[2]	Hermalin, B.E. and Katz, M.L. (2007) The Economics of Product-Line Restrictions with an Application to the Network Neutrality Debate. Information Economics and Policy, 19, 215-248. http://dx.doi.org/10.1016/j.infoecopol.2007.04.001
[3]	Kramer, J. and Wiewiorra, L. (2012) Network Neutrality and Congestion Sensitive Content Providers: Implications for Content Variety, Broadband Investment, and Regulation. Information Systems Research, 23, 1303-1321. http://dx.doi.org/10.1287/isre.1120.0420
[4]	Sidak, J.G. and Teece, D.J. (2010) Innovation Spillovers and the “Dirt Road” Fallacy: The Intellectual Bankruptcy of Banning Optional Transactions for Enhanced Delivery over the Internet. Journal of Competition Law and Economics, 6, 521-594. http://dx.doi.org/10.1093/joclec/nhq003
[5]	Singer, H.J. and Litan, R.E. (2007) Unintended Consequences of Net Neutrality Regulation. Journal on Telecommunications and High Technology Law.
[6]	Cheng, H.K., Bandyopadhyay, S. and Guo, H. (2011) The Debate on Net Neutrality: A Policy Perspective. Information Systems Research, 22, 60-82. http://dx.doi.org/10.1287/isre.1090.0257
[7]	Economides, N. and Tag, J. (2012) Network Neutrality on the Internet: A Two-Sided Market Analysis. Information Economics and Policy, 24, 91-104. http://dx.doi.org/10.1016/j.infoecopol.2012.01.001
[8]	Chettiar, I.M. and Holladay, J.S. (2010) Free to Invest: The Economic Benefits of Preserving Net Neutrality. Report No. 4, Institute for Policy Integrity, New York University School of Law, New York.
[9]	Pil Choi, J. and Kim, B.-C. (2010) Net Neutrality and Investment Incentives. The RAND Journal of Economics, 41, 446-471. http://dx.doi.org/10.1111/j.1756-2171.2010.00107.x
[10]	MacKie-Mason, J.K. and Varian, H.R. (1995) Pricing Congestible Network Resources. IEEE Journal on Selected Areas in Communications, 13, 1141-1149. http://dx.doi.org/10.1109/49.414634