Formalized Operators with Phase Encoding

Nikolay Raychev^*

School of Computing, Varna University of Management, Varna, Bulgaria.

DOI: 10.4236/jqis.2015.53014                

Abstract

In this article the concept of phase encoding/decoding is used to analyze and formalize a simple quantum algorithm—the Deutsch’s algorithm. The algorithm is formalized in two different ways through an analysis, based on phase encoding/decoding, carried out by the formalized elementary operators developed by the author of this article. Concrete examples of different possible realizations of the formalized with Raychev’s operators Deutsch’s algorithms are offered.

Keywords

Quantum Operators, Rotations, Phasespace, Quantum Circuit

1. Introduction

Quantum computers can be useful in solving many important and complex issues such as solving many fundamental and complex problems such as integer factorization [1] , database search [2] , global binary optimization [3] , linear equation solving [4] , and so on [5] . The reversible computation and reversible universal logic operator was first proposed by Toffoli [6] . Based on the work of Toffoli, Bennett first implement efficient algorithm with reversiblelogic [7] . Based on the work of Toffoli and Bennett, Deutsch defines a three-qubit operator [8] . As a result of the Deutsch’s work, a plurality of other universal operators [9] - [12] were found. On this basis in recent years several other complex surveys have been created [13] - [15] . This report described an approach for encoding and decoding of discrete information about basic states at the input of operators in the phase of their outputs. The decoding is viewed as a special case of interference with four different decoding forms that reflect the identity classes and negation operators. The formalized qubit operator developed by the authors [16] - [24] , which is described in this research, uses the decomposition of the phase/amplitude, which characterizes the operators, presented in the report. The formalized operator permits operation with single qubit operators as linear combinations of the identity operator and the negation operator. In such case, a single qubit operator either negates, identifies, or performs partial identity/negation. If an operator decodes another one, it is able to read the information encoded in the phase space, and reduce the encoded bits to a state or its negation. Relationships of decoding have been developed both as regards to the operator parameters and in terms of Boolean functions encoding. This in addition leads to an increase in the abstraction level. The proposed system approach is different from previous discussions for phase encoding, making the encoding a substantial part of all operators so that the correct encoded information can be determined from the operators parameters.

Both Identity₁ and Negation₁ classes are analogous to the classic operators and therefore the formalization of single qubit operators with these classes, acting as main operators, ensures means for primitive operators operation, set out in the classical concepts for calculations. The main goal is the parts of the state phase to be separated from those of the amplitude in such a way that should be set out as the key models at the interference, generated by the operators. This interference is a key to the quantum calculations and the quantum algorithms development. In addition, the separation permits the strict characterization of the consequences from a change of the phase as the binary information encoding in a phase space and thus permits the characterization in terms of Boolean functions. This report will consider the necessary and sufficient conditions for combining operators from Identity₁ and Negation₁ for formation of unitary operators and provision of an abstraction on the relative weights of the base operators. The logical formalization of the main operators will be addressed as regards to their phases and phase changes, which they carry out, on the states, to which they are applied. Whereas this approach to elementary controlled operators is elementary, the formalized system for designing of quantum circuits algorithmic models offers a second approach, which unites the elementary controlled operations with another important aspect of multitude of quantum algorithms, the Oracle operators. In the quantum algorithms design a standard technique is the use of an Oracle operator to enact a phase-kickback operation. Herein an arbitrary, probably irreversible function 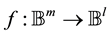is encoded into an n = m + l qubit operator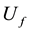, such that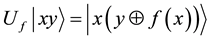, where, and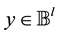. Usually higher degree bits for x and with a lower degree for y shall be used. The same could be performed vice versa where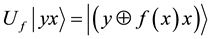. In both cases 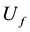acts as an Oracle for f. Such operations are accepted as the controlled application of l qubit operator, where x acts as a control bit, and y as a target bit. The phase kick-back happens when the target qubits are set to an own state, and the value of f(x) is encoded into the resulting state phase. It is possible this conception for the controlled operations to be applied to an elementary, two qubit controlled operators, which will provide a new means for viewing the elementary controlled operations behavior and the interference patterns that they generate. In order to generalize the behavior of a 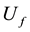-type operator, the option to occur phase shifts in addition to the main changes must be enabled. In 1985 Deutsch offers a probabilistic algorithm [5] , which allows for Oracle function g: In ® B to be calculated 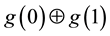with a probability of 1/2, using only 1 application of G: If G: 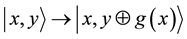is a two qubit oracle operator, realizing the boolean oracle function g: In ® B. The register x will contain the value 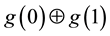each time, when 1 is measured in y, which in turn occurs in 50% of the cases. Although strictly speaking this does not provide an acceleration relative to the classical case, if it is taken into account that on average 2 trials are needed for the actual measurement, then the Deutsch’s algorithm is the first evidence that the quantum computers are capable of computations in ways impossible for the classical computers. As a whole, in order to achieve any acceleration relative to the classical algorithms, it is necessary to be used the unique characteristics of the quantum computations, namely

・ Superposition (step 2)

・ Quantum parallelism (step 3)

・ Interference (step 4)

Deutsch’s algorithm has been explored many times [3] [4] . In this paper we want to focus mainly on the phase encoding and decoding with formalized Raychev’s operators.

The Deutsch’s algorithm points out the basic principles of the quantum algorithms, while requiring a small and relatively easy to understand circuit. Here it will be studied anew through the prism of the phase encoding and decoding and will be given more common characteristic of the algorithm. First, let’s recall the algorithm and its standard presentation. The problem of Deutsch is to determine if a single bit boolean function is in BAL or CONST at given quantum external source of information, black box, to that function. It requires a single query of the source, where a classical approach would require two. Figure 1 gives the standard circuit for Deutsch’s algorithm. The Deutsch’s algorithm is a key element of the introduction to the quantum computations and has been analyzed many times [3] [4] . Specifically this analysis is focused mainly on the phase encoding and decoding relationships in an attempt to generalize the construction of the circuit.

Particular attention will be paid to three elements of the Deutsch’s algorithm, as it is presented in Figure 1.

Figure 1. Algorithm of Deutsch.

1) The Hadamard operator H, which is applied to 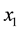at the start and end of the algorithm, is its own identity decoder. Thus the effect of the initial and final can be considered as encoding and decoding of the initial state of.

2) The composition of with an oracle operator forms an degree operator.

3) The selection of an initial state of the working qubit plays a role in the result of the algorithm. The conditions for the initial state of the working qubits can be expressed and explained in respect of the encoding/de- coding results.

2. Formalizations of the Deutsch’s Algorithms

To examine the conclusions from these observations isproposed the three-part decomposition.

The algorithm is divided into three logical steps: the application of, followed by the Oracle operator VC, and finally the application of (Figure 2). The analysis will begin by passing through the algorithm in order to examine the state of the system with respect to the operator parameters.

If, then, where

If and, where and such that

.

Similar formulation of V allows the phase changes to be introduced by the Oracle operator in addition to the conditional basis changes. By Theorem 1 VC is α degree operator. If

and denotes the phase function of when, and vice versa, when.

In this analysis the two operators of O are effectively indexed via the function f. In a similar way, the amplitude parameter of O can be indexed. If denotes, when, and, when.

Then is such that,

(1)

Figure 2. Formalized three-partdecomposition.

The final step of the algorithm generates interference between the operator A and B. If, then. The final state of the circuit, is given in Equation (2). The formulas are rearranged, in such way that the results of the operators, generating the interference, are next to each other.

(2)

If the general formulas for the probability amplitude of each basis state shown in Equation (2) are given, the Deutsch’s algorithm can be generalized in the context of the formalized Raychev’s operators. The general character of the output data will be maintained in such way that the final state should leave unchanged, if f is constant, and change it if f is balanced. The first observation is that the final operator of the Deutsch’s algorithm is a decoder of the initial operator. The decoding connections may be outlined in terms of the phase numbers, as shown in Table 1.

Until now the decoding was limited to the conditions under which the two operators are combined in order to form a certain basis operator. The requirements for the parameters are shown in Table 2.

This is done within the limits of the formalized Raychev’s operators. More common structure of the decoding operators occurs when calling the main matrix formulation of the operators.

When B is a decoder of A, can be found the interference pattern, generated by B, from Table 1. More specifically, if В is a decoder of A, then there exists some such that and. When B is an identity decoder, g characterizes the phase change in the states that identify, i.e. the states left after the decoding operation, and the functions h and k determine the interference generated in the states, where is with a negative value. Furthermore, when В is an identity decoder of A, then the amplitude parameter is equivalent to. From here, when B is an identity decoder of A, Equation (2) can be simplified to Equation (3).

Table 1. The negation decoding by phase number γιη.

Table 2. The decoding operators.

(3)

If an attention is paid to the Oracle operator and how f controls its impact on the development of the system. If f is a constant function, then and Equation (3) can be further simplified, as this means that only one of the two subspace operators, and will be used by the Oracle operator.

(4)

In Equation (4) is seen that the encoding, performed by the Oracle operator, in each term of the sum of the probability amplitudes is the same. Thus, no interference is generated by the Oracle operator and the final state of the circuit is reduces down to the decoding interaction between A and B. The intervention carried out relative

to the states and, obviously leads to zero probability amplitudes when f is constant. Thus leaving

the state in a superposition of and. It is worth noting that achieving the interference necessary to leave unchanged at f constant, is independent from the initial state of the system. Now the impact of the Oracle operator will be considered when f is balanced. As mentioned earlier, the goal is to create a system in which the value of has changed. If f is balanced, both operators and will be used by the Oracle operator. This is implied by the fact that. Under the given and, if is the amplitude of, then the amplitude of must be. This means that and allows us to further simplify Equation (3).

(5)

If the goal is the probability amplitudes of and to become zero when f is balanced, then it is

clear that should be established such that and. This will make the

terms of the probability amplitude sums in and equivalent and will enable the interference to reduce the final probability amplitudes to zero. From Equation (9.5) it is seen that, when

and then the entire necessary interference

will occur; the probability amplitudes of and will be inverse to each other, and all other probability amplitudes will constructively interfere. What was determined is that the desire to have and

destructively interfere sets many of the requirements for correctness of the algorithm. The desired inter-

ference can be guaranteed regardless of the value of, if an Oracle operator O is defined such that

. This construction is not intuitive, as it requires the Oracle operator V

to be defined not as the Oracle typical for the Deutsch’s algorithm, but as an operator in, which carries out a global phase shift that is conditionally upon the function f. The conditional phase shifts are used in the Grover’s algorithm and therefore this particular operator is not something new in the quantum computations [5] .

2.1. Formalized Deutsch’s Algorithm: Version 1

Problem: Upon given Oracle like operator, to be determined whether is constant or balanced.

Preconditions:

1) To be defined В and А such that and the amplitude parameter of A is.

2)

Result: If the function f is balanced, and otherwise, i.e. when f is constant, then (Figure 3).

For Boolean function, where m < n, the generalized controlled operator can be used to represent operators, as well as degree version of these operators. Theorem 1 describes the construction of an operator in the set whereas Theorem 2 shows the construction of an degree version of a operator.

Theorem 1 If operator is such that A Î The set of the identity formalized Raychev’s operators, B Î The set of the negation formalized Raychev’s operators and, where m < n. Then

.

Proof. If it is assumed that A Î The set of the identity formalized Raychev’s operators and B Î The set of the negation formalized Raychev’s operators, therefore for each n qubit basis,

(6)

Theorem 2 If operator is such that and. Then V is an degree.

Proof. If it is assumed that and. Then, for each n qubit basis,

Figure 3. Formalized Deutsch’s algorithm: Version 1.

(7)

Theorem 1 leads to general means for constructing of degree operators from an elementary indexed operator and an operator in.

Theorem 3 If V is an n qubit operator with target bit t and is indexed, formalized operator with

an amplitude parameter, such that. Then the operator VA is degree operator.

Proof. The proof follows from theorems 1 and 2, by noting that when, then .

Theorem 3 is important because, it captures a common occurrence in the quantum algorithms: setting the target bit of an Oracle operator to a superposition and then applying the oracle operator. In the formalized system for designing of algorithmic models for quantum circuits this can be addressed in the context of an α degree operator.

The composition of random formalized operators with main operators can be expressed in terms of the transformations of parameters.

Formal prerequisite 1 If the operator. Then

(8)

Proof. If A is a base operator. Then

If the consideration is limited only to the original formulation of the problem, i.e. Oracle only, then the problem of Deutsch still can be solved deterministically, by choosing an appropriate starting value for, the

target big of and C. The amplitude parameter of C can be set to. By Theorem 3, the oracle operator

is combined with C, to form an Oracle. At the subspace oper-

ators of the composite operator are and. The exact phase of

and is determined through Theorem 4.

Remark The generalization of the Deutsch’s algorithm given in Figure 2, also covers the case when are used classical, i.e. without a phase change, oracle operators of the form as the ones used in the standard version of the Deutsch’s algorithm. Then the precondition for the value of is limited to a condition on the phase of operator C and the initial value of only.

2.2. Formalized Deutsch’s Algorithm: Version 2

Problem: Upon given Oracle operator, should be determined whether is constant or balanced.

Preconditions:

1) To be defined В and А such that and the amplitude parameter of A is.

2)

3) For operators and, should be chosen initial value for such that

and.

Result: If the function f is balanced, and otherwise, i.e. when f is constant, then (Figure 4).

If. Then should be chosen such that and

.

Two generalized algorithms for solving the Deutsch’s problem are developed, by re-examining anew the standard formulation of the Deutsch’s algorithm. In both cases are used the specific phase encoding and decoding ideas, realized by the developed by the author of the report formalized operators. Both algorithms set the initial state to be equal to a superposition of all possible two qubit states and in this way set the working bit to

an own state of the Oracle operator. Furthermore, the use of Hadamard-like gates with amplitude parameters is, in general, a requirement of the algorithm if deterministic results are sought.

Finally, the formalizations of the Deutsch’s algorithm, given in Figure 3 and Figure 4, are reduced to the ability to work in many different phases, possible within the quantum computations. Perhaps the most interesting result of the analysis, based on the phase decoding, is the reaching to formalization of the algorithm in Figure 1 in the style of Grover. This version will lead to results, which would be expected upon solving the Deutsch’s algorithm, independently of its input data, but requires an Oracle operator for phase shifting as opposed to the traditional formulation of the Oracle operator in the Deutsch’s problem. The result is inherited by the explicit characterization of the behavior upon phase encoding / decoding of the operators, based on their formalization.

2.3. Examples of Formalized Algorithm for Solving the Deutsch’s Problem

The first example deals with a slight variation of the traditional Deutsch’s algorithm.

Let operator with identity decoder such that. If defines Oracle operator, where and. When the target qubit, O and

preparation of target qubit are equivalent to traditional Deutsch’s algorithm. From Equation (2) can determine the final state of the system, if the input data are given for the traditional algorithm.

Figure 4. Formalized Deutsch’s algorithm: Version 2.

When f is constant, then the phase encoding executed by Oracle operator is the same in both terms of any amount. Without loss of generality, let us assume that, then. Thus is obtained the following result

When f is balanced then, with encoding function, is applied when, and

, with encoding function is applied when. It should be noted

that for and preconditions are met. Thus, when,

If we consider the example of the algorithm represented in Figure 1. Let operator with identity decoder such that. If it defines such Oracle operator, such that for each operator,. It is seen that for any

input this algorithm will have the same result as Deutsch’s Algorithm.

Without loss of generality, let us assume that for a balanced and

such that they correspond to the phases of C and ?С, respectively Oracle subspace operators. That leaves the following final state.

In the case where f is a constant, there is the same overall result as the standard formulation of the Deutch’s algorithm; the Oracle operator makes no interference between the subspace and the calculation is reduced to the decoding effect B has on A.

3. Conclusions

Figure 1 and Figure 2 present two formalizations of the Deutsch’s algorithms. The first requires Oracle operators, oriented to phase change, while the second formalization effectively establishes, how different operator phases can be used in the context of the standard structure of the Deutsch’s algorithm. The analysis which leads to the Formalizations, strongly leans to the close relationships and properties of the boolean encoding functions of the formalized Raychev’s operators, included in the algorithm.

The first version of formalized algorithm uses phase change operations where the second version demonstrates how different phases might be used in the context of the conventional Deutsch’s algorithm.

The formalized Raychev’s operators separate the parts of phase and amplitude and allow for expression of amplitude in terms of probabilities as opposed to more general probability amplitudes. This formalization is further improved by the characterization of classes with defined relations and incarnation of formalized logic parameter γ on the global phase. Under the needed and sufficient conditions to construct a unitary, in this case orthogonal operators are incorporated into the formalization.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Shor, P. (1997) Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. SIAM Journal on Computing, 26, 1484-1509. http://dx.doi.org/10.1137/S0097539795293172
[2]	Childs, A.M., Landahl, A.J. and Parrilo, P.A. (2007) Quantum Algorithm for Ordered Search Problem via Semidenite Programming. Physical Review A, 75, Article ID: 032335. http://dx.doi.org/10.1103/PhysRevA.75.032335
[3]	Farhi, E., Goldstone, J., Gutmann, S., Lapan, J., Lundgren, A. and Preda, D. (2001) A Quantum Adiabatic Evolution Algorithm Applied to Random Instances of an NP-Complete Problem. Science, 292, 472-475. http://dx.doi.org/10.1126/science.1057726
[4]	Harrow, A.W., Hassidim, A. and Lloyd, S. (2009) Quantum Algorithm for Linear Systems of Equations. Phys. Rev. Lett., 103, 150502. http://dx.doi.org/10.1103/PhysRevLett.103.150502
[5]	Bacon, D. and van Dam, W. (2010) Recent Progress in Quantum Algorithms. Commun. ACM, 53, 84-93.
[6]	Toffoli, T. (1980) Reversible Computing. In: Proceedings of the 7th Colloquium on Automata, Languages and Programming, Springer-Verlag, London, 632-644. http://dx.doi.org/10.1007/3-540-10003-2_104
[7]	Bennett, C.H. (1989) Time/Space Trade-Offs for Reversible Computation. SIAM Journal on Computing, 18, 766-776. http://dx.doi.org/10.1137/0218053
[8]	Deutsch, D. (1989) Quantum Computational Networks. Proceedings of the Royal Society of London A, 425, 73-90. http://dx.doi.org/10.1098/rspa.1989.0099
[9]	Barenco, A. (1995) A Universal Two-Bit Gate for Quantum Computation. Proceedings ofthe Royal Society of London A, 449, 679-683.
[10]	Deutsch, D., Barenco, A. and Ekert, A. (1995) Universality in Quantum Computation. Proceedings of the Royal Society of London. Series A: Mathematical and Physical Sciences, 449, 669-677. http://dx.doi.org/10.1098/rspa.1995.0065
[11]	Di Vincenzo, D.P. (1995) Two-Bit Gates Are Universal for Quantum Computation. Physical Review A, 51, 1015-1022. http://dx.doi.org/10.1103/PhysRevA.51.1015
[12]	Lloyd, S. (1995) Almost Any Quantum Logic Gate Is Universal. Physical Review Letters, 75, 346-349. http://dx.doi.org/10.1103/physrevlett.75.346
[13]	Nielsen, M. and Chuang, I. (2003) Quantum Computing and Quantum Information. Cambridge University Press, Cambridge.
[14]	Phillip Kaye, R.L. and Mosca, M. (2007) An Introduction to Quantum Computing. Oxford University Press, Oxford.
[15]	Rieffel, E. and Polak, W. (1998) An Introduction to Quantum Computing for Non-Physicists. http://arxiv.org/abs/quant-ph/9809016
[16]	Raychev, N. (2015) Unitary Combinations of Formalized Classes in Qubit Space. International Journal of Scientific and Engineering Research, 6, 395-398. http://dx.doi.org/10.14299/ijser.2015.04.003
[17]	Raychev, N. (2015) Functional Composition of Quantum Functions. International Journal of Scientific and Engineering Research, 6, 413-415. http://dx.doi.org/10.14299/ijser.2015.04.004
[18]	Raychev, N. (2015) Logical Sets of Quantum Operators. International Journal of Scientific and Engineering Research, 6, 391-394. http://dx.doi.org/10.14299/ijser.2015.04.002
[19]	Raychev, N. (2015) Controlled Formalized Operators. International Journal of Scientific and Engineering Research, 6, 1467-1469. http://dx.doi.org/10.14299/ijser.2015.05.003
[20]	Raychev, N. (2015) Controlled Formalized Operators with Multiple Control Bits. International Journal of Scientific and Engineering Research, 6, 1470-1473. http://dx.doi.org/10.14299/ijser.2015.05.001
[21]	Raychev, N. (2015) Connecting Sets of Formalized Operators. International Journal of Scientific and Engineering Research, 6, 1474-1476. http://dx.doi.org/10.14299/ijser.2015.05.002
[22]	Raychev, N. (2015) Indexed Formalized Operators for N-Bit Circuits. International Journal of Scientific and Engineering Research, 6, 1477-1480.
[23]	Raychev, N. (2015) Universal Quantum Operators. International Journal of Scientific and Engineering Research, 6, 1369-1371. http://dx.doi.org/10.14299/ijser.2015.06.005
[24]	Raychev, N. (2015) Encoding and Decoding of Additional Logic in the Phase Space of All Operators. International Journal of Scientific and Engineering Research, 6, 1356-1366. http://dx.doi.org/10.14299/ijser.2015.07.003