A Generalized Symbolic Thomas Algorithm for Solving Doubly Bordered k-Tridiagonal Linear Systems ()
1. Introduction
The general tridiagonal matrixtakes the form:
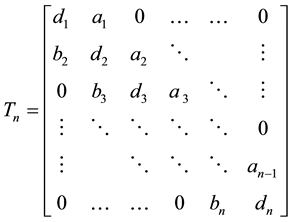(1)
Such matrices arise in many applications, such as boundary value problems, parallel computing, telecommunication system analysis, interpolation with splines and solution of differential equations using finite differences. Research area on these types of matrices is very active and has recently attracted the attention of many researchers. The interested reader may refer to [1] -[4] .
Recently, researchers have begun considering the k-tridiagonal matrix as a generalization of the special matrixin (1).
The general k-tridiagonal matrix takes the form:
(2)
For example,
(3)
The importance of such matrices could be shown clearly in the last few years. For more details see, for instance, [5] -[8] .
In this paper, we are going to focus on the doubly bordered k-tridiagonal matrix, here after will be referred to as k-DBT, which has the form:
(4)
We can hold the view that the above matrix is a natural extension of the k-tridiagonal matrix in (2).
In a partitioned form, the matrix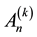 
in (4) can be written as:
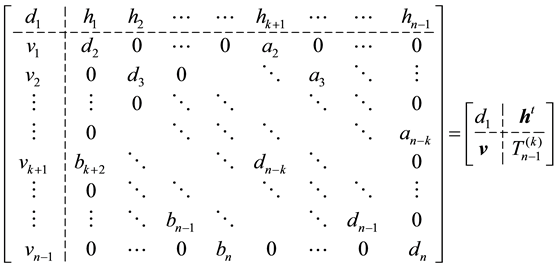(5)
where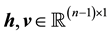 
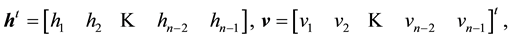and
(6)
Throughout this paper, the word “simplify” means to simplify the algebraic expression under consideration to its simplest rational form. Also,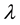 
is a formal parameter which can be treated as a symbolic name whose actual value is 0 as we will see later.
The present paper is organized as follows. In the next section, numeric and symbolic algorithms for evaluating the k-DBT determinant are constructed. The UL factorization of doubly bordered k-tridiagonal matrix is also considered. Finally, the solution of the linear system whose coefficient matrix is of type k-DBT is proposed. In Section 4, some illustrative examples are given.
2. Generalization of the DETGDBTRI Algorithm
In order to factor the k-tridiagonal matrix in (6), it is advantageous to introduce the (n − 1) quantities associated with the matrix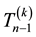 
as follows:
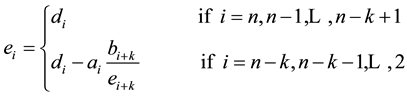(7)
Now, consider the following theorem whose proof will be omitted.
Theorem (1):
The Doolittle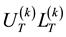 
of the matrix 
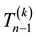takes the form:
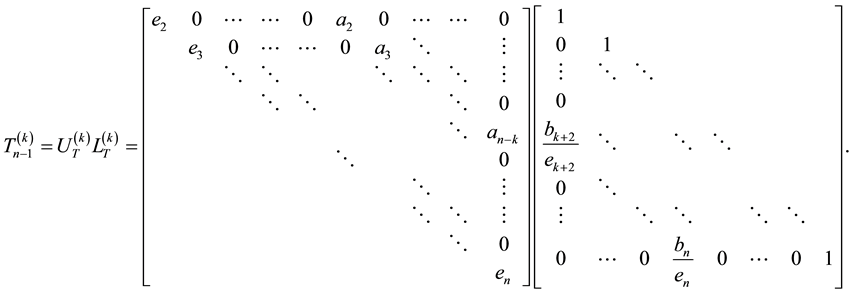(8)
At this point, it should be mentioned that the above factorization in (8) is always possible even if the matrix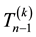 
is singular.
Armed with the partitioned form of ![]()
introduced in (4), we can construct the ![]()
factorization of this matrix as follows:
![]()
(9)
where ![]()
and ![]()
are given in (8).
By using the above equation, we see that the following four systems of equations are necessarily satisfied
![]()
(10)
![]()
(11)
![]()
(12)
and
![]()
. (13)
Solving (10)-(12) for ![]()
and ![]()
yields:
![]()
(14)
![]()
(15)
and
![]()
(16)
where ![]()
We may now formulate the following algorithm for evaluating ![]()
of the matrix ![]()
in (4).
![]()
![]()
As can be easily seen, Algorithm (2.1) breaks down if any ei = 0 for some ![]()
The following symbolic algorithm is developed in order to remove the case where the numeric algorithm fails.
![]()
The Algorithm 2.2 will be referred to as k-DETGDBTRI algorithm. It is a natural extension of the DETGDBTRI algorithm presented in [11] .
3. Solving Linear System of Equations with Coefficient Matrix of Typek-DBT
In this section, we introduce a symbolic algorithm for solving k-DBT linear systems of the form:
![]()
(17)
where ![]()
and ![]()
introduced in (4).
![]()
The Algorithm (3.2) will be referred to as k-DBTLSys algorithm. The total computational cost of the k- DBTLSys algorithm is ![]()
in terms of total number of flops, where each flop represents one of the four basic arithmetic floating point operations.
A maple code based on algorithm 3.1 is available upon request from the authors.
The following four remarks are given in order:
Remark 1. If![]()
, then we have the DETGTRI algorithm in [9] .
Remark 2. If![]()
, then we have the PERTRI algorithm in [10] .
Remark 3. If![]()
, then we have the k-DETGTRI algorithm in [8] .
Remark 4. If ![]()
for some![]()
, then we have the DBTLSys algorithm in [11] .
4. Illustrative Examples
Notice that in the following examples, blank elements in the matrices are zeros.
Example 4.1. Consider the following k-DBT linear system:
![]()
(18)
Solution: In this example, we have n = 6 and k = 3.
Applying the k-DBTLSys algorithm gives:
・ ![]()
. Hence![]()
. Thus, A is nonsingular (step 1).
・ ![]()
(step 2).
・ ![]()
(step 3).
・ ![]()
(step 4).
・ ![]()
![]()
(step 5).
The solution is![]()
.
Example 4.2. Consider the following k-DBT linear system:
![]()
(19)
Solution: In this example, we have n = 10 and k = 5.
Applying the k-DBTLSys algorithm yields:
・ ![]()
(step 1).
・ ![]()
(step 2).
・ ![]()
(step 3).
・ ![]()
(step 4).
The solution is ![]()
(step 5).
Example 4.3. Consider the following k-DBT linear system:
![]()
(20)
Solution: In this example, we have n = 14 and k = 8.
Applying the k-DBTLSys algorithm gives:
・ ![]()
(step 1).
・ ![]()
(step 2).
・ ![]()
(step 3).
・ ![]()
(step 4).
・ The solution is ![]()
(step 5).
NOTES
*Corresponding author.