Facility Location Decisions Based on Driving Distances on Spherical Surface ()
1. Introduction
The facility location problem, also known as location analysis or k center problem, is a branch of operations research and computational geometry concerned with the optimal placement of facilities to minimize transportation costs plus facilities costs while considering factors like avoiding placing hazardous materials near housing and competitors’ facilities. Poor facility location decisions can result in high transportation costs, inadequate supplies of raw materials and labor, loss of competitive advantage, and financial loss (Reid and Sanders [1] ).
The facility location problem on general graphs is NP-hard to solve optimally (Wikipedia [2] ). In the past, many facility location decisions involving distance objective functions on Spherical Surface have been approached using algorithmic, metaheuristic algorithms (Brimberg et al. [3] , branch-and-bound algorithm (Tcha and Lee [4] ), heuristic techniques (Francis and White [5] , Love et al. [6] and Farahani and Masoud [7] ), approximation algorithm (Vygen [8] and Shmoys et al. [9] ), simulation, and decomposition method (Iyigun and Ben-Israel [10] ). Ballou [11] presented an exact Center of Gravity method for facility location problems; he used iterative method to solve the facility location problems based on Euclidean distance. Several papers present general problem formulations which are involving the distance functions. The spherical facility location model studied by Katz and Cooper [12] and by Drezner and Wesolowsky [13] is a more realistic model than the Euclidean planar facility location model, especially for large regional facility location problems. Xue [14] has presented a gradient algorithm for solving the spherical facility location problem and proved a global convergence theorem for the algorithm as well as a hull property for the spherical facility location problem. Mwemezi and Huang [15] stated that current practices are dominated by Euclidean and Rectilinear models which are best suited to planar surfaces and presented an alternative distance measurement based on “great circle distance” which represents the shortest path on spherical surface. Sullivan and Peters [16] presented a new location- allocation algorithm that clusters points in a two-dimensional region into mutually exclusive groups, such that the sum of the value of a user-specified objective function calculated for each group is minimized over the whole study region. The squared distance, L-shaped distance and straight line distance functions were selected for the objective function in their example. Bespamyatnikh et al. [17] presented efficient algorithms for two problems of facility location, the first to seek a location that maximizes a weighted distance function between the facility and the sites, and the second to find a location that minimizes the sum (or sum of the squares) of the distances of k of the sites from the facility. Levin and Ben-Israel [18] presented a heuristic method to solve large- scale multi facility location problems; the method is using the authors’ single facility location method (Levin and Ben-Israel [19] ) as a parallel subroutine, and reassigning customers to facilities using the heuristic of Nearest Center Reclassification. Rodríguez-Chía and Franco [20] presented a procedure to solve the classical location median problem where the distances are measured with p-norms with p > 2. The global convergence of the sequence generated by this iterative scheme is proved by considering an approximated problem. Kotian et al. [21] developed a procedure that will solve contingent on a necessary and sufficient optimality condition, the planar k-centra location problem seeks to find a location that minimizes the sum of the Euclidean distances to the k furthest existing facilities. Iyigun and Ben-Israel [10] proposed a probabilistic decomposition method for the K facilities location problem. The problem is relaxed using probabilistic assignments, depending on the distances to the facilities. The probabilities, that decompose the problem into K single-facility location problems, are updated at each iteration together with the facility locations.
These approaches are most based on Euclidean distance or Great circle distance functions. So far, there seem to be no published papers that present the optimal or near optimal facility location decisions involving driving distance objective functions.
2. Motivation
In Figure 1, the driving distance, Euclidean distance and Great circle distance between Detroit, MI (42.331427, −83.0457538) and Cleveland, OH (41.4994954, −81.6954088) are calculated as:
Euclidean distance = 90.23 Miles as shown in Figure 2.
Great circle distance = 90.251 Miles (SAS Inc. [22] , KSU [23] and The Math Forum [24] ) as shown in Figure 3.
Driving distance = 170 Miles (Google Inc. [25] ) as shown in Figure 4.
From Figures 2-4, it is clear that the Euclidean distance and Great circle distance are not much different, the driving distance are much longer than Euclidean distance and Great circle distance. Moreover, in the U.S, as a whole, road distances between major cities are about 18% greater than the straight-line distances (Love et al. [6] ). The Euclidean distance is the “ordinary” distance between two points defined as the square root of the sum of the squares of the differences between the corresponding coordinates of the points. In Euclidean three-space (Wikipedia [26] and Wiktionary [27] ), the distance between points 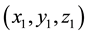 and
and 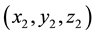 is
is
 .
.
![]()
Figure 1. Points of Detroit, MI and Cleveland, OH.
![]()
Figure 2. Euclidean distance between Detroit, MI and Cleveland, OH.
The great-circle distance is the shortest distance between two points on the surface of a sphere, measured with “Haversine” formula as (Wikipedia [28] and Movable Type Ltd [29] ).
Haversine: 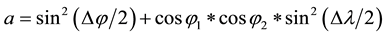
Great circle distance: 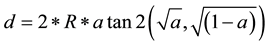
where φ is latitude, λ is longitude, R is earth’s radius (mean radius = 6371 km);
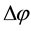 Is difference between two latitudes radians
Is difference between two latitudes radians
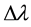 Is difference between two longitudes radians
Is difference between two longitudes radians
![]()
Figure 3. Great circle distance between Detroit, MI and Cleveland, OH.
![]()
Figure 4. Driving distance between Detroit, MI and Cleveland, OH.
where 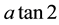 is the arctangent function with two arguments. In terms of the standard arctan function, whose range is
is the arctangent function with two arguments. In terms of the standard arctan function, whose range is , it can be expressed as follows:
, it can be expressed as follows:
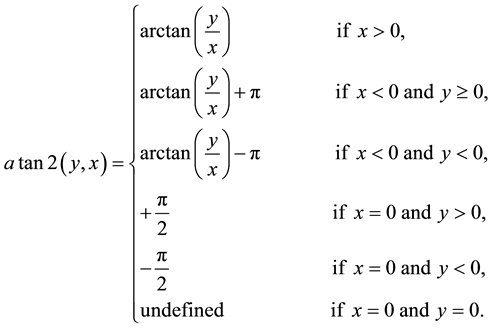
Microsoft C# uses Math. Atan2(y, x) function to calculate Atan2(y, x)
Several papers have applied Weiszfeld [30] iterative method to solve spherical facility locations problems involving Euclidean distance and Great circle distance. Katz and Cooper [12] proposed the following closed form iteration formula for solving the spherical facility location problems. There are no any iteration formulas in relation to driving distances.
For Euclidean distance 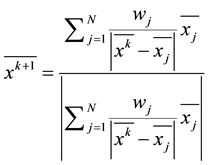
For Great circle distance
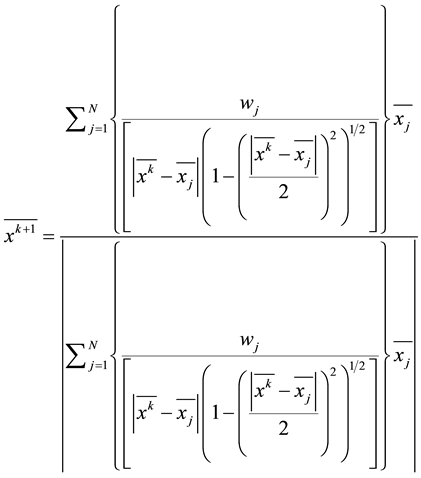
So far, there seem to be no published papers that have applied iterative method based on driving distances. Katz and Cooper [12] stated that if points are widely separated, the difference between Euclidean and Great circle distances may be significant, and this may lead to significant variations in the location of the corresponding optimal source points. Aykin [31] stated that the assumption that the earth can be considered as a plane is not appropriate and introduces error if the demand points are spread over a relatively large region.
These facts motivate me to do research and propose an approach for facility location decisions based on driving distances on spherical surface using heuristic technique and helps companies assess the optimal locations of facilities. In particular, the following problem is worth pursuing:
Given:
・ The location of each destination in terms of their co-ordinates
・ The requirement at each destination
・ A set of shipping costs for the region of interest
To determine:
・ The optimal number of facilities
・ The location of each facility
The optimal facilities locations are those that minimize the driving distances related costs plus facilities costs.
The implementation method proposed in this paper is carried out by using heuristic iterative approach. This paper is organized as follows: Sections 1 is Introduction. Section 2 states the motivation for researching this paper and proposes a framework and algorithm. In Section 3, the facility locations decisions implementation of the proposed framework and algorithm is carried out using a hypothetical case study. In conclusion, Section 4 summarizes this study and outlines its contributions and future research.
3. Implementation Methodology for Facility Location Decisions
3.1. Algorithm
The algorithm of this paper is to develop a method to determine the optimal facility location to minimize the sum of facilities cost and the sum of the volume of goods at a destination multiplied by the transportation rate to ship to the destination multiplied by the Google maps driving distance based on the following assumptions:
1) The good of every destination points can be transported in one time, and the velocity is not changed.
2) The one destination point is only served by one warehouse.
3) The cost is related the length from the warehouse to the destination point, the transport conditions are not considered. Transportation cost is related to the distance only. The transportation cost equals the distances traveled times a fixed price per unit, distance.
4) The warehouse locations are located at populated places (cities/towns).
5) All service facilities are identical.
6) Each destination point wishes to minimize the cost of acquiring the product.
7) The company treats each cluster independently.
The strategy of the algorithm involves the following steps:
Step 1. Generate Google maps driving distance matrix from the set of destination locations’ latitudes/longi- tudes.
Step 2. Perform K means clustering based on the destination locations driving distance matrix to generate K clusters.
Step 3. Calculate starting point of facility location for each cluster using Center of Gravity method and sets as current facility location.
Step 4. Construct the circle whose radius is the maximal Google maps driving distance from current facility location.
Step 5. Query the populated cities within the circle constructed in Step 4.
Step 6. Calculate the cost from each queried city to all destination locations, the queried city with the smallest cost will become new current point.
Step 7. Repeat steps 4 to 6 until no new current point can be found.
Step 8. Randomly select several cities points as current points and perform steps 4 to 6 to show that the local optimal facility location is the global optimal or nearly global optimal facility location.
Step 9. Calculate the total cost for each set of clusters.
Step 10. Perform another set of clustering if desired and repeat Steps 3 to 9 until no clustering is desired.
Step 11. Compare the cost of each set of clusters; select the set of clusters with the minimal total cost and optimal facility locations.
Figure 5 shows the flowchart of Facility location decisions process.
In Figure 5, the implementation details are described as follows and a lot of C# programs have been written for the implementation (Source codes are available from the author).
Step 1. A Google maps driving distance matrix is generated as a distance data set and used as input in SAS
![]()
Figure 5. Flowchart of facility location decisions process.
Clustering procedure. A C# program is written using the Google Maps API (Google Inc. [25] ) to create a driving distance matrix that will be used as input in SAS Clustering procedure.
Step 2. After driving distance matrix is generated, the next step is to cluster the cities based on Driving distances. This paper will use SAS Clustering procedure (SAS Inc. [32] ) to cluster for the cities. TYPE = DISTANCE data set can be used as an input data set to PROC MODECLUS or PROC CLUSTER (SAS Inc. [32] ). PROC CLUSTER ignores the upper triangular portion set and assumes that all main diagonal values are zero, even if they are missing. PROC MODECLUS uses the entire distance matrix and does not require the matrix to be symmetric. Since the driving distance matrix data set is not necessary symmetric, the MODECLUS Procedure is used in my paper to cluster the cities.
Step 3. Calculate the initial starting facility location centers for each cluster. Several quantitative techniques (Heizer and Render [33] , Reid and Sanders [1] and Pearson [34] ) have been developed to assist initial site selection. This paper uses Center of Gravity method (Ballou [11] , Geo Midpoint [35] , Chen and He [36] , Heizer and Render [33] and Kuo and White [37] ) to calculate the starting point of facility location. The Center of Gravity method assumes that the cost is directly proportional to distance and volume shipped, inbound and outbound transportation costs are equal, and it does not include special shipping costs for less than full loads. Using latitude and longitude coordinates might be helpful (Heizer and Render [33] and Chase et al. [38] ) to calculate the initial facility location centers for each cluster. This paper assumes a spherical earth and sea-level points, the following formula is used to perform spherical coordinate conversion from latitude/longitudes to Cartesian coordinates for each destination location. The formula is much more complex for ellipsoidal earth (Ligas and Banasik [39] ).
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
where r is the earth’s radius.
Next, compute weight volume of good multiple by shipping cost for each location
![]() (4)
(4)
where ![]() is the volume of good to be shipped to location i,
is the volume of good to be shipped to location i, ![]() is the shipping rate per unit of good to location i.
is the shipping rate per unit of good to location i.
The initial center of gravity ![]() and
and ![]() are calculated as
are calculated as
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
Then, the initial starting Cartesian coordinates are converted to latitude/longitudes points as input for Step 4.
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
Step 4. Calculate the driving distances from the current point calculated in Step 3 to each destination location of each cluster using the Google Maps API (Google Inc. [25] ).
Step 5. Search the optimal facility locations. All distances are calculated using the Google maps driving distances. Let the starting point be the current point calculated in Step 3. Use the maximal Google maps driving distance calculated from Step 4 as radius of current point. The cities are queried in a circular pattern around the current point at a maximal driving distance. This paper utilizes a function in Map Suite WinForms Desktop free trial Edition (Thinkgeo LLC [40] ) and a populated places database of Natural earth data source (Natural Earth [41] ) to query all cities with the maximal driving distance of current location point.
Step 6. Calculate the total cost between each queried city to all destinations locations within each cluster. Compare the cost of each queried city and find the city which has minimal cost. If any of the queried cities has a new minimal cost, then that city will become new current point and go back to repeat steps 4 to 6 until no new smallest cost can be found. Otherwise, If none of the queried cities has a new minimal cost, then the current city becomes the optimal facility location for that cluster.
Step 7. Randomly select several points (Hillier and Lieberman [42] ) and perform Steps 5 to 6 to show that the local optimal facility location obtained in Step 6 is the global optimal or nearly global optimal facility location.
Step 8. Calculate the total cost for all clusters in the cluster set.
Step 9. Generate other clusters if desired and repeat steps 3 to 8 to calculate the total cost for all clusters in the cluster set until no clustering is desired.
Step 10. Select the set of clusters which has the minimal total cost, the optimal facilities locations will be the cities found in Step 7.
3.2. Methodology Implementation
Based on the formulas from several papers (Rodriguez-Chia and Valero-Franco [20] , Mwemezi and Huang [15] , Katz and Cooper [12] and Litwhiler and Aly [43] ), this paper formulates the model as follows:
![]() (11)
(11)
Subject to: ![]()
![]()
![]()
![]()
![]()
![]()
![]() = total # of destinations
= total # of destinations
where ![]() = Total cost for m clusters
= Total cost for m clusters
![]() = destination locations for each cluster
= destination locations for each cluster
![]() = Volume at destination i in cluster k
= Volume at destination i in cluster k
![]() = Transportation rate to destination i in cluster k
= Transportation rate to destination i in cluster k
![]() = Driving distance from the facility to be located to destination i in cluster k
= Driving distance from the facility to be located to destination i in cluster k
![]() = facility cost at each cluster k
= facility cost at each cluster k
Given the assumptions described in Section 3.1. We search the optimal facility to minimize the sum of facilities cost and the sum of the volume at a destination multiplied by the transportation rate to ship to the destination multiplied by the driving distance for the cluster.
3.3. Hypothetical Case Study
ABC Company has 88 market cities located in Midwest, USA; the company seeks to build several warehouse centers to ship their goods to those markets to serve their customers. Assume that travel originates and ends at the warehouse centers. The coordinates (Latitude/Longitudes) of each market location and volume of goods and transportation rate for each market location are provided. The facility cost is 100,000.00. The goal is to minimize the sum of facilities costs and the sum of transportation costs. Figure 6 is the graphical map of 88 major market cities.
Appendix A is the coordinates (Latitude/Longitudes) of each market location and volume of goods and transportation rate for each market location. The facility cost is 100,000.00.
Step 1. Converting major cities data to driving distance matrix
Use coordinates (Latitude/Longitudes) provided in Appendix A as inputs to create a driving distance matrix that will be used as inputs to MODECLUS clustering procedure in SAS. Appendix B is part of Google maps distance matrix of 88 Midwest major market cities.
Step 2. Clustering techniques
Set the driving distance matrix in Appendix B as input, the SAS MODECLUS Procedure is used to perform clustering for the cities. Table 1 is cluster output from SAS code:
Proc modeclus data = work. Driving Data (TYPE = DISTANCE) list m = 1 k = 3; id location; run;
Figure 7 is the map of 14 clusters for the 88 major market cities located in Midwest, USA.
The following steps 3 to 7 are performed for cluster 1.
Step 3. Using equations from (1) to (7), the initial center of gravity for cluster 1 is calculated as in Table 2 and shown in Figure 8.
Using equations (8) to (10), the Latitude and Longitude of Center of gravity is calculated as 41.5995134613, −96.62241872.
Step 4. Table 3 shows the driving distances from current point to each market city location.
Step 5. The surrounding cities/towns with radius of maximum driving distance (157 miles) from Center of gravity are queried with Map suite tools and Natural populated placed data, the queried results are show in Table 4 and the map is shown in Figure 9.
Step 6. Table 5 shows the costs from each city to all market cities locations. From Table 5, the Depot 15 has the smallest cost, and then Depot 15 (Omaha, NEB) will become new current point. The driving distances from new current point to each market city location are calculated as in Table 6. The maximum driving distance is 190 miles.
![]()
Figure 6. Map of 88 major market cities located in Midwest, USA.
![]()
Figure 7. Map of 14 clusters for the 88 major market cities in Midwest, USA.
![]()
Figure 8. Cluster 1 with initial starting point- center of gravity (Scribner, NE―Green square).
![]()
Figure 9. Cluster1 with Cities (Blue stars) of radius of maximum driving distance of current point (Scribner, NE―Green square).
Repeat Steps 4, 5, & 6. The surrounding cities/towns with radius of maximum driving distance (190 Miles in Table 6) from Depot 15 (Omaha, Nebraska, USA) are queried with Map Suite tools and Natural populated placed data, the queried results are show in Figure 10.
Table 7 is the queried cities within the radius of maximum driving distance (190 miles) from current point. Figure 10 is the map with queried cities of radius of maximum driving distance of current point. Table 8 shows the cost from each city to all market cities locations.
From Table 8, use Depot 23 as the current point (Omaha, Neb.) and repeat steps 4 to 6, there is no new smallest cost can be found.
![]()
![]()
Table 1. Modeclus cluster procedure with m = 1, K = 3.
![]()
![]()
Table 2. Center of Gravity for cluster 1.
![]()
Table 3. Driving distances from current point to each market location.
![]()
Table 4. The queried cities within the radius of maximum driving distance from current point Radius of 157 miles.
Step 7. Randomly select several points (Hillier and Lieberman [42] ) and perform Steps 5 to 6 to show that the local optimal facility location obtained in Step 6 is the global optimal or nearly global optimal facility location. Tables 9-12 show the results of each randomly selected city to all market cities locations. It is concluded that the global optimal facility location is the city found in Step 6. The optimal facility location will be Omaha, Nebraska shown as in Figure 11.
Using the same steps for cluster 1, the optimal facility locations for clusters 2 to 14 are calculated and shown as from Figures 12-24.
The total cost for these 14 clusters is calculated using equation (11) and shown as follows:
![]()
Table 5. Cluster1 costs from queried cities to market locations-iteration1.
![]()
Table 6. Driving distances from current point (Omaha, NE) to each market location.
3.4. Results: Driving Distance vs. Euclidean Distance and Great Circle Distance
With the data in Table 13, I use the steps described in Section 3.2 to search the optimal facility location based on driving distance vs. Euclidean distance and Great circle distance. As the results shown in Figures 25-27, the optimal facility location based on driving distance is different from the optimal facility location based on Euclidean distance and Great circle distance.
With the data in this case study, I use the steps described in Section 3.2 to search the optimal facility location based on Euclidean distance and Great circle distance. It is found out that the optimal facilities locations for Clusters 1 to 14 are the same when the distances are based on driving distance, Euclidean distance or Great circle distance. For examples, Cluster 3 (see Figure 13 and Figure 28), Cluster 4 (see Figure 14 and Figure 29), Cluster 5 (see Figure 15 and Figure 30) and Cluster 10 (see Figure 20 and Figure 31) have the same optimal facilities locations.
However, the above results reveal that if the driving distance is much longer than Euclidean distance or Great circle distance because there are lakes, rivers between locations (see Figures 2-4 and Figure 25), the optimal facility location based on driving distance will be different from the optimal facility location based on Euclidean
![]()
Table 7. The cities within the radius of maximum driving distance from current point (Omaha, NE).
![]()
![]()
Table 8. Cluster1 costs from queried cities to market locations―iteration 2.
![]()
Figure 10. Cluster1 with cities (Blue stars) of radius of maximum driving distance of current point (Omaha, Neb.)
distance and Great circle distance. The facility location decision based on driving distances is a practical approach. In regard to transportation cost, the driving distances in the presence of geographic barriers should be taken into consideration in facility location decisions.
3.5. Compare the Total Cost of Different Set of Clusters
Now, this paper uses MODECLUS Procedure to get different set of clustering and select the best set of clusters.
Table 14 is clustering output of 11 clusters from SAS code with m = 1, k = 4.
Table 15 is clustering output of 9 clusters from SAS code with m = 1, k = 5.
From equation (11) ![]()
![]()
Figure 11. Cluster 1 with optimal facility location (Omaha, Neb.―Brown triangle).
![]()
Figure 12. Cluster 2 with optimal facility location (Kansas City, MO―Brown triangle).
![]()
Figure 13. Cluster 3 with optimal facility location (Akron, OH―Brown triangle).
![]()
Figure 14. Cluster 4 with optimal facility location (Milwaukee, WI―Brown triangle).
![]()
Figure 15. Cluster 5 with optimal facility location (Flint, MI―Brown triangle).
![]()
Figure 16. Cluster 6 with optimal facility location (Lima, OH―Brown triangle).
![]()
Figure 17. Cluster 7 with optimal facility location (Springfield, IL―Brown triangle).
![]()
Figure 18. Cluster 8 with optimal facility location (Dayton, OH―Brown triangle).
![]()
Figure 19. Cluster 9 with optimal facility location (Mooresville, IN―Brown triangle).
![]()
Figure 20. Cluster 10 with optimal facility location (Detroit, MI―Brown triangle).
![]()
Figure 21. Cluster 11 with optimal location (Rochester, MN―Brown triangle).
![]()
Figure 22. Cluster 12 with optimal facility location (Jamestown, ND―Brown triangle).
![]()
Figure 23. Cluster 13 with optimal location (Carbondale, IL―Brown triangle).
![]()
Figure 24. Cluster 14 with optimal facility location (Hutchinson, KS―Brown triangle).
![]()
Figure 25. Optimal facility location (Milwaukee, WI) based on driving distance.
![]()
Figure 26. Optimal facility location (Fond du Lac, WI) based on Euclidean distance.
![]()
Figure 27. Optimal facility location (Fond du Lac, WI) based on Great circle distance.
![]()
Figure 28. Cluster 3 with optimal facility location (Akron, OH―Brown triangle) based on Euclidean distance or Great Circle distance.
![]()
Figure 29. Cluster 4 with optimal facility (Milwaukee, WI―Brown triangle) based on Euclidean distance or Great Circle distance.
![]()
Figure 30. Cluster 5 with optimal facility location (Flint, MI―Brown triangle) based on Euclidean distance or Great Circle distance.
![]()
Figure 31. Cluster 10 with optimal facility (Detroit, MI―Brown triangle) based on Euclidean distance or Great Circle distance.
![]()
Figure 32. 9 clusters with 9 optimal facilities locations (Brown triangles).
![]()
Table 9. Cluster 1 costs from queried cities with Sioux City, Iowa as COG to market locations.
![]()
![]()
Table 10. Cluster 1 costs from queried cities with Council Bluffs, Iowa as COG to market locations.
![]()
Table 11. Cluster 1 costs from queried cities with Norfolk, Nebraska as COG to market locations.
Table 16 is the summary of total cost for each set of clusters. From the result shown in Table 16, it is con- cluded that the set of 9 clusters with 9 optimal facilities locations are selected shown as in Figure 32.
4. Conclusions and Future Research
Facility location decisions play an important role in the strategic planning and design of logistics/supply chain network. Well-planned location decisions enable the efficient flow of materials through the distribution system,
![]()
Table 12. Cluster 1 costs from queried cities with Yankton, South Dakota as COG to market locations.
![]()
Table 13. Six locations with volume and transportation rate.
and lead to decreased costs and improved customer service. This paper has focused on the implementation of facility location decisions based on driving distances on a sphere surface. Two objectives have been achieved inthis paper. Given the location of each destination in terms of their coordinates, the requirement at each destination and shipping costs for the region of interest, the proposed methodology in this paper is able to determine the
![]()
![]()
Table 14. Modeclus cluster procedure with m = 1, K = 4.
![]()
![]()
Table 15. Modeclus cluster procedure with m = 1, K = 5.
![]()
![]()
Table 16. Summary of total cost for each set of clusters.
11 clusters:
9 clusters:
optimal location of each facility and helps companies assess the locations of facilities. The second object is to establish terminology and an analytical framework for locating optimal facility in perspective. In regard to transportation cost, the driving distance in the presence of geographic barriers should be taken into consideration in facility location decisions. The proposed method in this paper has shown very promising results. The potential benefits of my work include:
• The driving distance measure can be applied to transportation problems, travelling sales person problems, and etc., in Operations Research (OR) study.
• This proposed method can be extended to facility location decisions based on Euclidean distance and Great circle distance functions.
• The framework and methodology proposed in this paper can be applied to improve the management of logistics/supply chain system decisions and planning to make smooth flow throughout the supply chain.
This paper has focused on the facility locations in the region of Midwest, USA. Markets and competition are increasingly global, further research work could include investigation in the process of international facility locations around the world. Therefore, a global driving distance model within and/or outside the US is needed for further work. In addition to qualitative analysis, some factors affecting locations need to be considered, such as labor costs and availability, including wages, productivity, attitudes, age, distribution, unionization, and skills, State and local government fiscal policies (including incentives, taxes, unemployment compensation), proximity to customers, population distribution, quality-of-life issues (education, cost of living, health care, sports, cultural activities, housing, entertainment, religious facilities, etc.).
This paper assumes a spherical earth and uses equation (1) to (7) to calculate initial center of gravity and equation (8) to (10) to convert Cartesian coordinated to latitude/longitudes. Further research could be done on assumption of ellipsoidal earth. Also, further research work can be suggested to apply this proposed methodology on capacity facility location decisions problems.
Geographic Information Systems (GIS) also helps in location analysis; further research work can be approached using GIS instead of Google maps.
Finally, since uncertainty associated with future conditions exists in real world, facility location decisions must account for the inherent uncertainty. This is an area worthy of additional research too.
Acknowledgements
The author is very grateful to the editor and anonymous referees for their valuable comments and suggestions on the earlier version of the manuscript.
Appendix A: Coordinates (Latitude/Longitudes) and Volume of Goods and Transportation Rate for Each Market City Location
Appendix B: Google Maps Distance Matrix of 88 Midwest Major Market Cities