Thermodynamic Equilibrium of the Saturated Fluid with a Free Surface Area and the Internal Energy as a Function of the Phase-Specific Volumes and Vapor Pressure

Albrecht Elsner

Am Mühlbach 14, D-85748, Garching, Germany.

DOI: 10.4236/eng.2015.79053                

Abstract

This study is concerned with describing the thermodynamic equilibrium of the saturated fluid with and without a free surface area A. Discussion of the role of A as system variable of the interface phase and an estimate of the ratio of the respective free energies of systems with and without A show that the system variables given by Gibbs suffice to describe the volumetric properties of the fluid. The well-known Gibbsian expressions for the internal energies of the two-phase fluid, namely for the vapor and for the condensate (liquid or solid), only differ with respect to the phase-specific volumes and . The saturation temperature T, vapor presssure p, and chemical potential are intensive parameters, each of which has the same value everywhere within the fluid, and hence are phase-independent quantities. If one succeeds in representing as a function of and , then the internal energies can also be described by expressions that only differ from one another with respect to their dependence on and . Here it is shown that can be uniquely expressed by the volume function . Therefore, the internal energies can be represented explicitly as functions of the vapor pressure and volumes of the saturated vapor and condensate and are absolutely determined. The hitherto existing problem of applied thermodynamics, calculating the internal energy from the measurable quantities T, p, , and , is thus solved. The same method applies to the calculation of the entropy, chemical potential, and heat capacity.

Keywords

Fluid with Free Surface Area, Solution of Gibbs’s Internal Energy Equations, Chemical Potential Expression, Calculation of Entropy and Heat Capacity

1. Introduction

We are concerned here with electrically and magnetically neutral single-component matter under steady-state equilibrium conditions which are thermodynamically defined in the immediate vicinity of the critical point and below it. Between the critical gas temperature 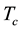and the triple-point temperature (if it exists) the gas mass M is structureless and homogeneously distributed in the vessel volume V. It is assumed that M has the critical density. Below the critical point, M is decomposed as condensed mass with the density in the sub-volume and as vapor mass with the density in the sub-volume. This gas mass in thermodynamic equilibrium existing in two phases is called a saturated fluid. As thermodynamic theory teaches, the only independent variable of the saturated fluid that can be chosen is the saturation temperature T, since the other field variables possible, viz. vapor pressure p and chemical potential, are unique functions of T.

The critical point, from the experimental perspective, is the first occurrence or vanishing of a free surface A observed in V, which separates the volumes and from one another. By variation of T and M or V and observing the occurrence of A, one can define and measure the critical values v, , and.

The work in Section 2 is concerned with describing the thermodynamic equilibrium of the real gas. The stationary equilibrium of M in V is known from Gibbs to be expressed by the fundamental equation which reproduces the functional relation among V, M, and the properties of the fluid, viz. entropy S, internal energy U, and free energy.

Section 3 firstly treats the equilibrium of the two-phase fluid without an internal free surface, i.e.. The distributions of the masses and in and are given as functions of T. Then the equilibrium in the case is discussed where there is a third fluid phase, called the interface phase. To it is assigned the free interface energy, which is identified with (surface tension), so that the ratio can be numerically estimated. Estimation and discussion of the role of A as system variable show that the system variables given by Gibbs suffice to describe the volumetric properties of the fluid with and with- out a free surface area.

In Section 4, it is reminded that the entropy and energy functions S, , and and also U, , and assigned to the masses M, , and are absolute temperature functions with thermodynamic zeros. This result, which can be deduced from internal energy functions being subject to Nernst’s theorem at absolute zero, is noteworthy, because the said quantities have been treated in Applied Thermodynamic Theory for more than a century as temperature functions with arbitrarily specified constants.

Finally, in Section 5, the central task of this work, viz. finding an explicit thermodynamic expression for in, is tackled and then solved in Section 6. The energy functions u, , , , , and, and the heat capacities c, , and can then be calculated from the measurable quantities, , and.

By means of the expression given for the volume function many thermodynamic relations are verified in the Appendix, this in turn being evidence for the correctness of the volume function used.

2. Description of the Thermodynamic Equilibrium of the Real Gas

Thermodynamics uses intensive and extensive quantities to describe the equilibrium state of the gas mass M enclosed in the volume V. An intensive property of the gas is the same everywhere in the volume and is therefore independent of the mass. Intensive equilibrium state quantities are the temperature T, pressure p, and chemical potential. They are defined by the first partial derivatives of extensive quantities [1] , e.g., the internal energy U, which according to the fundamental equation is a function of entropy S, volume V, and mass M [2] :

(1)

Variations in the extensive quantities S, V, and M lead to variations in the intensive quantities T, p, and [2] as follows:

(2)

By means of Maxwell’s relations [2] , ,

, , , and

the differentials (2) can be written in the form

(3)

For the single-component gas the well-known Gibbs-Duhem relation between the intensive quantities in dif- ferential form reads [2] :

(4)

Explicit writing gives

(5)

Variations in S, V, and M can be performed independently of each other. For dV = 0 and dM = 0 one thus has or

. Applying the identity

, the entropy relation can be written as.

Using the Maxwell relations and, one arrives at the

Gibbs-Duhem form of the entropy:

(6)

With and dM = 0 one obtains, whereas the conditions

and give.

In the following, the properties of the real gas are investigated under the condition of constant mass M in given volume V. The entropy thus has the form (6). The internal-energy expression immediately follows from

the fundamental equation, i.e. or

(7)

According to relations (6) and (7), the entropy and internal energy of the gas mass are defined by the temperature derivatives of the intensive quantities and p and the quantities M and V. The gas volume V has the significant property that it is proportional to the gas mass M since the gas of mean density assumes the equilibrium-state volume. The entropy S and internal energy U are thus quantities that are proportional to M and hence absolute quantities [3] . As mentioned above, extensive and intensive quantities, both of which are given with absolute figures, are used for describing the emquilibrium properties of the gas, no matter which gas phases exist.

3. Two-Phase Equilibrium without and with a Free Surface Area

For every real gas there is a certain temperature, called critical temperature, at which the gas mass M decomposes into a low-density vapor-phase mass and a high-density condensed-phase mass (liquid or solid). The masses and are located in different subvolumes and, separated from one another by a free interface area A. If, the first occurrence of A in V defines the critical volume v and, i.e. the critical point of the gas, which for temperatures is termed as a saturated fluid. Ignoring the existence of A, this fluid has the following properties:

(8)

The relation states that the quantity X is proportional to the mass M, which means that each of the functions X (gas volume V, entropy S, internal energy U, free (Helmholtz) energy, enthalpy, Gibbs energy, and heat capacity) ensures its uniqueness, has absolute value due to its thermodynamic zero, and is numerically interrelated to one another [3] .

The decomposition of mass M into and below the critical point is intrinsicly described by [3]

(9)

Taking, and, Equation (9) gives

(10)

It is seen, because of, that the mass ratios are functions of v and T.

The proof of is as follows: The positive functions and

are related by and. For the functions and con- verge from above and below to the same limiting value. This yields or.

Then equation represents the relation between the masses and specific volumes on incipient decomposition. With decreasing system temperature, more and more vapor particles con- dense into the liquid phase, i.e. the mass ratio becomes less than 1 and decreases with decreasing

temperature: and for.

If one investigates the temperature dependence of the volumes and between the critical point and absolute zero, one can generally ascertain that the volume variations are smaller than those of the masses and take opposite directions. From one obtains and

, while from it follows that

and. Since for real gases the ratio takes values between 1.5 and 3, with a jump occurring at the triple point. The following relations are valid:

(11)

Evaluation of relations (10) and (11) is given by means of published volume data for argon in Figure 1.

Let us now turn to the problem of thermodynamic treatment of the physics of the free interface surface A. As stated, the existence of A affords the possibility of distinguishing in V between two fluid phases of different mass densities and and defining the critical point. Thermodynamic theory teaches that the intensive quantities T, p and have the same value everywhere in V, i.e. in the interface layer as well, in which the density decreases from to. If the length of this decrease is denoted by the distance, the volume can be assigned to the interface layer, in which the interface mass is located, where it holds that and with. The fictitious quantities and, however, cannot be thermodynamically calculated, whereas both the minimum surface expansion A, resulting from intermolecular and acceleration forces, and the surface tension, which is a measure of the effectiveness of these forces at the surface, are measurable quantities, being a positive quantity [5] . The force resulting from these two yields the direction of the surface normal of A. The expansion of A depends on the shape of the vessel V. If, for example, the shape of V is chosen such that arbitrary rotation about the center of gravity of M changes the location of the interface, i.e. the height and expansion, the values of p and as measures of the energy density in and A remain unchanged, but the distribution of

Figure 1. Mass ratio and volume ratio of argon as functions of the temperature. Data and from Ref. [4] .

the interface mass in the newly formed volume is changed and this can also be reversed isother- mally and isobarically, since the free energy measures the mechanical work done. On the other hand, the redistribution of the fluid mass is a result of the changed gravitation potential in V and this can, in principle, be determined as potental energy from the height differences of A before and after rotation and hence be thermodynmically expressed by the difference in the free energy F. Thus A can be regarded as an external thermodynamic variable, and the product is measurable and constitutes a thermodynamic quantity.

Independently of prehistory, it holds for the saturated fluid that if the condition for forming a free surface between the liquid and vapor phases is given, then there is an interface particle layer, which represents a new equilibrium state described by a minimum internal energy U and simultaneously a maximum entropy S. Hence formation of the free interface surface A lowers the free energy of the fluid, F. This situation is formally taken into account by introducing the phase “interface” in keeping with the additive property of a variable X in addition to the phases “vapor” and “condensate” [6] :

(12)

The energy term is interpreted as free interface energy and described by the function; the newly introduced function is interpreted as surface energy, and the function as surface entropy. These func- tions represent reversible interface quantities of the free surface A which vanish at and also at because and.

Then the enlarged Gibbs relations (6) and (7) read [6]

(13)

Figure 2 shows the temperature dependence of, , and for argon. In turn, these functions multiplied by A represent the area-contributions to the negative internal and free energies and positive entropy of the saturated fluid.

In order to put the interface quantity in thermodynamic relation to the above-mentioned quantities and, is set equal to. Assuming, and a mean in-

terface density, one obtains, because of, a functional relation between surface

tension and interface quantities,

(14)

which, however, remains numerically indeterminable owing to the hypothetical length. In turn, relation (14) allows the qualitative statement that is continuously increasing from 0 at to values of order at (see Figure 2, Figure 4 and Figure 8).

The relative energy contribution of an interface quantity to the respective system quantity depends on the ratio of the numbers of interacting particles in the interface volume and system volume V, i.e. , and is therefore extremely small. Despite the smallness of the order and less [7] [10] , surface effects play a great role in nature and technology. The smallness of an interface quantity shows, on the other hand, that ignoring it when studying volume properties of the fluid is completely justified. As the existence of a surface A does not change the mass M and volume V, the property of U, S, and F being extensive quantities is maintained.

4. The Thermodynamic Zero of Thermodynamic Functions

According to the Gibbsian energy Equation (7), the mass- and phase-specific internal energies of the saturated

Figure 2. Analysis of free-surface quantities. From fitted published surface tension data of argon [8] [9] and setting equal to the area-specific free energy, i.e., one gets the area-specific surface energy and the area-specific entropy. It holds that. Each of these functions vanishes at.

fluid are interrelated as follows:

(15)

Since and for, one has and

for and at. By virtue of Nernst’s theorem

at absolute temperature zero it holds that,

and

The vanishing energy value gives the argument for binding the thermodynamic value 0 to the relations. The conditions ex- clude, however, the validity of the relations, , and for, and admit only. Thus the unique solution for the internal energies is found:

(16)

Relations (16) say that the internal vapor energy is not negative and the internal fluid energy u is equal or greater than the internal condensed matter energy and the two are not positive. At the crtical point, each of these energies vanishes.

In keeping with W. Gibbs [1] , it is hypothetically asserted in the literature (e.g. [11] -[13] ) that the temperature dependence of u, , and is determined only up to an arbitrary constant a, i.e. and. On the contrary, because of Nernst’s theorem the relations (16) state that and thus confirm the universality of the Gibbsian entropy and energy expressions (6) and (7), which are given in thermodynamic terms without any shifts.

Moreover, some thermodynamic relations are mentioned in relation to the thermodynamic value 0:

(17)

The chemical potential functions are given in explicit form as energy functions:

(18)

Setting relations (9) yield

(19)

The critical value is finite for and divergent for.

5. The Unsolved Problem in Applied Thermodynamics

Endeavors to publish data of the energy and entropy functions and are prominent in the current literature. Since the numerical solution and the consequence, viz., are known in the literature [3] , it is obvious from relations (15) that the task of finding an explicit thermodynamic expression for for should be tackled. Calcula- tion of now occupies the center of interest in applied thermodynamics.

Solution of the problem is not trivial, as the following solution ansatzes for the volume function

will show. The specified lower limit does not constitute a solution for

Temperatures T < T_c, because this ansatz leads to a value of the condensate at absolute zero of, whereas is the correct result there. The upper limit is no solution of either, because in this case the function would vanish identically.

In order to find a solution for, the obvious course is to consider the equilibrium relation that follows from relations (15):

(20)

As the equations show, what is needed is a thermodynamic expression for. For temperatures, the limits of the energies in relation to the evaporation energy are known [3] :

(21)

Van der Waals showed that the volumes can be represented as functions of. (Here is expanded as a power function of the temperature distance from the critical point, where the temperature distance between and 0 is given by the expansion parameter passing through the values from 0 to 1). Thus the functions can be analogously represented as functions of:

(22)

At the critical point one gets and, , and at absolute zero

one gets and,. The success of the van der Waals representation of as functions of consists in giving a relation between and. As long as is regarded as an independent variable, the ansatzes (22) merely state that the functions scale at the critical point as the function. If, however, every value can be assigned a certain temperature value T, the values are fixed. Therefore, in Equation (22) is replaced as follows in order to characterize the phase of the energy functions with temperature-dependent phase-specific functions and:

(23)

Taking the difference yields the condition and calculating and gives

(24)

Appropriate as variable of the phase functions is the volume ratio in the vapor and liquid phases, , because this numerical ratio at the same time inter-relates the effects of the interaction forces between the fluid particles in the respective phases. Just as the subscript v or l suffices to describe the phase of an energy function, a phase function is adequately described either by the subscript or again or else just by specifying the variables and z. The definition of z and phase functions and is thus

(25)

A phase function represents a state function in that it contains information on the density and internal energy distribution in the respective phase. This becomes particularly clear when the ratio is formed,

which can also be expressed by the ratio. It holds that at absolute zero and

that at the critical point, whence. Furthermore, it holds that

and, and hence; it thus follows that

or, i.e. the function increases strictly

monotonically as z and, at the same time, the function decreases strictly monotonically. The domain of

the function is, because the value tends to zero when the value of z grows beyond all limits.

What is now needed is a solution of the functional equation for with subsidiary conditions:

(26)

The general solution is of the form

(27)

Proof: Suppose being a real (composed) function, for. One has

with

and.

Of the mathematical solutions possible the following (with at the critical point) is selected:

(28)

This equation yields the physically relevant solution. It is noted that the solution ρ according to Equation (28) can be represented as a convergent Taylor series. Figure 3 shows the functions and.

Before tackling the important investigation of the uniqueness of this solution, one should consider the method of solution that uses the variable. Equations (23) and (24) yield

(29)

Admittedly, the latter equation does not yield a direct solution, but it does give the interesting dependence in the form of with the solutions and. The equality of and only exists at the critical point and marks the start of the single-fluid phase.

With and the variable has the following dependence on z:

Figure 3., , and as functions of z for.

(30)

and one calculates for and for.

According to Equations (20) and (22) one obtains

(31)

Inserting the solution for in Equation (31) gives the symmetric form:

(32)

Let us now turn to the uniqueness of the solution (28). It is immediately seen that the functions and with may also be regarded as solutions of Equation (27). Any discussion of values leads, however, to contradictions in the physical behavior of.

It is claimed that every solution is expandable into a convergent Taylor series for all; this condition is probably contained in the theory of Yang and Lee [14] stating that the equation of state of a one-phase system or a system with possible phase transition is represented by an analytic function of a complex argument Z for all Z in the corresponding region, which contains a segment of the real positive axis. As stated above, solution (28) can be expanded into a convergent Taylor series for all and meets, for the case of a complex argument Z instead of z, the condition according to Yang and Lee. One now looks for further solutions. Let a solution be assumed in the form

It follows that

Expanding into a convergent Taylor series in, one now obtains

If, all the for must be zero in order to satisfy the condition above,.

Then also holds, because the condition must be satisfied for every value z. Thus vanishes identically and the solution is unique.

6. Explicit Expression for

The expression proposed [15] [16] for the volume function is

(33)

It is symmetric in the variables and linear in both and, and at the critical point it yields v. Figure 4

shows the temperature dependence of for argon and the boundaries and,

which are set by relations (31).

Figure 4. Volume function of argon versus the temperature between and. Curve 1 represents Equation (33), curve 2 gives the lower boundary, and curve 3 the upper boundary.

Expression (33) is the only one thermodynamically possible and it alone satisfies all known thermodynamic conditions (see Appendix).

The description of the two-phase state of the saturated fluid by the expression (33) admits further formu- lations of the two-phase equilibrium.

Relations (15) and (33) yield the result of the ambitious task of representing the phase-specific internal en- ergies in terms of phase-specific volumes and vapor pressure, i.e. measurable quantities:

(34)

The positive term can be written in agreement with Equations (19), (20), and (33) as

(35)

Rearranging this to yields the following very interesting

thermodynamic equations valid for:

(36)

Equation (36) are valid for temperatures to and can serve as a criterion for calculated data of a gas, if the experimental data and are considered to be trustworthy. In turn, from Equa- tion (36) one obtains

(37)

which is in agreement with Equation (34). Figure 5 shows some energy functions of saturated argon.

As mentioned by relation (35), the term gives the weighted volume value

Figure 5. Energies of saturated argon: 1, 2, 3 u, 4, 5.

. Let us recall here the mean-value theorem of the differential calculus, which, when applied to the function, yields the result

(38)

The term can thus be replaced by the function, where the function depends only on the volume ratio or. With the definitions

(39)

it holds that

(40)

The function varies strictly monotonically from the value at to the asymptotic

value 1 for, the increase being greatest with at, and decreases mono-

tonically to 0. The physical meaning of is discussed in Ref. [16] . There the phase-specific energies and are represented as a product function, , composed of the one term, which denotes the phase, and the term, which specifies the temperature dependence. The phase-specific term is related to the local interaction potential of fluid particles in the vapor space and in the liquid. With a phase change of fluid particles, the phase-specific energy value, say, becomes in a manner that can be des- cribed simply by interchanging the phase indices. This yields the following equations:

(41)

The procedure in Ref. [16] is the exact opposite of that described here: There Equation (41) serves as starting point to derive relation (40) and find their solution (38). The energy ratio depends only on the volume ratio and with the same value z is equal for all gases, i.e. is universal:

(42)

It is found that is equal to and varies with values between 0 and as z varies from high values to 1.

The ratios of the phase-specific internal energies to the evaporation energy are likewise universal and for temperatures it holds that

(43)

Finally, the integral with the heat-capacity function [17] (see Figure 6),

(44)

yields, of course, the temperature value of the fluid internal energy,

(45)

The entropy value is defined by the integral because of. Since

one gets. From this and from Equations (1) and (4) it

follows that

(46)

According to Equations (10), (34), and (45), one has. In gen- eral, it holds that [3]

Figure 6. Heat capacity of saturated argon ac- cording to Equation (44) for.

(47)

Thermodynamic equations for of the saturated fluid are listed in Table 1.

7. Results and Discussion

In treating the thermodynamic equilibrium of a fluid mass M in a volume V, a distinction is made between an equilibrium state with a free surface area among the phase volumes, vapor and condensate, and a state without a free surface. In the case, according to Gibbs the internal energy U and entropy S of the fluid are functions with minimum equilibrium value and maximum equilibrium value. As the quantities V, U, and S are proportional to the mass M, they are absolute quantities with the known thermodynamic zeros at the critical point and at the absolute temperature zero. Equations (16) to (19) and (59) afford examples of absolute order of relations between different thermodynamic functions. Extensive quantities have the additive property, where. The intensive

Table 1. Chemical potential relations [3] .

quantities of the fluid are the temperature, pressure, and the chemical

potential, which are related to one another because of and. The thermodynamic equilibrium is described by the so-called fundamental equation.

When a free surface first transpires among the phase volumes, vapor and condensate, one has the possibility by varying T and M or V, of experimentally determing the critical point of a fluid and measuring the critical values, , and. The presence of a free surface area shows at the same time that between the volumes and, in which fluid particles are homogeneously distributed, there exists an interface phase with inhomogeneous particle distribution. Unlike in volume phases, fluid particles in the interface phase are not exposed to isotropically effective interaction potentials and therefore interface particles are endowed with a surface energy and entropy. When a free surface is increasing, the redis- tribution of the fluid particles in V proceeds in the direction of decreasing U and increasing S; in other words, in the direction of decreasing F by virtue of decreasing interface free energy. Surprisingly, its value can be macroscopically determined. With as surface tension, the effect of the interaction potential of all interface particles is measurably available. The Gibbs’ Equations (6) and (7) are enlarged by the interface terms and are given by Equation (13). The interface terms are evaluated in Figure 2 for fluid argon. The ratio of free interface energy and free volume energy yields with the assumptions, and averaged values of (see Figure 2 and Figure 8) the approximate number

. This estimate explains why the free energy at the free surface A in

relation to its value in V can be completely ignored if volumetric considerations are to the fore, as in this work.

Here it is investigated whether there is a definitely specifiable functional relation between phase-specific energies and the phase-invariant energy term, which is given by Gibbs in the energy Equation (15) for the saturated fluid. The solution , Equation (33), has been known in the literature [15] [16] for many years but has remained neglected, presumably because proof of its uniqueness was lacking. This is made up for here in Section 5 by showing that the dimensionless phase-specific temperature functions and in the ansatzes for the internal energies and have the physically relevant and unique solutions and (see Equations (24)-(28) and Figure 3). Numerical evaluation of is presented in Figure 4. The presentation of in terms of and p (see Equation (34)) allows evaluating internal energy functions as shown in Figure 5 for fluid argon. As is known, with the solutions described and proved here one can represent and calculate all thermodynamic volumetric functions as functions of and. In Table 1, for example, expressions for are listed, and in the Appendix thermodynamically derived relations are investigated for their validity by means of and verified.

Acknowledgements

The author would like to thank Max Planck Institute of Plasma Physics (IPP), Garching, for providing computing facilities. He is also grateful to A. Kechriniotis and H. Tasso for helpful discussions concerning the unique solution of the phase function introduced here to describe the fluid state, and to A. M. Nicol for the English translation.

Appendix: Test Functions for the Volume Function

The correctness of Equation (33) is now demonstrated in a few test cases. With, the volume function (33) can be written as. Since, one has

(48)

From one obtains the relations

(49)

which shows the symmetry of the volume function in respect of its variables and.

At this point it is appropriate to comment on the argument of the logarithm in expression (33). As can be seen, the relations of the last line can be transformed to the relations, which are known to describe the asymptotic behavior of in the vicinity of. This shows that the argument of the logarithm must be exactly the volume ratio and cannot be, for example, the entropy ratio. An entropy ratio as argument of the logarithm would, admittedly, yield the required symmetry property, but relations could not be numerically satisfied, since one has for.

A particularly critical test for the correctness of Equation (33) is afforded by the internal relations (16) and (34). As it holds that for, it is only the terms

(50)

that have to be investigated. It is in fact found that for and for since

According to relation (20) it is postulated that the sum is not be positive. This can be confirmed since

(51)

It should be emphasized that the energy sum, which according to Equation (34) can be written as and hence evaluated as a function of the measurable quantities and p for every gas, is a negative function of the temperature, which increases strictly monotonically as the temperature and is convex in the very immediate vicinity of the critical point (see Figure 5).

The fluid energy is not positive and given by

(52)

It is negative and greater than for since and

The difference between the energy sum and must not be negative according to Equations (16) and (52). The energy Equation (15) give

(53)

This difference is not negative if

(54)

see also Figure 7. Thermodynamically correct density data confirm the validity of condition (54). For example, the formulae for and in Ref. [4] allows one to prove the correctness of condition (54) up to the critical point. On the other hand, the relations and with are valid in the critical

region. They lead to and

. The last expression is greater than,

which means that condition (54) is satisfied and that the expression instead of confirms the thermodynamically derived result.

The next example investigated is the ratio given by Equation (42). It is found that is equal to (see Figure 3) with values between 0 and -1:

Finally, the ratio of the phase-specific internal energies to the evaporation energy is considered, for which the theory yields according to relation (21). This ratio is likewise universal and the result can be confirmed with the solution (34) since

(55)

Chemical potential relations: with the identity

as starting point and by means of the expression for the volume function according to

Figure 7. Functions and of argon for temperatures between the triple point and critical point (logarithmic representation).

Equation (33), and the two temperature derivatives and are calculated as functions of p and:

(56)

(57)

(58)

and (see Figure 8)

(59)

Figure 8. Functions, , , and of argon for temperatures between the triple point and critical point.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Gibbs, J.W. (1973) A Method of Geometrical Representation of the Thermodynamic Properties of Substances by Means of Surfaces. Transactions of the Connecticut Academy, 2, 382-404.
[2]	Callen, H.B. (1960) Thermodynamics. John Wiley & Sons, New York.
[3]	Elsner, A. (2012) Applied Thermodynamics of the Real Gas with Respect to the Thermodynamic Zeros of the Entropy and Internal Energy. Physica B: Condensed Matter, 407, 1055-1067. http://dx.doi.org/10.1016/j.physb.2011.12.118
[4]	Tegeler, C., Span, R. and Wagner, W. (1999) Thermodynamic Properties of Saturated Argon. Journal of Chemical and Physical Reference Data, 28, 779-850.
[5]	Landau, L.D., Lifshitz, E.M. and Pitaevskii, L.P. (1980) Statistical Physics: Course of Theoretical Physics. Volume 5, Pergamon Press, Oxford.
[6]	Elsner, A. (2014) Thermodynamic Fit Functions of the Two-Phase Fluid and Critical Exponents. Engineering, 6, 789- 826. http://dx.doi.org/10.4236/eng.2014.612076
[7]	Stierstadt, K. (1989) Physik der Materie. VCH Verlagsgesellschaft, Weinheim, 235.
[8]	Stansfield, D. (1958) The Surface Tensions of Liquid Argon and Nitrogen. Proceedings of the Physical Society, 72, 854-866. http://dx.doi.org/10.1088/0370-1328/72/5/321
[9]	Sprow, F.B. and Prausnitz, J.M. (1966) Surface Tensions of Simple Liquids. Transactions of the Faraday Society, 62, 1097-1104. http://dx.doi.org/10.1039/tf9666201097
[10]	Dörfler, H.D. (1994) Chapter 2: Grenzflächen und Kolloidchemie. VCH Verlagsgesellschaft, Weinheim.
[11]	Hahne, E. (1993) Technische Thermodynamik. Addison-Wesley Publishing Company, Boston, 66.
[12]	Hudson, J.B. (1996) Thermodynamics of Materials. John Wiley & Sons, New York, 22, 145, 185.
[13]	Lauth, J.G. and Kowalczyk, J. (2015) Thermodynamik. Springer Verlag, Berlin, 67, 68, 115, 135, 138-142, 199-211, 365. http://dx.doi.org/10.1007/978-3-662-46229-4
[14]	Huang, K. (1987) Statistical Mechanics. John Wiley & Sons, New York.
[15]	Elsner, A. (1987) Temperature Dependence of Absolute Fluid-State Parameters. Cryogenics, 27, 189-201. http://dx.doi.org/10.1016/0011-2275(87)90018-X
[16]	Elsner, A. (1988) Thermodynamic Representation of the State of a Saturated Fluid. Physics Letters A, 130, 225-233. http://dx.doi.org/10.1016/0375-9601(88)90598-1
[17]	Elsner, A. (1993) Specific Heats of Saturated Water Vapor and Liquid. Physical Review E, 48, 1839-1843. http://dx.doi.org/10.1103/PhysRevE.48.1839