On New Dispersive SH-Waves Propagating in Piezoelectromagnetic Plate ()
1. Introduction
There is an especial class of smart magnetoelectric materials called the piezoelectromagnetics, also known as the magnetoelectroelastics. It is well-known that these smart materials can simultaneously possess mechanical, electrical, and magnetic subsystems. As a result, an external action on the electrical subsystem can cause some changes in the magnetic subsystem (and vice versa) via the mechanical subsystem. Due to this fact, these smart materials are multi-promising for exploitation in various technical devices such as filters, sensors, actuators, delay lines, lab-on-a-chip, etc. They are also available for nondestructive testing and evaluation, ultrasonic medical imaging, active control of sound and vibration, etc. Today, sensors and actuators are the most prominent transducers used in modern technologies including aerospace industry because they can have high resolution, desirable frequency response, and generate large forces. The important property of linear coupling among mechanical, electrical, and magnetic fields can render piezoelectromagnetic (composite) materials useful in many areas of modern technology. In this endeavor, piezoelectromagnetic composites consisting of combinations of two or more different piezoelectric and piezomagnetic material phases have been designed to meet specific technical needs. Such smart materials are becoming increasingly important in diverse areas of modern technology because they can permit the tailoring of special properties, unavailable in homogeneous phases. As a result, the reader can find much review work on various smart magnetoelectric materials. For instance, some reports published in 2012 and 2013 are listed in [1] -[7] .
For many technical applications, it is very important to know the wave properties of bulk and thin-film piezoelectromagnetic materials. This study relates to theoretical investigations of shear-horizontal (SH) acoustic waves in the transversely isotropic (6 mm) piezoelectromagnetic (composite) plates. The theoretical results obtained in this work were not discovered in recent book [8] published in 2012 because they are based on the new nondispersive SH-waves discovered in recent paper [9] published in 2013. It is worth noting that it is preferable to experimentally generate such SH-waves with the noncontact method [10] -[12] called the electromagnetic acoustic transducers (EMATs). So, the following section briefly reviews the theory and the third section provides the obtained explicit forms for the new dispersive SH-waves propagating in the transversely isotropic piezoelectromagnetic plates.
2. Theory of Finding of Eigenvalues and Eigenvectors
Consider a solid medium (thin film or plate) consisting of the transversely isotropic piezoelectromagnetic (PEM) material of class 6 mm. In this configuration, it is natural to exploit the rectangular coordinate system. It is fundamental to be familiar with the propagation directions of the shear-horizontal (SH) elastic plate waves when they can be coupled with both the electrical and magnetic potentials. For the transversely isotropic material of class 6 mm, the suitable propagation direction is given in the review paper by Gulyaev [13] . In the work coordinate system, the plate SH-wave can therefore propagate along the x1-axis. This propagation direction is perpendicular to both the sixfold symmetry axis managed along the x2-axis and the normal to the PEM-material surface directed along the x3-axis. The coordinate beginning is situated at the middle of the plate, where the parameter d is reserved for the plate half-thickness. The upper and lower surfaces of the plate are then situated at x3 = +d and x3 = ?d, respectively.
This is the case of the propagation of pure SH-wave [14] [15] . To study the propagation of the SH-wave coupled with both the electrical and magnetic potentials, the quasi-static approximation [8] [9] [14] -[16] must be utilized. The concept of the quasi-static approximation is potential because the speed of the electromagnetic waves is approximately five orders larger than that of the acoustic waves. The electrostatic and magnetostatic equilibrium equations can be then written using the differential forms of the corresponding Maxwell equations, namely  and
and . The electrical displacement vector D represents Gauss’s law without free charge and currents and the second equality represents a divergence of the magnetic flux vector B. Exploiting the Maxwell equations, the governing electrostatic and magnetostatic equilibrium equations therefore read:
. The electrical displacement vector D represents Gauss’s law without free charge and currents and the second equality represents a divergence of the magnetic flux vector B. Exploiting the Maxwell equations, the governing electrostatic and magnetostatic equilibrium equations therefore read: 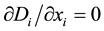 and
and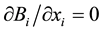 . These equations represent the partial first derivatives of the electrical displacement components Di and the magnetic displacement components Bi with respect to the real space components xi, where the index i runs from 1 to 3. Besides, the governing mechanical equilibrium equation is also written as the following partial first derivative of the stress tensor components σij with respect to xj, where the indexes i and j run from 1 to 3:
. These equations represent the partial first derivatives of the electrical displacement components Di and the magnetic displacement components Bi with respect to the real space components xi, where the index i runs from 1 to 3. Besides, the governing mechanical equilibrium equation is also written as the following partial first derivative of the stress tensor components σij with respect to xj, where the indexes i and j run from 1 to 3: . With this equation, wave motions of a PEM material in dependence on time t can be described by the following equation of motion:
. With this equation, wave motions of a PEM material in dependence on time t can be described by the following equation of motion: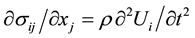 , where ρ is the mass density of the PEM bulk material. On the right-hand side of the equation there are the partial second derivatives of the mechanical displacement components Ui with respect to time t. In addition to the equation of motion written above, it is necessary to take into account the electrostatics and magnetostatics in the quasi-static approximation to form the coupled equations of motion:
, where ρ is the mass density of the PEM bulk material. On the right-hand side of the equation there are the partial second derivatives of the mechanical displacement components Ui with respect to time t. In addition to the equation of motion written above, it is necessary to take into account the electrostatics and magnetostatics in the quasi-static approximation to form the coupled equations of motion:  and
and . The coupled equations of motion are written for the case when the thermodynamic functions such as the mechanical stress tensor (σij), electrical displacements (Di) and magnetic displacements (Bi) depend on the mechanical (strain tensor ηij), electrical (field
. The coupled equations of motion are written for the case when the thermodynamic functions such as the mechanical stress tensor (σij), electrical displacements (Di) and magnetic displacements (Bi) depend on the mechanical (strain tensor ηij), electrical (field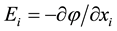 ) and magnetic (field
) and magnetic (field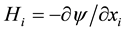 ) thermodynamic variables. Here φ and ψ are called the electrical and magnetic potentials, respectively, and they are defined by the equations written below.
) thermodynamic variables. Here φ and ψ are called the electrical and magnetic potentials, respectively, and they are defined by the equations written below.
As a result, the finally composed equations called the coupled equations of motion represent homogeneous partial differential equations of the second order. Using U4 = φ, U5 = ψ, and U2 = U called the mechanical displacement component along the x2-axis, it is natural that solutions for the coupled equations can be composed in the following plane wave forms concerning the pure SH-wave propagation:
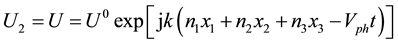 (1)
(1)
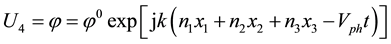 (2)
(2)
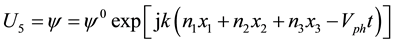 (3)
(3)
In the equations written above, U0, φ0, and ψ0 are called the initial amplitudes that should be perfectly determined as eigenvector components. j = (?1)1/2 is the imaginary unity, t and ω stand for the time and angular frequency, respectively. The phase velocity Vph is defined by the following equality: Vph = ω/k; ω = 2πν where ν is the linear frequency. The wavenumber k in the direction of wave propagation, 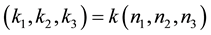 , can be naturally normalized by the wavelength λ as follows: kλ = 2π. Also, the directional cosines n1, n2, and n3 are defined as follows: n1 = 1, n2 = 0, and n3 ≡ n3.
, can be naturally normalized by the wavelength λ as follows: kλ = 2π. Also, the directional cosines n1, n2, and n3 are defined as follows: n1 = 1, n2 = 0, and n3 ≡ n3.
Next, the coupled equations of motion for the SH-wave propagation coupled with both the electrical (φ) and magnetic (ψ) potentials can be readily written in a corresponding tensor form representing the well-known modified Green-Christoffel equation. Indeed, a substitution of the solutions written in plane wave forms (1), (2), and (3) into the coupled equations of motion composed in the form of the partial differential equations can actually transform the later equations into the well-known tensor form. So, the following three homogeneous equations written in the matrix form represent the coupled equations of motion (modified Green-Christoffel equation for the case of the pure SH-wave propagation):
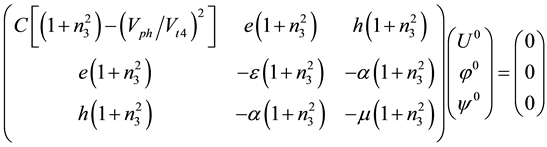 (4)
(4)
In Equation (4), n3 represents the eigenvalues and U0, φ0, and ψ0 are the eigenvector components. Also, it is essential to mention the following nonzero material parameters in expression (4): the elastic stiffness constant C, piezoelectric constant e, piezomagnetic coefficient h, dielectric permittivity coefficient ε, magnetic permeability coefficient μ, and electromagnetic constant α. They are defined as follows: C = C44 = C66, e = e16 = e34, h = h16 = h34, ε = ε11 = ε33, μ = μ11 = μ33, and α = α11 = α33 [17] [18] . Also, Vt4 stands for the speed of the shear-horizontal bulk acoustic wave (SH-BAW) uncoupled with both the electrical and magnetic potentials (pure mechanical SH-BAW):  where ρ is the mass density of the piezoelectromagnetic material.
where ρ is the mass density of the piezoelectromagnetic material.
In the case of the pure SH-wave propagation, the corresponding tensor form of the equations of motion for the piezoelectromagnetic (6 mm) medium can be written in the form of Equation (4). Solving these equations, it is possible to obtain all the eigenvalues and the corresponding eigenvectors. To discuss the problem of finding of suitable eigenvalues and the corresponding eigenvectors is the main purpose for this section. It is natural to leave all the intermediate mathematical operation and give right away the final results. So, all the six eigenvalues n3 representing the six roots of the sixth-order polynomial formed after expanding the determinant of the coefficient matrix in equation (4) are inscribed as follows:
![]() (5)
(5)
![]() (6)
(6)
In expression (6), the velocity denoted by Vtem represents the speed of the SH-BAW coupled with both the electrical and magnetic potentials. The value of Vtem is defined by the following expression:
![]() (7)
(7)
In expression (7), ![]() is called the coefficient of the magnetoelectromechanical coupling (CMEMC). This dimensionless parameter can be calculated with the following formula:
is called the coefficient of the magnetoelectromechanical coupling (CMEMC). This dimensionless parameter can be calculated with the following formula:
![]() (8)
(8)
One can find in definition (8) that the CMEMC represents the material parameter depending on the following three different coupling mechanisms discussed in paper [19] :![]() ,
, ![]() ,
,![]() . With the found eigenvalues defined by expressions (5) and (6), it is required to determine the corresponding eigenvectors in the form of (U0, φ0, ψ0) for all the eigenvalues n3. For eigenvalues (5), it is possible to have the following eigenvector components discussed in report [20] such as U0, φ0, and ψ0:
. With the found eigenvalues defined by expressions (5) and (6), it is required to determine the corresponding eigenvectors in the form of (U0, φ0, ψ0) for all the eigenvalues n3. For eigenvalues (5), it is possible to have the following eigenvector components discussed in report [20] such as U0, φ0, and ψ0:
![]() (9)
(9)
For eigenvalues (6), the corresponding eigenvector components (U0, φ0, ψ0) also mentioned in report [20] can be written as follows:
![]() (10)
(10)
because
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
In expressions (11) and (13), the coefficient of the electromechanical coupling (CEMC) is denoted by![]() . The other parameter denoted by
. The other parameter denoted by ![]() in expressions (12) and (14) couples only the terms with the electromagnetic constant α in CMEMC (6). It is central to state that the eigenvector components φ0 and ψ0 of eigenvectors (9) and (10) are naturally coupled via the corresponding CMEMC mechanism M1 mentioned above that can be expressed as follows:
in expressions (12) and (14) couples only the terms with the electromagnetic constant α in CMEMC (6). It is central to state that the eigenvector components φ0 and ψ0 of eigenvectors (9) and (10) are naturally coupled via the corresponding CMEMC mechanism M1 mentioned above that can be expressed as follows:
![]() (15)
(15)
Utilizing the found eigenvalues and eigenvectors, it is possible to compose the complete mechanical displacement UΣ, complete electrical potential φΣ, and complete magnetic potential ψΣ. These parameters can be compactly written in the plane wave form as follows:
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
Using the following equalities ![]() and
and![]() , it is possible to rewrite the complete parameters for the case of Vph < Vtem. Therefore, the parameters UΣ, φΣ, and ψΣ can be rewritten in the following convenient forms:
, it is possible to rewrite the complete parameters for the case of Vph < Vtem. Therefore, the parameters UΣ, φΣ, and ψΣ can be rewritten in the following convenient forms:
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
In these equations, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . The formulae written above are valid within the plate thickness,
. The formulae written above are valid within the plate thickness,![]() . In expressions from (19) to (21), the corresponding weight factors can be determined from equations formed with boundary conditions discussed in the following section. The main purpose of the following section is to theoretically discover several new SH-waves propagating in the transversely isotropic PEM plate. This is based on the realization of the corresponding mechanical, electrical, and magnetic boundary conditions [21] .
. In expressions from (19) to (21), the corresponding weight factors can be determined from equations formed with boundary conditions discussed in the following section. The main purpose of the following section is to theoretically discover several new SH-waves propagating in the transversely isotropic PEM plate. This is based on the realization of the corresponding mechanical, electrical, and magnetic boundary conditions [21] .
3. Boundary Conditions Leading to New Results
In this theoretical investigations there are contacts of the upper (x3 = +d) and lower (x3 = ?d) surfaces of the transversely isotropic PEM plate with the free space, also known as a vacuum. Therefore, it is also necessary to introduce the vacuum material constants and the corresponding expressions for the electrical and magnetic potentials in a vacuum. For a vacuum, the dielectric permittivity constant has the following value:
![]() where
where ![]() is the speed of light in a vacuum. For the free space, it is possible to exploit the well-known Laplace equation of type Dφf = 0 that can be written as follows:
is the speed of light in a vacuum. For the free space, it is possible to exploit the well-known Laplace equation of type Dφf = 0 that can be written as follows:![]() . The electrical potential above the upper surface (x3 = + d) of the PEM can
. The electrical potential above the upper surface (x3 = + d) of the PEM can
be written in the following plane wave form![]() , and below the
, and below the
lower surface (x3 = ?d):![]() .
.
Also, the free space magnetic permeability constant has the following value:
![]() . For the magnetic potential, Laplace’s equation of type Dψf
. For the magnetic potential, Laplace’s equation of type Dψf
= 0 can be also written in the following form:![]() . The magnetic potential in a vacuum above the
. The magnetic potential in a vacuum above the
upper surface (x3 = + d) is![]() , and below the lower surface (x3
, and below the lower surface (x3
= ?d):![]() . It is worth noting that both the electrical and magnetic potentials exponentially decrease in a vacuum when x3 > +d and x3 < ?d.
. It is worth noting that both the electrical and magnetic potentials exponentially decrease in a vacuum when x3 > +d and x3 < ?d.
Thus, it is now possible to introduce the boundary conditions at the upper and lower surfaces of the PEM plate. They are the same at both the surfaces. The mechanical boundary condition relates to the normal component of the stress tensor σ32, namely σ32 = 0. This is called the mechanical traction-free condition at the free surface. The electrical boundary conditions are the continuity of both the electrical potential φ and the normal component of the electrical displacement D3, namely φ = φf and D3 = Df, where the superscript “f” relates to the free space (vacuum). Concerning the magnetic boundary conditions, they are the continuity of both the magnetic potential ψ and the normal component of the electrical displacement B3: ψ = ψf and B3 = Bf. It is thought that it is unnecessary to give here all the complicated expressions and their transformations. Consequently, it is possible to shortly write that for these boundary conditions mentioned above, eight homogeneous equations with eight unknown parameters can be written. The eight unknown parameters are the weight factors F(1), F(2), F(3), F(4), F(5), and F(6) given in expressions from (16) to (18) and the electrical weight factor FE and the magnetic weight factor FM for a vacuum. It is a usual mathematical procedure that the weight factors FE and FM can be excluded from the further consideration and one can naturally treat six homogeneous equations with six unknown parameters F(1), F(2), F(3), F(4), F(5), and F(6). Due to the fact that in this case there are identical eigenvalues defined by expression (5), these six homogeneous equations can be rewritten as those with four unknown parameters repre- senting the weight factors F01, F02, F03, and F04. These transformations are similar to those carried out with the complete parameters in the previous section, see expressions from (19) to (21).
As a result, three homogeneous equations corresponding to the mechanical, electrical, and magnetic boundary conditions for the upper surface at x3 = +d read:
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
For the lower free surface at x3 = ?d, one can compose the following three homogeneous equations corresponding to the mechanical, electrical, and magnetic boundary conditions:
![]() (25)
(25)
![]() (26)
(26)
![]() (27)
(27)
where
![]() (28)
(28)
This set of six homogeneous equations from (22) to (27) must be resolved to get the corresponding dispersion relations. To simplify this set of homogeneous equations, it is natural to exploit the following equalities based on eigenvector components (9) and (10):
![]() (29)
(29)
![]() (30)
(30)
![]() (31)
(31)
![]() (32)
(32)
![]() (33)
(33)
![]() (34)
(34)
The employment of these equalities from (29) to (34) transforms equations from (22) to (24) written for the upper free surface of the PEM plate at x3 = +d into the following forms:
![]() (35)
(35)
![]() (36)
(36)
![]() (37)
(37)
For the lower free surface at x3 = ?d, one can also compose the following three homogeneous equations:
![]() (38)
(38)
![]() (39)
(39)
![]() (40)
(40)
These latter six equations will be used below for further proper transformations to obtain suitable solutions representing dispersion relations. This report treats two cases (i) and (ii) leading to the discovery of several new dispersive SH-waves propagating in the transversely isotropic piezoelectromagnetic plate of class 6 mm. Let’s consider the first case of them.
(i) The first case
It is obvious that to form a consistent set of equations, it is indispensable to multiply some of them by appropriate constants. Such multiplication must lead to the same dimension for all the transformed equations and change nothing because the equations are homogeneous. Indeed, one has to finally obtain the following set of three homogeneous equations: ax + by = 0, cx + dy = 0, (a + c)x + (b + d)y = 0. As soon as these three homogeneous equations will be obtained, it is obvious that it is possible to deal with the first two equations because the third equation represents a sum of the rest two equations. This is the main purpose for the further analysis. Therefore, it is possible now to write the suitable factors for this case. Analyzing the forms of Equation (37) and (40), it is natural to make a conclusion that the fitting factor for Equations (35) and (38) is ![]() and the one for Equations (36) and (39) is
and the one for Equations (36) and (39) is ![]() to form consistent equations.
to form consistent equations.
So, the final six homogeneous equations are inscribed as follows:
![]() (41)
(41)
![]() (42)
(42)
 (43)
(43)
![]() (44)
(44)
![]() (45)
(45)
![]() (46)
(46)
It is possible to say that in these six homogeneous equations written above, the CMEMC coupling mechanism such as ![]() mentioned after Equation (8) plays a major role to demonstrate that the corresponding equations are consistent. To form two different sets of three consistent equations in two unknowns, it is necessary to combine three homogeneous equations with the weight factors F01 and F03 and to separately unite the rest three equations with the weight factors F02 and F04. For this purpose, the first pair of Equations (41) and (44) must be first treated. First of all, Equation (44) must be added to Equation (41) to simplify Equation (41) and the simplified equation must be then subtracted from Equation (44). As a result, these transformations result in two simplified equations, one of them contains only the weight factors F01 and F03 and the second has only the weight factors F02 and F04. To compensate the undesirable factor of 2 in the final equations, they must be multiplied by the factor of 0.5. The same can be done for the second pair of Equations (42) and (45) and the third pair of Equations (43) and (46).
mentioned after Equation (8) plays a major role to demonstrate that the corresponding equations are consistent. To form two different sets of three consistent equations in two unknowns, it is necessary to combine three homogeneous equations with the weight factors F01 and F03 and to separately unite the rest three equations with the weight factors F02 and F04. For this purpose, the first pair of Equations (41) and (44) must be first treated. First of all, Equation (44) must be added to Equation (41) to simplify Equation (41) and the simplified equation must be then subtracted from Equation (44). As a result, these transformations result in two simplified equations, one of them contains only the weight factors F01 and F03 and the second has only the weight factors F02 and F04. To compensate the undesirable factor of 2 in the final equations, they must be multiplied by the factor of 0.5. The same can be done for the second pair of Equations (42) and (45) and the third pair of Equations (43) and (46).
Finally, the first set of three consistent equations reads:
![]() (47)
(47)
![]() (48)
(48)
![]() (49)
(49)
It is blatant that these three equations written above are consistent because the third equation of them repre- sents the sum of the rest two equations. As a result, the dispersion relation can be obtained by a successive subtraction of Equations (47) and (48) from Equation (49). The first dispersion relation for the determination of the velocity Vnew33 of the thirty third new dispersive SH-wave propagating in the transversely isotropic PEM plate is
![]() (50)
(50)
It is worth noticing that the numeration of the new SH-waves follows that used in book [8] because thirty-two new SH-waves for different boundary conditions were previously discovered in the book. This is useful because it avoids any confusion.
Concerning the second set of three consistent equations with the weight factors F02 and F04, they can be introduced in the following forms:
![]() (51)
(51)
![]() (52)
(52)
![]() (53)
(53)
With the same method, a subtraction of Equations (51) and (52) from Equation (53) can definitely lead to the second dispersion relation. This dispersion relation can actually determine the velocity Vnew34 of the thirty fourth new dispersive SH-wave. Consequently, it reads
![]() (54)
(54)
In this case, it is also likely to discuss the situation when the normalized value of the plate half-thickness kd approaches an infinity, tanh(∞) = 1 due to kd → ∞. The substitution of the value of kd → ∞ in dispersion relations (50) and (54) significantly simplify them and gives the same expression for calculation of the velocity of the nondispersive SH-wave propagating on the free surface of the PEM material. This nondispersive SH-wave was discovered in paper [9] , see formula (73) in the paper. Following the numeration of the new nondispersive SH-waves used in works [9] [17] , it is natural here to introduce this formula in the following form:
![]() (55)
(55)
where ![]() (11) and
(11) and ![]() (12) were exploited.
(12) were exploited.
(ii) The second case
Consider the second case when the other CMEMC coupling mechanism such as ![]() can play a major role to get consistent equations for determination of the propagation velocity of the plate SH-waves. In this case, it is possible to start with the treatment of six homogeneous equations from (35) to (40) anew. Equations (35) and (38) are left unchanged because they already contain the factor of
can play a major role to get consistent equations for determination of the propagation velocity of the plate SH-waves. In this case, it is possible to start with the treatment of six homogeneous equations from (35) to (40) anew. Equations (35) and (38) are left unchanged because they already contain the factor of![]() . However, the rest four equations must be properly transformed. To obtain consistent equations, it is natural that a factor of eα must be used for Equations (36) and (39) and a factor of (?hε) must be employed for equations (37) and (40). Now it is reasonable to write down consistent equations right away, because it is unnecessary here to rewrite all the mathematical procedures carried out in case (i).
. However, the rest four equations must be properly transformed. To obtain consistent equations, it is natural that a factor of eα must be used for Equations (36) and (39) and a factor of (?hε) must be employed for equations (37) and (40). Now it is reasonable to write down consistent equations right away, because it is unnecessary here to rewrite all the mathematical procedures carried out in case (i).
The first set of three consistent homogeneous equations can be unveiled in the following convenient forms:
![]() (56)
(56)
![]() (57)
(57)
![]() (58)
(58)
Next, expressions (57) and (58) must be successively subtracted from expression (56). This leads to the following intermediate dispersion relation that still contains both the weight factors F01 and F03:
![]() (59)
(59)
It is doable to exclude the weight factor F01 from the dispersion relation written above. For this aim, the dependence of F01 on F03 in expression (56) must be fittingly exploited. Finally, one can write down the following complicated dispersion relation for the determination of the velocity Vnew35 of the thirty fifth new SH-wave propagating in the transversely isotropic PEM plate:
![]() (60)
(60)
where KE and KA are defined by expressions (11) and (12), respectively.
Concerning the second set of three consistent equations with the weight factors F02 and F04, they can be introduced in the following forms:
![]() (61)
(61)
![]() (62)
(62)
![]() (63)
(63)
A consecutive subtraction of Equations (62) and (63) from Equation (61) results in the following dispersion relation containing the undesirable weight factors F02 and F04:
![]() (64)
(64)
Utilizing Equation (61), the final dispersion relation can be obtained. Therefore, one can find the following dispersion relation for the calculation of the velocity (Vnew36) values of the thirty sixth new SH-wave that can propagate in the studied plate configuration:
![]() (65)
(65)
For discovered dispersion relations (60) and (65), a substitution of tanh(∞) = 1 for an infinite value of kd → ∞ can significantly simplify them. One can check that such simplification leads to formula (79) for the nondispersive wave velocity Vnew9 obtained in paper [9] . Indeed, this simplification results in the fact that dispersion relations (60) and (65) for calculation of the dispersive SH-wave velocities are actually transformed into the same expression that determines the nondispersive SH-wave velocity. Following the numeration of the new nondispersive SH-waves utilized in paper [9] and book [17] , the formula for calculation of the velocity Vnew9 of the ninth new nondispersive shear-horizontal surface acoustic wave (SH-SAW) can be transformed into the following form:
![]() (66)
(66)
It is also worth noting that all the discovered dispersion relations are written in this report for the case of Vph < Vtem. This is the case of the fundamental modes. All the obtained dispersion relations can be readily transformed into the case of Vph > Vtem that relates to the existence of an enormous number of the higher-order modes of the dispersive SH-waves. Indeed, the fundamental modes of the dispersive SH-waves propagating in the PEM plates can be further researched for a concrete PEM material. It is expected but it is not obligatory that the obtained dispersion relations can show similar qualitative dependencies like those obtained in the investigations recently carried out in papers [22] -[24] . It is also possible to state that there are two technical regimes and they can practically supplement each other in the problem of nondestructive testing and evaluation of PEM thin films (plates). The first regime relates to the small values of the nondimensional values of kd. It is responsible for the SH-wave propagation within the whole plate that can be useful for the nondestructive detection of serious defects in the depth of the PEM material. The second regime pertains to infinite values of kd → ∞ when the value of the dispersive SH-wave velocity approaches the value of the corresponding SH-SAW. This means that in the second regime, the oscillations are localized at the free surface of the PEM material and one deals here with the corresponding SH-SAW. Therefore, it is expected that defects on the solid surface can be solidly detected and distinguished from bulk defects by the nondestructive testing technique. Thus, a plate configuration is preferable for further miniaturization of various optical and acoustical technical devices compared with bulk PEM materials. Furthermore, PEM materials can be preferable to experimentally generate PEM SH-waves with the noncontact method [10] -[12] such as the EMATs that was mentioned in the introductory section.
4. Numerical Study
Let’s graphically investigate the obtained complicated dispersion relations given by explicit forms (50), (54), (60), and (65). The piezoelectromagnetic samples are BaTiO3?CoFe2O4 and PZT-5H?Terfenol-D. The first material parameters [22] -[24] are: C = 4.4 ´ 1010 [N/m2], e = 5.8 [C/m2], h = 275.0 [T], ε = 56.4 ´ 10?10 [F/m], μ = 81.0 ´ 10?6 [N/A2], ρ = 5730 [kg/m3]. Those for the second one [22, 23, 24] are: C = 1.45 ´ 1010 [N/m2], e = 8.5 [C/m2], h = 83.8 [T], ε = 75.0 ´ 10?10 [F/m], μ = 2.61 ´ 10?6 [N/A2], ρ = 8500 [kg/m3]. The first composite is known as relatively strong piezoelectromagnetics and the second possesses significantly weaker piezoelectromagnetic properties. So, one has a contrast for comparison and better understanding of the problem of the SH- wave propagation in the PEM materials.
It is thought that the first pair of dispersion relations (50) and (54) is relatively simpler than the second pair of equations (60) and (65). Figure 1 shows the normalized velocities Vnew33/Vtem (50) and Vnew34/Vtem (54) of the fundamental modes of the dispersive SH-waves for the case of Vnew33 < Vtem and Vnew34 < Vtem. The dispersion relations are shown as functions of the normalized values of kd, where k is the wavenumber in the propagation direction and d is the plate half-thickness. It is natural to show dispersion relations for several values of the normalized material parameter α2/εµ. This parameter has a peculiarity such that α2 < εµ [1] . One can find that α2 = εµ usually occurs for practical PEM composites. However, the value of α2 < εµ cannot be too small. If the value of α2 < εµ is too small, the eighth new nondispersive SH-SAW defined by formula (55) cannot exist. As a result, the new dispersive SH-waves defined by expressions (50) and (54) cannot also exist. So, the reader can check that there are the following threshold values of α2/εµ for the studied composites: α2/εµ > (α2/εµ)th ~ 6.4 ´ 10?3 for the PZT-5H?Terfenol-D and α2/εµ > (α2/εµ)th ~ 5.0 ´ 10?7 for BaTiO3?CoFe2O4.
As soon as the value of α2/εµ > (α2/εµ)th, the new dispersive SH-waves (50) and (54) can propagate. However, when the value of α2/εµ is slightly larger than the value of (α2/εµ)th there is a relatively large “silence zone” for the Vnew33 because the value of Vnew33 is equal to zero at nonzero value of kd. Figure 1 shows that there is the same qualitative picture for both the studied composites. Indeed, the figure shows that the closer the value of α2/εµ to the value of (α2/εµ)th is situated, the larger the “silence zone” for the Vnew33 and smaller the value of the Vnew33/Vtem occur. It is thought that such technical devices as piezoelectromagnetic switches can be created based on the peculiarities discussed above. These switches will react on the SH-wave propagation: the ON-regime can be realized when the SH-waves propagate for some suitable value of α2/εµ > (α2/εµ)th and the OFF-regime is for α2/εµ < (α2/εµ)th without any SH-wave propagation. The reader can find that this is also suitable for the computer logics when the ON-regime corresponds to “1” state and the OFF-regime corresponds to “0” state, or vice versa. This can be caused and controlled, for instance, by an external magnetic field. Also, it is obvious that there is a possibility to work with very slow PEM-SH-wave speeds Vnew33 and Vnew34 for the case when the value of α2/εµ is slightly larger than the value of (α2/εµ)th. This fact and the structure geometry (thin films) can be called for further miniaturization of various technical devices such as the dispersive wave delay lines. There is also a possibility to study very slow speeds of the acoustic SH-waves coupled with both the electrical and magnetic potentials. It is hoped that some slow speeds representing only several percents from the SH-BAW speed Vtem can be readily reached in properly performed experiments.
![]() (a) (b)
(a) (b)
Figure 1. The normalized velocities Vnew33/Vtem (thick lines, formula (50)) and Vnew34/Vtem (thinner lines, formula (54)) of the fundamental modes of the dispersive SH-waves propagating in the PEM plates versus the normalized value of the half-thickness kd: (a) PZT-5H?Terfenol-D, where (1) α2/εµ = 0.006561, (2) 0.0081, (3) 0.01, (4) 0.04, (5) 0.09; (b) BaTiO3?CoFe2O4, where (1) α2/εµ = 5.329 ´ 10?7, (2) 6.4 ´ 10?7, (3) 1.0 ´ 10?6, (4) 1.0 ´ 10?4.
There is also the second figure for further discussions. The second figure studies dispersion relations (60) and (65). It was mentioned above that these dispersion relations are more complicated in comparison with the first pair of the dispersion relations graphically studied in the first figure. The normalized velocities Vnew35/Vtem (formula (60)) and Vnew36/Vtem (formula (65)) for the PZT-5H?Terfenol-D are shown in Figure 2(a) and Figure 2(b), respectively. The same velocities for the BaTiO3?CoFe2O4 are shown in Figure 2(c) and Figure 2(d), respectively. It is necessary to state right away that the qualitative picture is the same in majority for both the studied composites. However, it is preferable to discuss the PZT-5H?Terfenol-D composite because it provides definitely more informative picture due to the significantly stronger piezoelectromagnetic properties. First of all, it is crucial to introduce the peculiarity for this case shown in Figure 3. The reader can find in the third figure that for each studied sample there is one crossing point between the new SH-SAW velocity Vnew9 and the well-known
![]() (a) (b)
(a) (b)![]() (c) (d)
(c) (d)
Figure 2. The normalized velocities Vnew35/Vtem (formula (60)) and Vnew36/Vtem (formula (65)) of the fundamental modes of the dispersive SH-waves propagating in the PEM plates versus the normalized value of the half-thickness kd: (a) Vnew35 in PZT-5H?Terfenol-D, where (1) α2/εµ = 1.0 ´ 10?8, (2) 0.01, (3) 0.09, (4) 0.16, (5) 0.25, (6) 0.36, (7) 0.49, (8) 0.64, (9) 0.81, (10) 0.9801, (11) 0.998001; (b) Vnew36 in PZT-5H?Terfenol-D, where (1) α2/εµ = 1.0 ´ 10?8, (2) 0.04, (3) 0.2809, (4) 0.36, (5) 0.49, (6) 0.81, (7) 0.9801, (8) 0.998001, (9) 0,99980001; (c) Vnew35 in BaTiO3?CoFe2O4, where (1) α2/εµ = 1.0 ´ 10?8, (2) 0.01, (3) 0.04, (4) 0.09, (5) 0.1521, (6) 0.16, (7) 0.36, (8) 0.64, (9) 0.81, (10) 0.9801, (11) 0.998001; (d) Vnew36 in BaTiO3?CoFe2O4, where (1) α2/εµ = 1.0 ´ 10?8, (2) 0.1521, (3) 0.1565389225, (4) 0.16, (5) 0.36, (6) 0.64, (7) 0.81, (8) 0.9801.
![]()
Figure 3. The normalized velocities VBGM/Vtem (dotted lines) and Vnew9/Vtem (solid lines, formula (66)) of the nondispersive SH-SAWs propagating in the PEMs such as PZT-5H?Terfenol-D (black lines) and BaTiO3?CoFe2O4 (gray lines) versus the normalized parameter α2/εµ.
SH-SAW called the surface Bleustein-Gulyaev-Melkumyan (BGM) wave discovered by Melkumyan [25] , discussed in review [1] , and studied in paper [26] . The surface BGM wave propagates with the speed VBGM. The mentioned peculiarity is that there are two different behaviors in Figure 2 for the cases of Vnew9 > VBGM and Vnew9 < VBGM. Therefore there must exist the case of Vnew9 = VBGM. According to Figure 3 and the title of Figure 2, this happens at the value of α2/εµ = (α2/εµ)BGM ~ 0.2809 for PZT-5H?Terfenol-D and α2/εµ = (α2/εµ)BGM ~ 0.1565389225 for BaTiO3?CoFe2O4. With Figure 2(a) and Figure 2(b) for PZT-5H?Terfenol-D, the reader can find that the case of α2/εµ < (α2/εµ)BGM relates to the usual dispersion relations. This means that the velocity Vnew35 starts with zero value at a nonzero value of kd (Figure 2(a)) and Vnew35(kd → ∞) → Vnew9. Regarding the velocity Vnew36 shown in Figure 2(b) there is also Vnew36(kd → ∞) → Vnew9. In this study there is an interest in investigation of the fundamental modes in the case of Vph < Vtem. Therefore, Figure 2(b) and Figure 2(d) show only the case of Vnew36 < Vtem. Figure 2(a) and Figure 2(c) show that the “silence zone” can also occur. It is worth noticing that the case of α2/εµ < (α2/εµ)BGM can be commercially realizable because α2 = εµ occurs for all known PEM composites.
Let’s also discuss the case of α2/εµ > (α2/εµ)BGM. It is clearly seen in Figure 2(a) and Figure 2(b) for PZT-5H?Terfenol-D that the case of Vnew9 < VBGM for α2/εµ > (α2/εµ)BGM can provide an extra peculiarity. This peculiarity relates to the existence of the extreme points. Also, this case does not demonstrate a “silence zone” in Figure 2(a) that can be found in Figure 2(b). For the PZT-5H?Terfenol-D composite, the minimum and maximum points are clearly seen in Figure 2(a) and Figure 2(b), respectively. They can also exist in Figure 2(c) and Figure 2(d) for composite BaTiO3?CoFe2O4. However, these figures are quite unsuitable for the analysis due to the very smooth extremes. The significantly stronger piezoelectromagnetics such as PZT-5H?Terfenol-D is more preferable for the purpose of solid demonstration of the existence of the extreme points in the dispersion relations. The extreme points pertain to the phenomenon called the nondispersive Zakharenko waves [27] [28] . The nondispersive Zakharenko waves were first discovered in paper [27] when a two-layer structure was treated. Paper [28] discusses that the nondispersive Zakharenko waves can also exist in plates and quantum systems.
The existence of the nondispersive Zakharenko waves (Vph = Vg ≠ 0) follows from the following coupled behavior of the phase Vph and group Vg velocities [27] [28] :
![]() (67)
(67)
where the dependence Vph(kd) represents Vnew35(kd) or Vnew36(kd) in this case.
Formula (67) states that an increase in the phase velocity Vph(kd) results in Vph < Vg. Also, any decrease in the phase velocity Vph(kd) leads to Vph > Vg. Thus, the reader can conclude that there are two different types of the wave dispersion: Vph < Vg and Vph > Vg. It is expected that a nondispersive wave can propagate for longer distances than any (weakly) dispersive wave around. It is also necessary to mention that the nondispersive Zakharenko wave divides the corresponding mode of the dispersive SH-waves into two submodes (modes) with the different dispersions: Vph < Vg and Vph > Vg. This fact can be used because it is well-known that the Love type waves possessing Vph > Vg can demonstrate the best sensitivity.
5. Conclusion
This report has delved into the propagation problems of the shear-horizontal (SH) waves in the piezoelectromagnetic (PEM) plates. This theoretical investigation has analytically exhibited the existence of extra four new dispersive SH-waves propagating in the transversely isotropic PEM plates of class 6 mm. These discovered new SH-waves pertain to the homogeneous case when the following set of the mechanical, electrical, and magnetic boundary conditions is applied to both the upper and lower free surfaces of the PEM plate: σ32 = 0, φ = φf, D = Df, ψ = ψf, and B = Bf, where the superscript f stands for the free space, also known as a vacuum. The obtained dispersion relations for these four new dispersive SH-waves were also graphically studied. The graphical study of the obtained complicated dispersion relations has demonstrated several peculiarities that were also discussed. It is obvious that the plate SH-waves can be useful for further miniaturization of various technical devices because two-dimensional plates can be used instead of three-dimensional bulk (composite) materials. Also, the plate SH-waves can be used for nondestructive testing and evaluation of PEM thin films.
Acknowledgements
The author is thankful to the participants (Professor Dr. A.F. Sadreev, Professor Dr. V.I. Zinenko, Professor Dr. S.I. Burkov, and Dr. P.P. Turchin) of the workshop on the 8th of April, 2015 at the SB RAS L.V. Kirensky Institute of Physics, Krasnoyarsk, Siberia, Russia, for some useful notes and fruitful discussion. The author is also thankful to the referees for their valuable comments and suggestions to improve the quality of the paper for the Journal reader.