Left Chiral Solutions for the Hydrogen Atom of the Wave Equation for Electron + Neutrino

Claude Daviau¹, Jacques Bertrand²

¹Le Moulin de la Lande, Pouillé-les-Coteaux, France.
²15 Avenue Danielle Casanova, Saint-Gratien, France.

DOI: 10.4236/jmp.2015.611166                

Abstract

The resolution of our wave equation for electron + neutrino is made in the case of the H atom. From two non-classical potentials, we get chiral solutions with the same set of quantum numbers and the same energy levels as those coming from the Dirac equation for the lone electron. These chiral solutions are available for each electronic state in any atom. We discuss the implications of these new potentials.

Keywords

Hydrogen Atom, Quantum Numbers, Energy Levels, Chirality, Electron, Neutrino, Electro-Weak Gauge

1. Introduction

The resolution of the Schrödinger equation in the case of the hydrogen atom has given the reason of the quantization of the energy levels in atoms. It has also given the E = k/n² energy level of a state with principal quantum number n. For the number of orthogonal states with principal number n, the result n² states was false and the true number 2n² comes from the existence of the spin of the electron. P.A.M. Dirac found his wave equation in 1928 [1] , the solutions in the H atom case where calculated immediately by C.G. Darwin [2] . All awaited results were obtained: the true number of energy levels, all quantum numbers compatible with the spin 1/2. Only the hyperfine structure and the Lamb effect were not obtained, therefore the Dirac wave equation is until now considered as the true wave equation for any quantum object with spin 1/2.

We previously have obtained a wave equation for a pair electron + neutrino [3] and we have generalized this equation as a wave equation for all objects of the first generation, electron, neutrino, quarks u and d with three states of color each, and their antiparticles [4] . This wave equation is form invariant under the 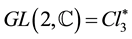group of invertible elements in the Clifford algebra of space Cl₃. It has a mass term and nevertheless it is gauge invariant under the 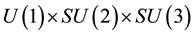gauge group of the standard model, in a way that gives automatically the insensitivity of the electron and its neutrino to strong interactions. The first consequence of this is a separation of the wave equation into a lepton part and a quark part. If the quark part is canceled, the wave is reduced to the electron + neutrino case, gauge invariant under the 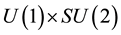group of electro-weak interactions. If the neutrino wave is canceled, the wave equation is reduced to an equation for the electron alone which has the Dirac equation as linear approximation [5] -[8] . Since the wave equation has not lost its mass term, it is easy to account for inertia and gravitation [9] .

2. Resolution in the Case of the H Atom

The wave equation for electron + neutrino reads:

(1)

where and

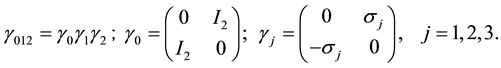(2)

The are the three Pauli matrices. We identify the Clifford algebra of space Cl₃ to the Pauli algebra considered as an algebra on the real field. We identify the space-time algebra 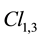to the real algebra generated by the 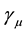and their products. In the particular case that we consider here we shall get 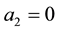and this gives

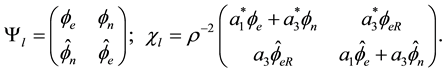(3)

Quantum mechanics uses for the electron and its neutrino three spinor waves: the left 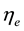and right 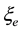waves of the electron and the left of the neutrino. The standard model has nothing to do with a right wave of the neutrino and therefore we use:

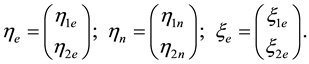(4)

The link between these chiral waves and our ones is form invariant under 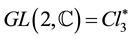by

(5)

The are the relativistic invariant densities satisfying:

(6)

where β is the Yvon-Takabayasi angle. Left and right parts of the wave satisfy:

(7)

The covariant derivative D of the electro-weak gauge reads [9] :

(8)

(9)

(10)

This covariant derivative uses four operators, , satisfying

(11)

The wave Equation (1) of the electron + neutrino is then equivalent to the system:

(12)

Using and this system is equivalent to

(13)

We suppose now that the proton of the hydrogen atom creates two potential terms:

(14)

where is the fine structure constant and we get:

(15)

A simple solution to get is:

(16)

We then have to solve the system:

(17)

And we get now

(18)

The system to be solved is then reduced to

(19)

Subtracting the last equation to the preceding, we get the equivalent system:

(20)

We shall use now the method of separation of variables in spherical coordinates. This method is usual in mathematics, but here this separation is very difficult. It is a mathematical prowess found 63 years after the Dirac equation by H. Krüger [10] . He let (with our notations):

(21)

and he got:

(22)

Now we let

(23)

This gives

(24)

(25)

which gives

(26)

This allows to separate both and from and:

(27)

3. Separating r from θ

We let now:

(28)

where a, b, c, d are functions with complex value of the real variables r and θ. We get then:

(29)

The system (27) is then equivalent to

(30)

In addition, we have:

(31)

so we get:

(32)

For the four Equations (30) there are only two angular operators, so we let:

(33)

where A, B, C and D are functions of r whilst U and V are functions of θ. The system (28) becomes:

(34)

So if a constant exists such as:

(35)

the system (34) is equivalent to the system:

(36)

which is exactly the system that we got for the lone electron from our nonlinear homogeneous wave equation (see [7] [9] (C.37)). This wave equation, which is also our wave equation for electron + neutrino where the neutrino wave is canceled, has the Dirac equation as linear approximation if and only if the Yvon-Takabayasi β angle is zero or is negligible, and we shall see later that this condition is always and everywhere satisfied. Then the radial system (34) is reduced to

(37)

We summarize now the results obtained in the study of these angular and radial systems. and being the usual angular momentum operators, the eigenvalue of is (named magnetic momentum number) and the eigenvalue of is if and only if

(38)

Next is a well-defined function, with a unique value, only if has a half-odd value. General results on angular momentum operators imply then:

(39)

To solve the angular system, if we let, with:

(40)

If we let:

(41)

The angular system (35) is then equivalent [5] to the differential equation:

(42)

The change of variable:

(43)

gives then the differential equation of the Gegenbauer’s polynomials

(44)

And we get, as only integrable solution:

(45)

with:

(46)

The factor is a factor of U and V, its phase may be absorbed by the in (23), and its amplitude may be transferred on the radial functions. We can therefore let, this gives:

(47)

Since we have the conditions (39) on and, an integer n always exists such as

(48)

and this forces the (47) series to be a finite sum, so and are integrable. And since U and V have real values, we have:

(49)

To solve the radial system we let

(50)

where F is the hypergeometric function. We get the Sommerfeld’s formula for the energy levels:

(51)

We get also:

(52)

where is, as, a complex constant. If these constants satisfy

(53)

where k is a real positive constant, the Yvon-Takabayasi β angle satisfies:

(54)

The denominator contains only sums of squares, which cannot be together null. For all bound states a solution exists such that the Yvon-Takabayasi β angle is everywhere defined. Moreover the presence of the fine structure constant, which is small, implies that the β angle is everywhere small. Next we have explained in ([7] C.4) why is exactly null, for any value of and, in the plane. Then in this plane the separation of variables (33) is exact and the system of equations (17) of the electron + neutrino is exactly solved by the linear systems of angular and radial equations (35) and (37). Since the quantification is implied by this resolution, we have the same quantification for our wave equation of electron + neutrino with the only condition (14) on the potentials created by the proton.

4. Probability and Normalization of the Wave

The wave Equation (1) has a double link with its Lagrangian density: like in the Dirac theory the wave equation may be obtained by the mathematical computation of the variation calculus, it is by this way that we have obtained our wave equation. And is also the real part of the wave equation, in the sense of Clifford algebras which always include the field on which they are built. This Lagrangian density reads (see [9] (B.71)):

(55)

Since this Lagrangian density is invariant under translations a conservative momentum-energy tensor exists. It reads

(56)

Like in the case of the electron alone (see [9] , Sec. 9.2) we get in the case of a stationary state with energy E, by the principle of equivalence between inertial and gravitational mass-energy:

(57)

With the wave Equation (1) we get

(58)

Therefore (57) is equivalent to

(59)

By letting

(60)

we define a scalar product on the quantum states and two solutions, of (1) having a different set of quantum numbers, j, , n satisfy

(61)

This last relation is not trivial and comes from the orthogonal polynomial functions used both in the angular system and in the radial system. The scalar product defined in (60) is moreover not the usual Hermitian product of quantum mechanics, but the Euclidean product that is natural in a real Clifford algebra [11] . The condition determines the value of the k constant in (53). The result is different for the electron + neutrino from the alone electron, because in the case of an alone electron we get

(62)

while in the case of electron + neutrino we get

(63)

5. Concluding Remarks

The solutions presented here are new and unexpected. We have begun the calculation with the same potential that everyone previously used. But with this potential, there are no solutions with a nonzero wave. Solutions with a nonzero neutrino wave are chiral since the neutrino has only a left wave. The wave is then made of one right wave and of two left waves. These two left waves are equal only if we consider the wave as a function of space-time in the space algebra, where we have. But if we use the correct frame, which is, for the electroweak theory, the space-time algebra, we need:

(64)

Therefore, we have and we cannot say that there is only one left wave. These waves are in two different linear spaces and do not cancel one another. The chirality is intrinsic to the electron + neutrino wave. Our solutions are then good candidates to explain why left chirality is dominant in biochemical molecules. The solutions found in 1928 from the Dirac equation had all expected properties: all necessary quantum numbers, including the spin, the true number of states, the true energy levels. Nevertheless, it is not enough to prove that the Dirac equation is the true wave equation, since we have just obtained another set of wave functions with the same quantum numbers, same number of states and same energy levels. And these new solutions have a left chirality that the solutions with the old potential and the lone electron do not have.

To get these new solutions, it is necessary to use other potential terms. This comes from the necessity to have the same term in each Equation (34). Then this term is present in all Equations (37), next this system may split into two linked systems and this allows the existence of the integrable required solutions. These conditions of integrability, coming from the equivalence principle, imply the finiteness of series and furnish the quantum number n and then the quantification of the energy levels. Our calculation proves that the potential, even if it was used with the Schrödinger equation since 1926, even if it is today the basis of all orbitals in chemistry, may not be the true potential created by the proton. From a theoretical point of view, since there are not one but two constants of structure in the gauge group of electro-weak interactions, it is not at all astonishing that two potential terms are created by the proton. We may also remark that the sum is zero. And this seems to comfort the point of view of T. Socroun that the true potentials in a unified theory including gravitation [12] must include the constant of structures. The potential terms and the covariant vectors awaited in a theory of gravitation [9] .

The solutions for the H atom where calculated from the Schrödinger equation or from the Dirac equation with a potential. This potential, in the electro-weak theory, is linked to the B and terms by the angle of Weinberg-Salam:

(65)

Here we have not changed this relation. But we do not need the A and terms, we need only and,. This is an important change which implies the novelty of our resolution in the case of the hydrogen atom.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Dirac, P.A.M. (1928) Proceedings of the Royal Society of London, 117, 610-624. http://dx.doi.org/10.1098/rspa.1928.0023
[2]	Darwin, C.G. (1928) Proceedings of the Royal Society of London, 118, 554.
[3]	Daviau, C. and Bertrand, J. (2014) Journal of Modern Physics, 5, 1001-1022. http://dx.doi.org/10.4236/jmp.2014.511102
[4]	Daviau, C. and Bertrand, J. (2014) Journal of Modern Physics, 5, 2149-2173. http://dx.doi.org/10.4236/jmp.2014.518210
[5]	Daviau, C. (1993) Equation de Dirac non linéaire. Ph.D. Thesis, Université de Nantes, Nantes.
[6]	Daviau, C. (2013) Advances in Imaging and Electron Physics, 179, 1-137. http://dx.doi.org/10.1016/B978-0-12-407700-3.00001-6
[7]	Daviau, C. and Bertrand, J. (2014) New Insights in the Standard Model of Quantum Physics in Clifford Algebra. Je Publie, Pouillé-les-Coteaux. http://hal.archives-ouvertes.fr/hal-00907848
[8]	Daviau, C. (2015) Advances in Applied Clifford Algebras, 25.
[9]	Daviau, C. and Bertrand, J. (2015) The Standard Model of Quantum Physics in Clifford Algebra. World Science Publishing.
[10]	Krüger, H. (1991) New Solutions of the Dirac Equation for Central Fields. In: Hestenes, D. and Weingartshofer, A., Eds., The Electron, Kluwer, Dordrecht. http://dx.doi.org/10.1007/978-94-011-3570-2_4
[11]	Daviau, C. (1997) Advances in Applied Clifford Algebras, 7, 175-194.
[12]	Socroun, T. (2015) Advances in Applied Clifford Algebras, 25. http://dx.doi.org/10.1007/s00006-015-0558-5