1. Introduction
Identification of X-rays and EUV fine structure lines of Lithium-like Argon is needed in laboratory and in astrophysical plasma. The X-rays emitted from highly ionized atoms are proved to be important in determining the various plasma parameters [1] [2] .
Experimental data [3] - [5] have been obtained in order to be compared with the theoretical predictions. Theoretical calculations of the energy levels, radiative rates and electron impact excitation rates for transitions in Li-like ions with 12 ≤ Z ≤ 20 and 2 ≤ n ≤ 5 were performed [6] . Electron self-energy screening approximations have been used in multi-electron atoms [7] . Relativistic configuration-interaction calculation of the energy levels of the core-excited states of lithium-like ions was presented [8] . The energies, transition probabilities and oscillator strengths for the electric dipole transitions between the levels of the ground and the low-lying excited states have been calculated using the multi-configuration Dirac-Hartree-Fock method [9] . Theoretical calculations were performed for the Kβ satellite X-rays in the active space approximation using multiconfiguration Dirac- Fock wave functions with the inclusion of the finite nuclear size effect, the Breit interaction and the quantum electrodynamic corrections [10] . The Breit-Pauli R-matrix method has been used to compute the transitions from the upper configurations (n = 4, 5) [11] . The dipole-length, dipole-velocity and dipole-acceleration absorption oscillator strengths were calculated using the energies and the multiconfiguration interaction wave functions obtained from a full core plus the correlation method, in which relativistic and mass-polarization effects on the energy, as a first-order perturbation corrections, are included [12] .
The relativistic energies, fine structures, hyperfine structures, Auger rates and widths of the core-excited states for the Li isoelectronic sequence were studied using the saddle-point variational method and the saddle-point com- plex-rotation method [13] . Electron-impact excitation for Li-like isoelectronic sequence has been obtained using the radiation and Auger damped intermediate-coupling frame transformation R-matrix approach [14] .
In the present work, fine structure energy levels, wavelengths, log gf and radiative allowed transition probabilities are presented for Ar XVI. The calculations have been performed using the Breit-Pauli (BP) approximation, for describing the relativistic interaction between electrons. That is to say, the calculations include both the relativistic Hartree-Fock (RHF) in LS coupling and relativistic correction. The interpretation of the configuration level structures are made by least-squares fit of the observed levels. The least-squares fitting procedure is used to regularize the energy levels. These adjusted fine structure energy levels are used to calculate the transition probabilities. The total number of considered Ar XVI levels is found to be 69, with 546 allowed transition rates. The configuration 1s22s of Li-like ions is taken as the ground state. The energy of the other electronic configurations nili is obtained by adjusting the scaling parameters Eav and ζi(ri) and is listed in Table 1. The calculated fine structure energy levels have been tabulated and compared with the experimental and theoretical data [4] [11] . The allowed electric dipole transition probabilities have been also compared with Ref. [11] using Breit- Pauli R-matrix (BPRM) method and no corresponding experimental data have been found in the literature.
2. Calculation Method
2.1. Atomic Structure Theory
In nonrelativistic LS coupling calculations, the normal starting point is Schrödinger’s equation where the Hamiltonian for a multi-electron system, in atomic units is given as [15]
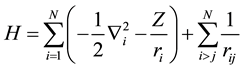 (1)
(1)
A stationary state of N-electrons is described by a wave function , where
, where  repre- sents the space and spin coordinates of the electron i.
repre- sents the space and spin coordinates of the electron i.
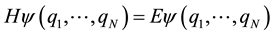
The wave function is assumed continuous with respect to the space variables and is the solution of the wave equation.
In the multiconfiguration approximation, the wave functions for a state labeled aJMJ are expanded in terms of the configuration state functions
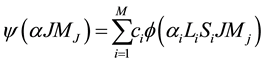 (2)
(2)
where a representing the configuration and also the set of quantum numbers both required to specify the state.
2.2. The Relativistic Effects
Breit-Pauli approximation, for describing the relativistic interaction between electrons in an approximate form is [16]
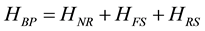 (3)
(3)
HNR is the non-relativistic multi-electron system hamiltonian. The fine-structure operator HFS is
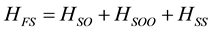 (4)
(4)
where HSO is the nuclear spin-orbit term, HSOO is the spin-other-orbit term and HSS is the spin-spin term.
The relativistic shift operator HRS commutes with L and S and can be written
![]()
Table 1. Radial function parameters for Ar XVI ion in units of 1000 cm−1.
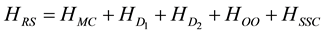 (5)
(5)
where 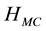 is the mass correction term,
is the mass correction term, 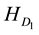 and
and  are the one and two body Darwin terms,
are the one and two body Darwin terms, 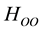 is the orbit?orbit term and
is the orbit?orbit term and 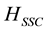 is the spin-spin contact term.
is the spin-spin contact term.
The radial wave functions have been generated using the Relativistic Hartree-Fock (RHF) method introduced, using the computer codes (Cowan ATOMIC STRUCTURE PACKAGE) [17] . The relativistic corrections included in the differential equations are derived from the Pauli-approximation to the Dirac-Hartree?Fock equations. The mass-velocity and the Darwin operators are included in the calculations. The radial parameters have been fitted in the least square optimizing program fitting the eigen-values of the hamiltonian to the available experimental energy levels. These optimized integrals have been used to compute both the wavelengths and the transition rates.
2.3. Electric Dipole Decay Rates
The strength of a line is defined as the square of the reduced dipole matrix element [18]
 (6)
(6)
where ψ and ψ' are the wave functions composed of many basis states, the sum runs over all N electrons of the atom (or ion) and ri is the radial position of the ith electron.
The transition probability is related to S according to
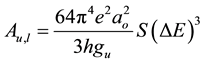 (7)
(7)
where u and l represents the upper and lower levels, respectively, gu is the statistical weight of the upper level of the transition, ao is the Bohr radius and ∆E is the wave number of the spectral line in cm−1.
The weighted oscillator strength for the transition between ψ and ψ' is defined as
![]() (8)
(8)
3. Results and Discussion
The diagonalization of the energy matrices with RHF values for the energy parameters leads to the theoretical predictions for the energy levels of the configurations. The computer code [17] is used to calculate energy levels, wavelengths, log gf and electric dipole transition probabilities. For even parity, the configurations 1s2ns, nd and ng (n = 6 - 10) have been considered while 1s2np and nf (n = 6 - 10) are considered for the odd parity configurations. They correspond to total angular momenta 1/2 ≤ J ≤ 9/2 of even and odd parities with n = 6 - 10 while orbital angular momenta 0 ≤ L ≤ 4 and spin multiplicity (2S + 1) = 2.
The mentioned configurations for the experimental energy levels taken from Ref. [4] are used in the fitting procedure for Ar XVI. For 1s2ns there is only one parameter (Eav) which is determined from the observed term 2S1/2, for 1s2nd there are two parameters (Eav, ζ2) which are determined from the observed terms 2D3/2 and 2D5/2, for 1s2ng there are two parameters (Eav, ζ2) which are determined from the observed terms 2G7/2 and 2G9/2, for 1s2np there are two parameters (Eav, ζ1) which are determined from the observed terms 2P1/2 and 2P3/2 and for 1s2nf there are two parameters (Eav, ζ2) which are determined from the observed terms 2F5/2, 2F7/2.
The energy of the other electronic configurations are obtained by adjusting the scaling parameters Eav and ζi(ri) are listed in Table 1.
A total of 69 fine structure energy levels for Ar XVI are listed in Table 2, as well as the values compiled by Ref. [4] and those calculated in Ref. [11] .
The calculated fine structure energy levels of the Ar XVI ion agree with the observed and calculated values within the range of 0.15% for most levels. However, ab initio calculations including relativistic effects in the Breit-Pauli R-matrix (BPRM) method by Nahar [11] show a good agreement with the present calculations of fine structure energy levels.
The wavelengths λ (in units of Ǻ), log gf and radiative transition probabilities for spontaneous emission (in units of 108 s−1) for 546 electric dipole allowed transitions E1 are obtained from BP calculations. Table 3 shows
![]()
Table 2. The calculated energy levels in cm−1 for Ar XVI in comparison with literatures.
the comparison of the present calculations with calculated in the literature [11] . The calculated transition probabilities in the soft X-ray region in the range 14.019 - 98.333Ǻ is within the range 0.017% - 10% accuracy those calculated in Ref. [11] using the Breit-Pauli R-matrix method. The transition probabilities in the EUV region 100.833 - 761.646 Ǻ show a very good agreement within 0.0065% - 10% with the available calculated [11] values. In the far UV 1034.869 - 1557.121 Ǻ, the calculated transition probabilities is in agreement with the calculated values [11] within the range 0.22% - 8.8% accuracy. The transition probabilities in the near infra red and mid-infra red regions 10,557.487 - 132,266.211 Ǻ show an agreement within 57% - 65% with the calculated [11] results. The calculated transition probability of the spectral line 49,449.846 Ǻ of the 1s210s2S1/2 - 1s210p2P3/2 transition shows 59% discrepancy with the calculated results [11] . Since in the present work, the COWAN code [17] , taking into account the relativistic and configuration interaction effects has been used. There is a difference in the present results using the Breit-Pauli approximation and the Breit-Pauli R-matrix (BPRM) method in the near infra red and mid infra red regions. This discrepancy may due to the close coupling (CC) approximation using R-matrix method which may not accurate in the infra red regions. The data of transition probabilities for a great number of lines for Ar XVI is not available. Therefore, there is an urgent needs to the experimental data to be compared with the theoretical results. This experimental support will show the best methods that give accurate results.
4. Conclusion
Calculations have been carried out for fine structure energy levels, wavelengths and allowed transition probabilities in lithium-like Ar XVI including the relativistic effect using the Breit-Pauli approximation. Fine structure energy levels obtained from Breit-Pauli are assessed to be more accurate by 0.15% than the observed and calculated values. The transition probabilities show a good agreement in the soft X-rays, EUV and far UV regions with almost all available calculated values. A slight discrepancy appears in the near infra red and mid infra red regions in the calculated results. No experimental data for the transition probabilities exist in literatures for comparison. However, the present results show that there is an urgent need for experimental data in order to identify the spectral lines from astrophysics and the controlled thermonuclear fusion research.