A Smoothing Neural Network Algorithm for Absolute Value Equations

Feiran Wang, Zhensheng Yu, Chang Gao

College of Science, University of Shanghai for Science and Technology, Shanghai.

DOI: 10.4236/eng.2015.79052                

Abstract

In this paper, we give a smoothing neural network algorithm for absolute value equations (AVE). By using smoothing function, we reformulate the AVE as a differentiable unconstrained optimization and we establish a steep descent method to solve it. We prove the stability and the equilibrium state of the neural network to be a solution of the AVE. The numerical tests show the efficient of the proposed algorithm.

Keywords

Absolute Value Equations, Neural Network, Smoothing Function, Linear Complementarity Problem

1. Introduction

Consider the following absolute value problem [1] -[3] :

(1)

where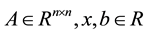, 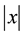is absolute value of x, it is a subclass of absolute value equations 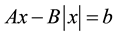which is proposed by Rohn [4] , and it is a NP-hard problem [1] .

The AVE has closed relation with some important problems, for example, the linear programming, Quadratic programming problem and the bimatrix game problem. The above problems can be transformed into the linear complementarity problem, and the linear complementarity problem can be transformed into the absolute value equations. Due to its simple and special structure and application value, the research on absolute value equation has drawn attention of many researchers. Mangasarian [5] pointed out the relationship between backpack feasibility problem and the AVE. The problem of AVE has been studied deeply by Yamashita and Fukushima [6] , and the results of the research on the problem of AVE are applied to the problem of location selection, good results are obtained. The numerical solution methods of AVE, such as Newton method, quasi-Newton method, are reachable in [7] -[12] .

In this paper, we present a smooth approximation function which is based on neural network method to solve the AVE. By using a smooth approximation function of, we turn it into a differentiable unconstrained optimization problem. Furthermore, we obtain the approximate solution of the original problem based on our established unconstrained optimization problem and the neural network model. Compared with the Newton method, the neural network model needs less requirement for the hardware of compute and the iterative process is real-time.

2. The Smoothing Reformulating of AVE

The absolute value Equation (1) is equivalent to the nonlinear equations:

(2)

where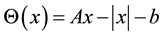. Since it is a non smooth function, we construct a smooth function to approximate it.

Definition 1.1 Smoothing approximation function, given a function, smoothing function is called smoothing approximation function, if for any, there exists so that

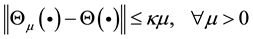
where 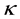is not dependent on the x.

In this paper, we use the aggregate function [13] to give a smooth approximation of the absolute value equation:

Let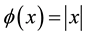, so every component of the absolute value function can be recorded as

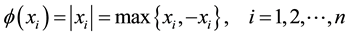
For any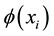, the definition of smoothing function is as follows

So the function of absolute value is obtained as follows

Thus the absolute value equation is transformed into the following smooth equations

(3)

where

We define the function as follows

where is the smoothing approximation of, is said as the energy function

of the neural network. Thus, the approximate solution of the absolute value equation is transformed to the global optimal solution of the optimization problem

3. Neural Network Model for Absolute Value Equation

Consider the following unconstrained optimization problem

(4)

the gradient can be calculated by the following formula:

where

now, we can give a neural network model for solving the absolute value equation, which is based on the steepest descent neural network model for (4).

(5)

where is a parameter represents that one can use a larger step size in the simulation, specific details can be referred to [14] -[16] . To simplify our analysis, we let throughout this paper. A block diagram (Figure 1) of the neural network is shown as follows.

4. Analysis of Stability and Existence

Next, we recall some materials about first order differential equations (ODE) [17] :

(6)

where is a mapping. We also introduce three kinds of stability that will be discussed later.

Definition 3.1 A point is called an equilibrium point or a steady state of the dynamic system (6)

if If the reisaneighborhood of such that a,

then is called an isolated equilibrium point.

Lemma 3.1 Assume that is a continuous mapping. Then, for any and, there exists a local solution for (6) with for some. If, in addition, H is locally Lipschitz continuous at, then the solution is unique.

Definition 3.2 (Asymptotic stability). An isolated equilibrium point is said to be asymptotically stable if

in addition to being Lyapunov stable, it has the property that as for all

Definition 3.3 (Lyapunov stability). Stability in the sense of Lyapunov Let be a solution for (6). An isolated equilibrium point is Lyapunov stable if for any and any there exists a

such that for all and

Definition 3.4 (Lyapunov function). Let be an open neighborhood of. A continuously differentiable function is said to be a Lyapunov function at the state over the set for Equation (6) if

Figure 1. The block diagram of neural network (5).

Lemma 3.2 a) An isolated equilibrium point is Lyapunov stable if there exists a Lyapunov function over some neighborhood of

b) An isolated equilibrium point is asymptotically stable if there is a Lyapunov function over some

neighborhood of such that for all

Lemma 3.3 [11] For any, , if then.

Theorem 3.1 is Lyapunov function over some neighborhood of

Proof. Let be the solution of the absolute value equation.

1) The function is obtained by our smooth approximation. So is continuous with respect to

. Obviously have continuous partial derivatives at all components of the.

2) Since, then

3) If then is always holds

So, by the Definition 3.4 we know that is Lyapunov function over some neighborhood of

Theorem 3.2 Each solution of the absolute value equation is the equilibrium point of the neural network (5).

Conversely, if, the equilibrium point of the neural network (5) is the solution of the absolute value equation.

Proof. Assume that is the solution of the absolute value equation, since, for any

we have if and only if is the solution of the absolute value equation.

Obviously, we got, so is the equilibrium point of the neural network (5). On the other

hand if and, then we get. So, the equilibrium point of the neural network (5) is the solution of the absolute value equation.

Next, we can prove that is not only Lyapunov stable and asymptotically stable.

Theorem 3.3. Let the be the isolated equilibrium of the neural network. is the Lyapunov stability and asymptotic stability for neural networks.

Proof. Since is the isolated equilibrium of the neural network, the solution of the absolute value eq-

uation is known by the Theorem 3.2. Therefore,. In addition, Since x is the isolated equilibrium

point, so and are hold over the neighborhood of. By

Theorem 3.1 we know that is Lyapunov function over some neighborhood of, so by Lemma 3.2 the isolated equilibrium is Lyapunov stable. Because is isolated, it is not difficult to compute:

Consequently, we have. By Lemma 3.2, is asymptotic stability.

5. Numerical Experiment

In this section we give some smooth of numerical tests of neural network algorithm, due to the complementarity problem can be transformed to absolute value equations, we consider the linear complementarity problem which is equivalent to the absolute value equations as test cases.

For a given matrix and vector, The linear complementarity problem is to find a vector to satisfy.

From the Theorem 2 in the literature [11] , if 1 is not the eigenvalues of the matrix, then is equivalent to the following absolute value equation:

where and is the solution of the absolute value equation.

Example 1 [11] . Consider the following linear complementary problem:

Since1 is not included in the eigenvalues of, then the linear complementary problem can be transformed into the following absolute value equation and they are equivalent:

where

We can find that is a solution of the absolute equation.

By using the neural network model, the initial point is generated by x0 = rand (n,1), and the program is performed under the environment of MATLAB7.11.0. The following two figures (Figure 2 and Figure 3) describe how the approximate solution of example 1 and the energy function varies with time.

Figure 2. Transient behavior of x(t) of example 1.

Figure 3. Transient behavior of energy function of example 1.

Since, then we can capture the solution of the linear complementary problem, the solution is.

Example 2 [11] . Consider the following linear complementary problem:

Through calculation, we can get one eigenvalue of is 1. By literature [11] , we can find that if 1 is the eigenvalue of matrix, then the and of the linear complementary problem need to be multiplied by a positive constant and makes 1 not the eigenvalue of (and the solution of the linear complementary pro- blem keeps invariant). Then we can transform linear complementary problem into absolute value equation by applied Theorem 2 and Theorem 3 in literature [11] .

Set, then we can find that 1 is not included in the eigenvalues of. And and have the common optimal solution, while z can be transformed into the absolute value equation by applying the Theorem 2. Then, we have

And the absolute value equation is, where:

Thus, we can get one solution of the absolute value equation whcih is, then the following two figures (Figure 4 and Figure 5) describe how the approximate solution of example 2 and the energy function varies with time

Since, then we can capture the solution of the linear complementary problem LCP(M,q), the solution is.

Example 3. Consider the following linear complementary problem:

Figure 4. Transient behavior of x(t) of example 2.

Figure 5. Transient behavior of energy function of example 2.

Through calculation we can get one eigenvalue of is 1. And the same as example 2, set, then, we can find that:

And the absolute value equation is:, where:

Thus, we can get the solution of the absolute value equation which is, then the following two figures (Figure 6 and Figure 7) describe how the approximate solution of example 3 and the energy function varies with time

Since, then we can capture the solution of the linear complementary problem LCP(M,q), the solution is z^* = (2.5 2.5 0 2.5).

6. Conclusion

This paper adopted the aggregate function method to tackle the absolute value equation with smooth processing, and then turned the absolute value equation into a differentiable unconstrained optimization problem. In order to obtain the approximate solution of the original problem we use the proposed neural network model to solve the

Figure 6. Transient behavior of x(t) of example 3.

Figure 7. Transient behavior of energy function of example 3.

unconstrained optimization problem. At the same time, we propose one neural network which is based on different energy function. Through the transformation between linear complementary problem and absolute value equation, it can be used to solve the linear complementary problem, too. For the traditional energy function based on the NCP function, we can avoid a lot of matrix calculation. Numerical examples show that the algorithm is very effective for solving this kind of absolute value equation, and the accuracy of solution can be controlled by the parameters completely. In view of the fact that it is relatively difficult to solve the absolute value equation, the proposed method in this paper can be used to solve the absolute value problem effectively.

Acknowledgements

This work is supported by National Natural Science Foundation of China (No.11171221) and Innovation Program of Shanghai Municipal Education Commission (No.14YZ094).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Mangasarian, O.L. and Meyer, R.R. (2006) Absolute Value Equations. Linear Algebra and Its Applications, 419, 359-367. http://dx.doi.org/10.1016/j.laa.2006.05.004
[2]	Rohn, J. (2004) A Theorem of the Alternatives for the Equation Ax + B|x| = b. Linear and Multilinear Algebra, 52, 421-426. http://dx.doi.org/10.1080/0308108042000220686
[3]	Han, J.Y., Xiu, N.H. and Qi, H.D. (2006) Nonlinear Complementary Theory and Algorithm. Shanghai Science and Technology Press, Shanghai.
[4]	Rohn, J.R. (1989) Systems of Linear Interval Equations. Linear Algebra and Its Applications, 126, 39-78. http://dx.doi.org/10.1016/0024-3795(89)90004-9
[5]	Mangasarian, O.L. (2009) Knapsack Feasibility as an Absolute Value Equation Solvable by Successive Linear Programming. Optimization Letter, 3, 161-170. http://dx.doi.org/10.1007/s11590-008-0102-9
[6]	Yamashita, S. and Fukushima, M. (2001) A Branch-and-Bound Method for Absolute Value Program and Its Application to Facility Location Problems. Kyoto University, Kyoto.
[7]	Mangasarian, O.L. (2013) Absolute Value Equation Solution via Dual Complementarity. Optimization Letters, 7, 625-630. http://dx.doi.org/10.1007/s11590-012-0469-5
[8]	Mangasarian, O.L. (2009) A Generalized Newton Method for Absolute Value Equations. Optimization Letters, 3, 101-108. http://dx.doi.org/10.1007/s11590-008-0094-5
[9]	Caccetta, L., Qu, B. and Zhou, G.L. (2011) A Globally and Quadratically Convergent Method for Absolute Value Equations. Computational Optimization and Applications, 48, 45-58. http://dx.doi.org/10.1007/s10589-009-9242-9
[10]	Rohn, J. (2009) An Algorithm for Solving the Absolute Value Equation. Electronic Journal of Linear Algebra, 18, 589-599.
[11]	Yong, L.Q. and Tuo, S.H. (2012) Quasi-Newton Method to Absolute Value Equations Based on Aggregate Function. Journal of System science and Mathematics, 32, 1427-1436.
[12]	Yong, L.Q., Liu, S.Y. and Tuo, S.H. (2014) Transformation of the Linear Complementarity Problem and the Absolute Value Equation. Journal of Jilin University (Science Edition), 4, 638-686
[13]	Li, X.S. (1991) The Aggregation Function Method for Solving the Problem of Nonlinear Mini-Max Problem. Computational Structural Mechanics and Its Application, 8, 85-92.
[14]	Chen, J.-S., Ko, C.-H. and Pan, S.H. (2010) A Neural Network Based on the Generalized Fischer-Burmeister Function for Nonlinear Complementarity Problems. Information Sciences, 180, 697-711. http://dx.doi.org/10.1016/j.ins.2009.11.014
[15]	Ma, H.Q. and Huang, N.-J. (20145) Neural Network Smoothing Approximation Method for Stochastic Variational Inequality Problems. Journal of Industrial and Management Optimization, 7, 645-660.
[16]	Liao, L.Z., Qi, H.D. and Qi, L.Q. (2001) Solving Nonlinear Complementarity Problems with Neural Networks: A Reformulation Method Approach. Journal of Computational and Applied Mathematics, 131, 343-359. http://dx.doi.org/10.1016/S0377-0427(00)00262-4
[17]	Miller, R.K. and Michel, A.N. (1982) Ordinary Differential Equations. Academic Press, Waltham.