A Series Approach to Perturbed Stochastic Volterra Equations of Convolution Type

Anna Karczewska^*, Bartosz Bandrowski

Faculty of Mathematics, Computer Science and Econometrics, University of Zielona Góra, Zielona Góra, Poland.

DOI: 10.4236/apm.2015.511060                

Abstract

In the paper, perturbed stochastic Volterra Equations with noise terms driven by series of independent scalar Wiener processes are considered. In the study, the resolvent approach to the equations under consideration is used. Sufficient conditions for the existence of strong solution to the class of perturbed stochastic Volterra Equations of convolution type are given. Regularity of stochastic convolution is supplied, as well.

Keywords

Stochastic Linear Volterra Equation, Perturbed Equation, Strong Solution, Resolvent, Mild Solution, Stochastic Convolution, Series Approach

1. Introduction

Let 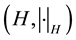be a seperable Hilbert space and let 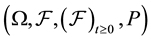denote a probability space. We consider perturbed stochastic Volterra Equations in H of the form

(1)

where 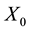is an H-valued 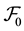-measurable random variable, kernels a, k, b are real valued and locally inte- grable functions defined on 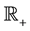and A is a closed unbounded linear operator in H with a dense domain.

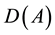The domain 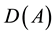is equipped with the graph norm of A, i.e..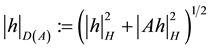

In our work, the Equation (1) is driven by series of scalar Wiener processes; and 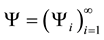are appropriate processes defined below.

The goal of this paper is to formulate sufficient conditions for the existence and regularity of strong solutions to the perturbed Volterra Equation driven by series of scalar Wiener processes. Previously, in [1] - [4] , the stochastic integral for Hilbert-Schmidt operator-valued integrands and Wiener processes with values in Hilbert space has been constructed. Moreover, the particular series expansion of the Wiener process with respect to the eigenvectors of its covariance operator has been used. The stochastic integral used in this paper, originally introduced in [5] , bases on the construction directly in terms of the sequence of independent scalar processes. In consequence, the stochastic integral is independent of any covariance operator usually connected with a noise process.

In the paper, we use the resolvent approach to the Equation (1). This means that a deterministic counterpart of the Equation (1), that is, the Equation

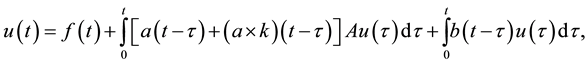(2)

admits a resolvent family. In (2), the operator A and the kernel functions are the same as previously in (1) and f is a H-valued function.

By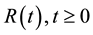, we shall denote the family of resolvent operators corresponding to the Volterra Equation (2), which is defined as follows.

Definition 1 A family of bounded linear operators in H is called resolvent for (2), if the following conditions are satisfied:

1) 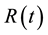is strongly continuous on and;

2) commutes with the operator A, that is, and for all ,;

3) the following resolvent equation holds

(3)

for all.

In this paper, the following result concerning convergence of resolvents for the Equation (1) will play the key role.

As in [6] , we shall assume the following hypotheses:

The solution of the Equation

is nonnegative, nonincreasing and convex.

The solution of the Equation is differentiable.

Theorem 1 ( [6] , Th.~3.5) Assume that A is the generator of bounded analytic semigroup of H. Suppose that the hypotheses and are satisfied. Then the Equation (2) admits a resolvent. Addi- tionally, there exists bounded operators and corresponding resolvent families satisfying for all, such that

(4)

for all. Moreover, the convergence (4) is uniform in t on every compact subset of.

Below we give an example illustrating conditions and.

Example 1 Consider in the Equation (1) the following kernel functions

Then the functions

fulfil conditions and.

The paper is organized as follows. Section 2 constains the construction of the stochastic integral due to O. van Gaans [5] . In Section 3, we compare mild and weak solutions and then we provide sufficient conditions for stochastic convolution to be a strong solution to the Equation (1). Section 4 gives regularity of stochastic con- volution arising in perturbed Volterra Equation while in Section 5 we derive the analogue of Itô formula to the perturbed Volterra Equation.

2. The Stochastic Integral

In this section we recall the construction of the stochastic integral due to O. van Gaans [5] .

Definition 2 A function is called piecewise uniformly continuous (PUC) if there are such that f is uniformly continuous on for each.

Definition 3 A function is called piecewise uniformly continuous (PUC), if is uniformly continuous for all.

Theorem 2 ( [5] ) Assume that is a series of independent standard scalar Wiener processes with res-

pect to the filtration in. Let be a series of piecewise uniformly continuous functions (PUC)

acting from into, adapted with respect to the filtration. Then the following results hold.

1) For any, the integral is well-defined as the limit of Riemann sums of the form

where.

2) For each, the Itô isometry holds

3) For any, such that we have

Definition 4 By we shall denote the space of series of piecewise uni- formly continuous functions (PUC) acting from into, adapted with respect to the filtration, such that

Theorem 3 ( [5] ) Assume that is a series of independent standard scalar Wiener processes with respect to the filtration in. Let. Then the integral

exists in and

3. The Main Results

We begin this section with definitions of solutions to the Equation (1).

Definition 5 An h-valued predictable process, is said to be a strong solution to (1), if has a version such that for almost all; for any

(5)

(6)

and for any the Equation (1) holds P − a.s.

Let denote the adjoint of A with a dense domain and the graph norm.

Definition 6 An H-valued predictable process, is said to be a weak solution to (1), if

and if for all and all the following equation holds

As we have already written, in the paper we assume that (2) admits a resolvent family,. So, we can introduce the following idea.

Definition 7 An H-valued predictable process, is said to be a mild solution to the pertur- bed stochastic Volterra Equation (1), if

and, for all,

(7)

where is the resolvent for the deterministic perturbed Volterra Equation (2).

We introduce the stochastic convolution

(8)

where and the resolvent operators, are the same as above.

Let us formulate some auxiliary results concerning the convolution.

Proposition 4 For arbitrary process, the process, , given by (8) has a predictable version.

Proposition 5 Assume that. Then the process, , defined by (8) has square integrable trajectories.

For the idea of proofs of Propositions 4 and 5, we refer to [2] or [3] .

In some cases, weak solutions of Equation (1) coincides with mild solutions of (1), see e.g. [2] or [3] . In con- sequence, having results for the convolution (8) we obtain results for weak solutions.

Proposition 6 Assume that. Then the stochastic convolution, , is a weak solution to the Equation (1).

Hence, we are able to conclude the following result.

Corollary 1 Let A be a linear bounded operator in H. If then

(9)

The formula (9) says that the convolution is a strong solution to (1) if the operator A is bounded.

Here we provide sufficient conditions under which the stochastic convolution, , defined by (8) is a strong solution to the Equation (1).

Lemma 1 Assume that and. Then

(10)

and

Proof Because is a Hilbert space, then the integral

exists in by Theorem 3.

Denote by division of the interval, that,

. From the definition of the integral and closedness of the operator A we have

□

Theorem 7 Let A be a closed linear unbounded operator with the dense domain equipped with the

graph norm. Suppose that assumptions of Theorem 1 hold. If and

, then the stochastic convolution is a strong solution to the perturbed sto- chastic Volterra Equation (1).

Proof Since closed unbounded linear operator A becomes bounded in, we have

Then from the properties of stochastic convolution we obtain integrability of

and. Therefore, conditions (5) and (6) from the definition of strong solution to Equation (1) hold.

It remains to show that the Equation (1) holds P − a.s., i.e.

(11)

Because the formula (9) holds for any bounded operator, then it holds for the Yosida approximation of the operator A, too. Then we have

where

and

To prove that (11) holds, we need to show the following convergences

(12)

and

(13)

By assumption. Because the operators are

deterministic and bounded for any, , then belong to, too. Hence, the difference

(14)

belongs to for every and. This means that

(15)

From the definition of stochastic integral (Theorem 3), for, we have

By Theorem 1, the convergence of the resolvent families is uniform with respect to t on every closed intervals, particularly on. Then we have

(16)

Summing up the above considerations, we obtain

as. Then, by the dominated convergence theorem the convergence (12) holds.

From the fact that and we have

. Then, by Lemma 1,.

For any, , we can write

Then

To prove that the convergence (13) holds, we need to show that

(17)

and

(18)

We shall study the term first. Because the operator A generates a semigroup, we can use the following property of the Yosida approximation

(19)

where for any,.

Moreover

(20)

For any big enough n and any, we have.

Next, by Lemma 1 and closedness of the operator A

Analogously, we have

Using (19), we receive

From assumption, so the term may be treated like the difference defined by (14).

Then, using (19) and (12), we obtain (17).

For the term we can repeat the proof of the convergence (12).

By assumption. Because and, are bounded, so

.

Analogously,.

Since, this term can be treated like the difference de- fined by (14). Hence, for any, we may write

Using the convergence (20), we have

Therefore the convergence (18) holds. □

4. Continuity of Trajectories

In this section, we give sufficient conditions for the continuity of trajectories of the stochastic convolution when the kernel function. Thus, we study the stochastic convolution corresponding to the equation

(21)

where.

Theorem 8 Let the operator A be the generator of strongly continuous bounded analytic semigroup,

. Assume that the functions, are the skalar kernel functions and con-

dition holds. If, then the following formula holds

(22)

where, is a constant and

like in Equation (1).

Proof Since formula (9) holds for any bounded operator, then it holds for the Yosida approximation of operator A as well, that is

(23)

where

Denoting

(24)

and using the Leibniz rule twice we obtain

(25)

From (23) and (24), we can write

If, then from (25) we have

and next

For simplicity, we introduce the following term

Then

Since, we can write

From (23) and (24) we obtain

where.

Then

Basing on Theorem 1, properties of Yosida approximation of the operator A, and dominated convergence theorem, we have

and

Since the operator A is closed, we can conclude that

Hence, passing to the limit with, we obtain

where

□

Lemma 2 Let the assumptions of Theorem 8 hold and. Then for,

(26)

where

(27)

and

Moreover, , P − a.s. and

(28)

Proof The formula (26) results from (22) and the definition (27) of the process. Moreover, from properties of convolution, P − a.s.

Using the Leibniz rule and property of semigroup we obtain

where. □

To conclude continuity of trajectories of stochastic convolution, we use regularity of solutions for the non- homogeneous Cauchy problem [7] to the formula (26).

Theorem 9 Suppose that the assumptions of Theorem 8 hold. If both processes Y and,

, have continuous trajectories in the space, then the stochastic convolution,

, has continuous trajectories in.

In the previous theorem, the space, , is defined as follows. For any, we set

We denote by the Banach space of all such that, endowed with the norm

. By the interpolation theory, is an invariant space of, , and the restriction of to generates a -semigroup in.

5. Analogue of the Itô Formula

In this section, we derive the analogue of the Itô formula to the perturbed Volterra Equation (1).

Proposition 10 Let the process X be a strong solution to the Equation (1) and. Suppose that the function and its partial derivatives, , are uniformly continu- ous on. Then, for any,

The following proposition is an example of application of the above analogue of the It formula.

Proposition 11 Let the operator A be the generator of bounded analytic semigroup in H. Suppose that , the conditions and hold and.

Assume that the function satisfies the following conditions:

1) function v and its partial derivatives, are uniformly continuous on bounded subsets of H,

2) for any and the constant

3) for any and the constant

Then the stochastic convolution satisfies the following inequality

The idea of the proof bases on Ichikawa’s scheme, see ( [8] , Theorem 3.1), and on Theorem 1 and Proposition 10. It seems to be a good starting point in the study of stability of mild solution to perturbed Volterra Equation (1).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Da Prato, G. and Zabczyk, J. (1992) Stochastic Equations in Infinite Dimensions. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511666223
[2]	Karczewska, A. (2007) Properties of Convolutions Arising in Stochastic Volterra Equations. International Journal of Contemporary Mathematical Sciences, 2, 1037-1051.
[3]	Karczewska, A. (2007) Convolution Type Stochastic Volterra Equations. Lecture Notes in Nonlinear Analysis. Juliusz Schauder Center for Nonlinear Studies. 10. Toruń.
[4]	Karczewska, A. and Lizama, C. (2009) Strong Solutions to Stochastic Volterra Equations. Journal of Mathematical Analysis and Applications, 349, 301-310. http://dx.doi.org/10.1016/j.jmaa.2008.09.005
[5]	van Gaans, O. (2005) A Series Approach to Stochastic Differential Equations with Infinite Dimensional Noise. Integral Equations and Operator Theory, 51, 435-458. http://dx.doi.org/10.1007/s00020-003-1258-4
[6]	Karczewska, A. and Lizama, C. (2014) Stochastic Volterra Equations under Perturbations. Electronic Communications in Probability, 19, 1-14. http://dx.doi.org/10.1214/ECP.v19-3365
[7]	Da Prato, G. and Grisvard, P. (1979) Equations d’volution abstraites non linaires de type parabolique. Annali di Matematica Pura ed Applicata, 120, 329-396. http://dx.doi.org/10.1007/BF02411952
[8]	Ichikawa, A. (1982) Stability of Semilinear Stochastic Evolution Equations. Journal of Mathematical Analysis and Applications, 90, 12-44. http://dx.doi.org/10.1016/0022-247X(82)90041-5