An Accurate Numerical Integrator for the Solution of Black Scholes Financial Model Equation ()
1. Introduction
Financial derivative, in particular options, became very popular financial contracts in the last few decades. Options can be used to hedge assets and portfolios in order to control the risk due to movements in the share price. A European call (put) option provides the right share price to buy or sell a fixed number of assets at the fixed exercised price E, at the expiry time t0 [1] . In the early 1970’s Fisher Black and Myron Scholes made a major breakthrough by deriving a partial differential equation that must be satisfied by the price of any derivative security dependent on a non-dividend-paying stock [2] . According to [3] their work had a huge impact on how options were viewed in the financial world. In an idealized financial market, the price of a European option can be obtained as the solution of the Black-Scholes equation [4] [5] . However, the Black Scholes equation has been derived under quite restrictive assumptions such as frictionless, liquid and complete market. In recent years nonlinear Black Scholes equations have been derived in order to model transaction costs arising in the hedging of portfolios [1] [6] [7] and feedback effects due to large traders [8] - [13] .
In seeking the solution of the Black Scholes equation, emphasis is always laid on derivation of formula or equation for the price of the option of interest and computation of the price of the option. This calls for the usage of numerical methods because explicit theoretical solutions for the price of the option do not exist. From a binomial model, [6] derived an option price that takes into account transaction costs which approximates a Black Scholes price but with modified volatility. [14] [15] computed the option price of the Black Scholes equation as the solution of a nonlinear quasi-variational inequality. This approach has the disadvantage that the option price depends on the choice of the utility function. Seeking the analytical solution of the Black-Scholes equation, [16] used the Adomain decomposition method. Adomain decomposition can provide analytical approximations to a wide class of linear and nonlinear equations without perturbation, closure approximations or discretization. Solution for the Black-Scholes equation as a semigroup on spaces of continuous functions on (0, ∞) is presented in [17] .
In the mathematical literature, only a few results can be found on the numerical discretization of Black Scholes equations. The numerical approaches vary from binomial approximations for American options in stochastic framework [18] , Monte-Carlo methods [19] , finite element discretization [20] , and finite difference approximations [1] . The numerical discretization of the Black Scholes equations with nonlinear volatilities has been performed using explicit finite difference schemes [21] [22] . Explicit numerical schemes have the disadvantage that restrictive conditions on the discretization parameters, time and space steps, are needed to obtain stable, convergent schemes [23] . Moreover the convergence order is the only one in time.
The Method of Lines (MOL) is a general procedure for the solution of time-dependent partial differential equations (PDEs) [24] . The basic idea of the MOL is to replace the spatial (boundary value) derivatives in the PDEs with algebraic approximations [25] . Ones this is done, the spatial derivatives are no longer stated explicitly in terms of the spatial dependent variables. Thus, only the initial value variable, typically time in a physical problem, remains, which results in a system of ODEs that approximates the original PDE. An accurate integration algorithm for initial value ODEs to compute an approximate numerical solution to the PDE can then be used for the numerical integration. One of the salient features of the MOL is the use of existing, and generally well established, numerical methods for ODEs [26] .
This paper is organized thus: In Section 2 we transform the black Scholes equation into a heat equation by change in variables. In Section 3 we introduce an L-stable trapezoidal like integrator for the numerical integration of the transformed Black Scholes equation. Section 4 is devoted to the numerical test of the method on the transformed Black Scholes equation. Section 5 explains the computation of the errors and relative errors of the method while results are discussed in Section 6.
2. Transforming the Black Scholes Equation into a Parabolic Heat Equation
Given the Black Scholes equation:
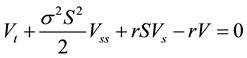 (1)
(1)
Subject to:
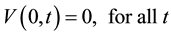 (2a)
(2a)
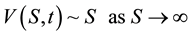 (2b)
(2b)
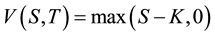 (2c)
(2c)
where:
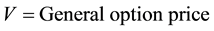 (3a)
(3a)
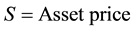 (3b)
(3b)
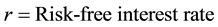 (3c)
(3c)
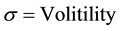 (3d)
(3d)
Following [27] to transform the diffusion-advection-reaction Equation (1) into a parabolic heat PDE, we make the following change of variables:
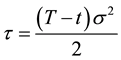 (4a)
(4a)
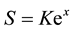 (4b)
(4b)
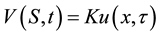 (4c)
(4c)
By taking appropriate partial derivatives of  in Equation (4c) and substituting in Equation (1) yields
in Equation (4c) and substituting in Equation (1) yields
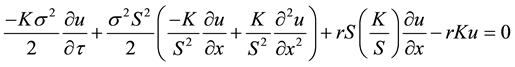 (5)
(5)
Substituting 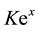 for
for  in Equation (5) and dividing by
in Equation (5) and dividing by 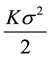 yields
yields
![]() (6)
(6)
Defining
![]() (7)
(7)
And substituting for k in Equation (6) we obtain
![]() (8)
(8)
By defining
![]() (9)
(9)
Then, the partial derivatives of ![]() are thus obtained:
are thus obtained:
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
Making ![]() and
and ![]() the subjects of Equations (10), (11) and (12) respectively we obtain:
the subjects of Equations (10), (11) and (12) respectively we obtain:
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
Substituting Equations (13), (14) and (15) into Equation (8) we obtain
![]() (16)
(16)
By letting the coefficients of ![]() and
and ![]() in Equation (16) vanish identically
in Equation (16) vanish identically
Under the condition that
![]() (17)
(17)
and
![]() (18)
(18)
the Black Scholes equation given in Equation (1) is transformed into the parabolic heat equation PDE
![]() (19)
(19)
Subject to
![]() (20a)
(20a)
![]() (20b)
(20b)
According to [28] European Call option as the solution to the Black Scholes equation on ![]() can be approximated by
can be approximated by
![]() (21)
(21)
Equating both hand sides of Equation (21) yields
![]() (22)
(22)
Substituting for S from Equation (4) in Equation (22) gives
![]() (23)
(23)
Substituting ![]() for
for ![]() in Equation (23) from Equation (3a),
in Equation (23) from Equation (3a),
![]() (24)
(24)
By equating the RHS of Equations (2b) and (24)
![]() (25)
(25)
Substituting ![]() for
for ![]() from Equation (7) in Equation (25) we obtain
from Equation (7) in Equation (25) we obtain
![]() (26)
(26)
Substituting Equation (26) for ![]() in Equation (9) yields
in Equation (9) yields
![]() (27)
(27)
Remark
By appropriate change in variables, Equation (1) is transformed into Equation (19) which is a parabolic heat equation to be discretized by the MOL. Equation (27) is the derived approximate theoretical solution to the transformed Black Scholes equation.
3. L-Stable Implicit Trapezoidal-Like Integrator
The trapezoidal-like integrator
![]() (28)
(28)
where
![]() (29a)
(29a)
![]() (29b)
(29b)
![]() are the first and second eigenvalues of the discretization matrix respectively;
are the first and second eigenvalues of the discretization matrix respectively;
![]() is the time step; and
is the time step; and ![]() denotes differentiation with respect to time.
denotes differentiation with respect to time.
The derivation of the method (28) and the analysis of the order of accuracy are as discussed in [29] , while the stability properties of the method are discussed in [30] .
4. Numerical Experimentation
For numerical experimentation the following values were used: k = 0.001, r = 0.1, σ = 0.2, K = 100, T = 1, Δx = 0.01 and Δτ = 0.001.
5. Computation of Absolute and Relative Errors
In this section we explain how the absolute errors and relative errors of the methods shown in Table 1 and Table 2 were obtained.
![]()
Table 1. Solution approximations and errors of the new scheme.
![]()
Figure 1. The graphs of the numerical solution of the new scheme and the theoretical solution.
![]()
Table 2. Solution approximations, errors and relative errors of the new scheme.
5.1. Absolute Errors
The absolute errors of the scheme were computed by the use of the formula:
![]()
where the numerical solution at the grid point ![]() is
is ![]() and the analytical solution at the same grid point is
and the analytical solution at the same grid point is![]() .
.
5.2. Relative Errors
Relative errors of the method were computed by use of the formula:
![]()
where the numerical solution at the grid point ![]() is
is ![]() and the analytical solution at the same grid point is
and the analytical solution at the same grid point is![]() .
.
6. Results and Discussion
On the implementation of the L-stable trapezoidal-like integrator for the solution of transformed Black Scholes equation after discretizing with MOL, the errors and relative errors of the scheme were computed as shown in Table 1 and Table 2 respectively. The trapezoidal-like integrator is an accurate time predictor of the solution of the Black Scholes equation. All computations in this paper were carried out in Maple 15 while the plotting of Figure 1 was carried out in Matlab.
NOTES
*Corresponding author.