Use of an Energy-Like Integral to Study the Motion of an Axi-Symmetric Satellite under Drag and Radiation Pressure ()
1. Introduction
The classical two body problem is one of the most important topics in the field of celestial mechanics, specially the applications of the theory of artificial satellites. Since Brouwer and Hori [1] , so many works have been made to study the problem with different factors considered e.g. Mittleman and Jezewski [2] and Jezewski and Mittleman [3] , Danby [4] , Leach [5] , Gorringe and Leach [6] , McMahon and Scheeres [7] etc.
Marvaganis [8] studied the motion of an almost constant-speed two body problem under the effect of air resistance. The drag force was taken in the form of Danby’s drag, while Marvaganis and Michalakis [9] studied the two body problem in the existence of Danby’s drag and where the bigger body was radiating. They used a Laplace-like integral to derive the orbit equation. El-Shaboury and Mostafa [10] studied the problem of an axi-symmetric satellite under drag and radiation pressure by first neglecting the effect of axi-symmetry of the satellite, and then adding it as a perturbation to the problem.
In this work, an attempt is made to get a solution for the problem of an axi-symmetric satellite under drag and radiation pressures, which all the effects are included in the equation of motion from the beginning by using energy like integral. A relation for the orbit equation is derived first for a general air drag function and then for the case of Danby’s drag. Finally, the solution of an almost constant speed satellite has been given.
2. The Equation of Motion and the Integral of Angular Momentum
The equation of motion of an axi-symmetric satellite under the gravitational force of a spherical body with an additional force due to the resistance force and radiation pressure can be modeled such as Mavraganis and Michalakis (1994), and El-Shaboury and Mostafa (2014).
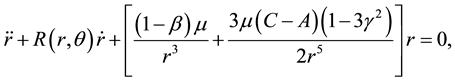 (1)
(1)
The air resistance is taken as a general function R of the polar coordinates , and the definitions of the involved parameters are as following:
, and the definitions of the involved parameters are as following:
 is the gravitational constant.
is the gravitational constant.
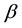 is the radiation constant, where
is the radiation constant, where 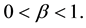
 are the principal moments of inertia of the satellite (
are the principal moments of inertia of the satellite (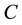 about the symmetric axis), and
about the symmetric axis), and  is the direction cosine of the radius vector with respect to the axis of the satellite. For simplification, we will rename
is the direction cosine of the radius vector with respect to the axis of the satellite. For simplification, we will rename
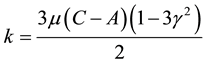
Now, vector product Equation (1) with r, and remembering that 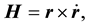 we get,
we get,
 (2)
(2)
which gives immediately,
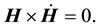
This expression admits a first vector which is the constant direction  of the angular momentum
of the angular momentum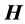 . Therefore the motion is planar. This enables us to simplify Equation (2) by writing
. Therefore the motion is planar. This enables us to simplify Equation (2) by writing
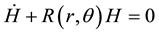 . (3a)
. (3a)
Let the resistance be a general function of the polar angel  divided by the square of the radial distance r, i.e.
divided by the square of the radial distance r, i.e.
![]() (3b)
(3b)
We get,
![]() (4)
(4)
where, h is the constant angular momentum in the absence of the drag force, and![]() .
.
3. The Energy-Like Invariant of Motion
Now, let ![]() be the angle between the radial distance
be the angle between the radial distance ![]() and the distance p of the origin O from the tangent (Figure 1).
and the distance p of the origin O from the tangent (Figure 1).
The vector equation of motion is thus resolved to
![]() (5)
(5)
![]()
Figure 1. Geometrical meaning of the angle φ.
![]() (6)
(6)
where ![]() is the radius of curvature. From the definition of the angle
is the radius of curvature. From the definition of the angle![]() , we have
, we have
![]() (7)
(7)
and using the substitution
![]() (8)
(8)
Equation (5) becomes,
![]() (9)
(9)
This gives,
![]() (10)
(10)
where![]() . It is clear that the above equation gives the energy integral in the absence of resistance, radiation pressure and oblateness. However in the absence of resistance only, we will still have the invariant of motion
. It is clear that the above equation gives the energy integral in the absence of resistance, radiation pressure and oblateness. However in the absence of resistance only, we will still have the invariant of motion
![]() (10a)
(10a)
4. A Relation for the Orbit Equation
Taking R in the form![]() , where
, where ![]() is an arbitrary function of the angle
is an arbitrary function of the angle![]() . Equation (10) gives,
. Equation (10) gives,
![]() , (11)
, (11)
which implies by using Equation (4)
![]() (12)
(12)
In order to integrate the required integration, we expand V in Taylor series of the polar angle![]() ,
,
![]() (13a)
(13a)
![]() (13b)
(13b)
where ![]() is the initial value of
is the initial value of ![]() and
and ![]() Then we have
Then we have
![]()
We write,
![]()
where,
![]()
Thus,
![]() , (14a)
, (14a)
where,
![]() (14b)
(14b)
Therefore, we have the integration,
![]() (15)
(15)
Thus, using Equations (12), (14a), and (15) we get a relation for the orbit equation in the form,
![]() (16)
(16)
where ![]() is given by Equation (14b),
is given by Equation (14b), ![]() is given by Equation (13b) and
is given by Equation (13b) and ![]()
Equation (16) describes a relation for the orbit equation of an axi-symmetric satellite with oblateness coeffi-
cient k under radiation pressure of coefficient ![]() and air drag whose function is given by
and air drag whose function is given by![]() , where
, where
![]() can be chosen arbitrary.
can be chosen arbitrary.
The convergence of the involved series is guaranteed for initial velocity satisfying the vanishing of ![]()
for all n > N, where N can be chosen arbitrary.
4.1. The Case of Danby Drag
In the special case of Danby’s drag (Dabny, 1962), ![]() , and
, and ![]() where
where ![]() is a constant, the required integrations reduce to:
is a constant, the required integrations reduce to:
![]() (17)
(17)
![]() (18)
(18)
Substituting,
![]() (19)
(19)
we get the integration (18) in the form![]() . To evaluate this integral, we distinguish between two cases
. To evaluate this integral, we distinguish between two cases
for n when it is even or odd,
When n is even, we write
![]()
and then we use the expansion
![]()
thus we get
![]()
And when n is odd, we write
![]()
then we use the expansion
![]()
thus we get
![]()
We can collect the two cases together in one case to get,
![]() (20)
(20)
Substituting from Equations (17 - 20) into Equation (16), we get after simplification
![]() (21)
(21)
Equation (21) gives a relation for the orbit equation of an axi-symmetric satellite under the gravitational effect of a radiating body and air resistance described by Danby’s drag.
4.2. The Case of an Almost Constant Speed Satellite
If the satellite is of almost constant speed, then we assume that the first derivative is of small value, and all the higher derivatives to be zero (e.g. Mavraganis, 1991), we get the solution
![]() (22)
(22)
Equation (22) is a special case of Equation (21) when the satellite is of almost constant speed.
5. Conclusions
In this paper, the motion of an axi-symmetric satellite under the effect of a radiating body in the presence of air drag is studied. An energy-like integral for the problem has been evaluated using a Taylor expansion for the velocity around the initial value of the polar angel. The convergence of the integral is guaranteed by the assump-
tion that the derivative ![]() for all n > N, for an arbitrary N.
for all n > N, for an arbitrary N.
The energy-like integral has been used to get a relation for the orbit equation of the satellite. The relation is derived first for a general air drag function and then for the case of Danby’s drag. Finally, the solution of an almost constant speed satellite has been given.