A New Symbolic Algorithm for Solving General Opposite-Bordered Tridiagonal Linear Systems ()
1. Introduction
The 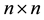 general tridiagonal matrix
general tridiagonal matrix  takes the form:
takes the form:
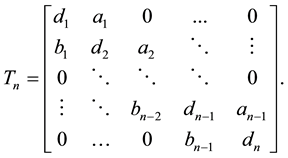 (1)
(1)
The matrix in (1) frequently appears in many applications, for example, in parallel computing, telecommu- nication system analysis, solving differential equations using finite differences, heat conduction and fluid flow problems. The interested reader may refer to [1] - [12] and the references therein.
Inverting tridiagonal matrices in (1) have been considered by many authors. See for instance, [13] - [22] . To study matrices of the form (1) it is advantageous to introduce an n-dimensional vector 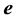 in the following way [23] :
in the following way [23] :
 (2)
(2)
whose components 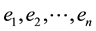 are given by:
are given by:
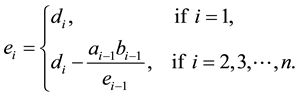 (3)
(3)
The symbolic algorithm DETGTRI [23] is based on (2) and (3). By using the LU factorization of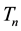 , it is known that [23]
, it is known that [23]
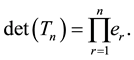 (4)
(4)
There are great interests in solving general opposite-bordered tridiagonal linear system, and hereafter it will be referred to as OBTLS, of the form:
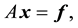 (5)
(5)
in which the coefficient matrix A is given by:
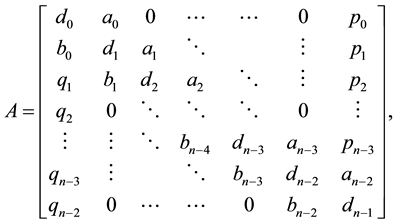 (6)
(6)
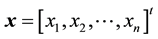 and
and
This system frequently occurs in engineering computation and science, e.g. in the numerical solution of an ablation and heat transfer problem as referred in [24] - [28] . The matrix A in (6) can be stored in  memory locations only.
memory locations only.
In [28] , the author presented a numeric algorithm for solving the linear system (5) with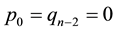 . The algorithm is based on the elementary column operations (ECO’s). It is noted that the numerical algorithm in [28] fails to solve some OBTLS of the form (5). Therefore, the main objective of the present paper is to construct a new symbolic and breakdown-free algorithm for solving the OBTLS in (5).
. The algorithm is based on the elementary column operations (ECO’s). It is noted that the numerical algorithm in [28] fails to solve some OBTLS of the form (5). Therefore, the main objective of the present paper is to construct a new symbolic and breakdown-free algorithm for solving the OBTLS in (5).
Throughout this paper, the word “simplify” means simplifying the algebraic expression under consideration to its simplest rational form. Also,  is a formal parameter which can be treated as a symbolic name whose actual value is 0 as we will see later.
is a formal parameter which can be treated as a symbolic name whose actual value is 0 as we will see later.
The organization of the paper is as follows. The main results are given in the next section. Some illustrative examples are given in Section 3. In Section 4, we present some concluding remarks.
2. Main Results
In this section, we are going to formulate a new algorithm for solving OBTLS of the form (5). We begin by considering the singly bordered tridiagonal linear systems of the form (7)-(8) below.
2.1. A Symbolic Algorithm for Solving Singly Bordered Tridiagonal Linear Systems
The 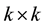 singly bordered tridiagonal linear system takes the form:
singly bordered tridiagonal linear system takes the form:
![]() (7)
(7)
where
![]() (8)
(8)
![]() and
and
The Doolittle LU factorization of ![]() is given by [1] :
is given by [1] :
![]() (9)
(9)
where
![]() (10)
(10)
and
![]() (11)
(11)
where the quantities ![]()
![]() and
and ![]() are given, respectively, by:
are given, respectively, by:
![]() (12)
(12)
![]() (13)
(13)
and
![]() (14)
(14)
It follows from (9)-(11) that
![]() (15)
(15)
At this point, it should be mentioned that the above ![]() factorization is always possible even if the matrix
factorization is always possible even if the matrix ![]() is singular.
is singular.
The solution of the system in (7) reduces to solving the two standard linear systems:
![]() (16)
(16)
and
![]() (17)
(17)
We are now ready to formulate the following algorithm for solving the linear system (7).
![]()
2.2. A Symbolic Algorithm for Solving General OBTLS
In order to solve the general OBTLS (5) it is convenient to introduce the following notations:
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
![]()
and
![]()
Based on the above notations, the linear system in (5) can be written in the partitioned form:
![]() (21)
(21)
The solution of the linear system (21), may be obtained by solving the two linear systems:
![]() (22)
(22)
![]() (23)
(23)
It is not difficult to prove that:
![]() (24)
(24)
As can be seen from (24), we need to compute ![]() and
and ![]() By solving the following singly bordered systems with two right-hand sides we obtain the solution vectors
By solving the following singly bordered systems with two right-hand sides we obtain the solution vectors ![]() and
and![]() :
:
![]() (25)
(25)
Consequently, we have from (24)
![]() (26)
(26)
and
![]() (27)
(27)
By substituting (26) and (27) into (22), it follows that
![]() (28)
(28)
Therefore, we get
![]() (29)
(29)
Hence, the solution vector of the OBTLS (5) is ![]()
The proofs of the following result may be found in [29] .
Theorem 1. (Schur determinant identity) Let ![]() and
and ![]() are
are ![]()
![]()
![]() and
and ![]() matrices, respectively. Let
matrices, respectively. Let ![]() be a
be a ![]() block matrix given by
block matrix given by
![]() (30)
(30)
Then
![]()
By noticing (21), we see that the matrix ![]() in (6) can be written in the partitioned form:
in (6) can be written in the partitioned form:
![]() (31)
(31)
Hence, by applying Theorem 1 on this matrix, we get the following result:
Corollary 1. Let ![]() be the
be the ![]() matrix given in (31), then the determinant of
matrix given in (31), then the determinant of ![]() is given by:
is given by:
![]() (32)
(32)
provided ![]() is a nonsingular matrix.
is a nonsingular matrix.
The main result of the present paper may now be formulated as follows:
![]()
This algorithm will be referred to as the OBS algorithm. The computational cost for OBS is ![]() in terms of total number of flops, where each flop represents one of the four basic arithmetic floating point operations.
in terms of total number of flops, where each flop represents one of the four basic arithmetic floating point operations.
A MATLAB code based on the OBS algorithm is available upon request from the authors.
3. Illustrative Examples
In this section we are going to consider some illustrative examples. The, symbolic computations are performed in Example 1 by using MATLAB with Symbolic Math Toolbox. Also, we compare the proposed algorithm with MATLAB back-slash and the algorithm in [28] by means of execution times and accuracy of the solutions in Example 2. Finally, we give Example 3 in order to demonstrate the validity of the OBS algorithm. All experiments were carried out using MATLAB 7.10.0.499 (R2010a) on a PC with Intel(R) Core(TM) i7-3770 CPU processor.
Example 1. Solve the opposite-bordered tridiagonal linear system:
![]() (33)
(33)
Solution.
Here, ![]()
![]()
![]()
![]()
![]()
![]() and
and
![]()
The numeric algorithm in [28] fails to solve the linear system (33) although ![]() Applying the OBS algorithm, we obtain:
Applying the OBS algorithm, we obtain:
![]()
![]() (Step 1).
(Step 1).
![]() (Step 2) and
(Step 2) and
![]() (Step 3).
(Step 3).
The solution vector ![]() (Step 4).
(Step 4).
Example 2. Consider the opposite-bordered tridiagonal linear system:
![]() (34)
(34)
The exact solution of this system is ![]() Table 1 shows the CPU times (after 100 tests) ob-
Table 1 shows the CPU times (after 100 tests) ob-
tained from the OBS algorithm, the algorithm in [28] and MATLAB back-slash operator for n = 1000, 2000, ![]() , 10,000. The absolute errors
, 10,000. The absolute errors ![]() are shown in Figure 1. Here,
are shown in Figure 1. Here, ![]() is the Euclidean vector norm.
is the Euclidean vector norm.
Example 3. Consider the opposite-bordered tridiagonal linear system:
![]() (35)
(35)
Table 2 gives the absolute errors and CPU times (after 100 tests) obtained from the OBS algorithm for n = 1000, 5000, 10,000, 20,000, 30,000, 40,000, 50,000.
![]()
Table 1. Mean value of the CPU times after 100 tests.
![]()
Figure 1. Absolute errors for Example 2.
![]()
Table 2. Absolute errors and CPU times of Example 3 for the OBS algorithm.
4. Conclusion
In this paper, we proposed a new efficient and reliable algorithm for solving general opposite-bordered tridia- gonal linear systems in linear time. An explicit formula for computing the determinant of an opposite-bordered tridiagonal matrix is obtained. Some illustrative examples are given.
Acknowledgements
The authors wish to thank anonymous referees and the editorial board of the AJCM for careful reading of the manuscript and their useful comments.
NOTES
*Corresponding author.