Application of Null Space Based Behavior Control to the Swarm Robot’s Control ()
1. Introduction
The swarm robots, a new research trend with many promising technologies in the field of robotics, particularly have high intellect, but do not require the complex manufacturing technology. The swarms are increasingly interested in the study, although each study has given specific research goals. The research of the converging process plays an important role in swarm robots. V. Gazi, Kevin M. Passino [1] considered the number of individuals-M in n-dimensional Euclidean space, the assumption of uniformity and visibility between individuals is not limited. The move of the individuals depends on the attraction/repulsion forces which are explicit mathematical functions. The authors have demonstrated the stability of the swarm: all the individuals will be located in a certain area after the period of time of moving. [2] and [3] also provided attraction/repulsion functions which are explicit functions similar to [1] , but [2] developed the model based on the interaction from the individual to another, or between the individual and the environment. The model designed [2] stands for seeking food, and the results are simulated in 3D space. [3] analyzed the stability of the swarm, attraction/repulsion forces between individuals will be 0 if they do not see each other (apart from the impact of the sensor) and the forces are only equal to g (.) when the individuals are neighboring. Second difference [3] is the limit move of each individual and the move and has an effect on the convergence of swarm. Therefore, the model [3] stands for a model of actual biological swarm. When the swarm robots move in an environment with obstacles, they have to avoid ecollising obstacles. Avoid y obstacles has been studying extensively and many control algorithms solving this problem have been proposed. However, most of these algorithms are constituted on the basis of a single robot, the size and mass areas large as [4] [5] .
In content of this paper, firstly we proposed a solution to control swarm robots to avoid obstacles and moving to the goal, then analyzed the stability of the swarm and finally, we conducted the algorithm on Matlab software.
2. Model Swarm Robot by the Method of Null Space Based Behavior Control
2.1. The Swarm Robots Perform a Task
Consider the swarm robots of N individuals move in two dimensions, given : is the position and
: is the position and : is velocity vector of movement of the i―individual (i = 1 ÷ N), then the mathematical model of the i-individual is described as follows:
: is velocity vector of movement of the i―individual (i = 1 ÷ N), then the mathematical model of the i-individual is described as follows:
 (1)
(1)
Given s is the variables are controlled to complete objectives
 (2)
(2)
The derivative (2) in time:
 (3)
(3)
To combine (1) và (3): 
where: J(p) is Jacobian matrix, 
Inferring:
 (4)
(4)
where: J+ known as pseudo inverse matrix, 
Call the disachieveable desired distance, then (4) is rewritten as follows:
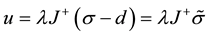 (5)
(5)
where: l factor is positive, .
.
The null projector matrix Nn is a projector onto the null space of J: 
2.2. The Swarm Robots Perform Multiple Tasks
Consider the case swarm robots perform tasks move to the goal, on moving them to avoid obstacles lie in the way to avoid being damaged. Now each individual robot must perform three tasks:
-The first task: to avoid obstacles.
-The second task: to move to the goal.
-The third task: to maintain swarm.
To control the robot performs the above tasks, the supervisor can choose the priority level of the task. In this article, we chose the priority level order: avoid obstacles, moving to goal and maintain swarm. NSB control [6] , which the is technique control was designed to be based on hierarchical priority of the task: by projecting the lower priority task on the null space of higher priority tasks, a diagram of velocity synthetic of the robot is shown in Figure 1.
Determine the speed to avoid obstacles:
![]()
Figure 1. Diagram of velocity synthetic of the i-robot.
Given : the position of static obstacles,
: the position of static obstacles, : the distance between the i-robot and obstacle is determined by the formula:
: the distance between the i-robot and obstacle is determined by the formula: .
.
The desire of the robot control is to avoid obstacles: if obstacles are on the robot moves to the goal, the robot must will be far from obstacles a safe distance![]() ; if an obstacle is out of robot’s movement then the obstacle does not affect the speed of movement of the robot. It means that the moving speed of the robot individual depends on the distance between the robot and obstacle.
; if an obstacle is out of robot’s movement then the obstacle does not affect the speed of movement of the robot. It means that the moving speed of the robot individual depends on the distance between the robot and obstacle.
Jacobian matrix![]() : performance the moves of robot’s velocity vector avoides obstacles
: performance the moves of robot’s velocity vector avoides obstacles
![]() (6)
(6)
Pseudo inverse of matrix Jo:![]() ,
,![]() .
.
The null projector matrix of Jo:
![]() , (7)
, (7)
From (5) inferred the velocity vector of the robot to avoid obstacles are identified as follows:
![]() (8)
(8)
where: ![]() the error between the actual distance and the desired distance.
the error between the actual distance and the desired distance.
Determine the velocity of moves to the goal:
Similar to calculate velocity avoid moving to the goal: ![]() is the position of the goal to be reached, sg Î R the distance between the ith robot and the goal is determined by the formula:
is the position of the goal to be reached, sg Î R the distance between the ith robot and the goal is determined by the formula:
![]()
The desire control the robot’s move toward the goal is the distance from the robot to the goal![]() .
.
Matrix Jacobian![]() :
:
![]() (9)
(9)
Pseudo inverse of matrix Jg: ![]()
The null projector matrix of Jg:
![]() , (10)
, (10)
From (5) inferred the velocity vector of the robot movement to the goal are defined as follows
![]() (11)
(11)
where: ![]() the error between the actual distance and the desired distance.
the error between the actual distance and the desired distance.
Determine the velocity of move maintain swarm:
In swarm robots, maintain the swarm is a very important task, many of the scientific research on this problem, but in the [7] , we have analyzed the convergence behavior of the swarm based on laws attraction/repulsion fuzzy. The physical significance of our model is clear. If an individual is close to the others in the swarm, the repulsion dominates, which ensures the individual far away from them enough to be “safe”. The repulsion increases as any two individuals get closer because in the real nature the individuals are inclined to be more apart away from others if they are nearer. If an individual is far away from others in the swarm, the attraction dominates, which makes the individual get closer to the other members of the swarm. However, as the distance between the individual and the others gets bigger, this individual will loss more connection to other members of the swarm, and thus, the attraction decreases to zero as the distance increases to infinity. The attraction/repulsion function is built based on fuzzy logic. The distance between the i-robot and the j-robot (j = 1 ÷ N, j ≠ i) is:
![]()
The purpose of the control is maintains distance between individuals in the swarm always equal a constant:
![]() ,
,
In [7] , the kinetic model of the i?individual is built as follows:
![]() (12)
(12)
where: ![]() the interaction forces between the robot pair (i, j), this function is built on the basis of fuzzy logic:
the interaction forces between the robot pair (i, j), this function is built on the basis of fuzzy logic:
![]() (13)
(13)
Matrix Jacobian:
![]() (14)
(14)
Pseudo inverse of matrix Js:
![]() (15)
(15)
The null projector matrix of Js:
![]() , (16)
, (16)
From (5) inferred to maintain the velocity vector of the robot swarm is defined as follows:
![]() (17)
(17)
Integrated velocity when the robot perform all three tasks:
The desired control (velocities) are:
![]() (18)
(18)
where:![]() ;
;![]() .
.
3. Analyzing the Stability of Robot Swarm by the Method of Null Space Based Behavior Control Lemma
Let ![]() be a symmetric matrix and x, y are vectors with appropriate dimension. Denote
be a symmetric matrix and x, y are vectors with appropriate dimension. Denote ![]() the smallest and largest eigenvalue of matrix A. Then:
the smallest and largest eigenvalue of matrix A. Then: ![]() and
and![]() .
.
Proof.
Let denote ![]() are the eigenvalues of matrix A. There is a set of orthonormal base
are the eigenvalues of matrix A. There is a set of orthonormal base ![]() such
such![]() . The vector
. The vector ![]() can be described as:
can be described as:![]() .
.
Then: ![]()
So we have:
![]()
Therefore: ![]() or:
or:![]() .
.
On the other side, we have:
![]() or:
or:
Then:
![]()
Theorem:
The necessary and sufficient condition of asymptotically stable task error vector ![]() is the Jacobians associated with obstacle avoidance o and reach goal g tasks and the Jacobians associated with separation task and the augmented task og satisfy the independence condition:
is the Jacobians associated with obstacle avoidance o and reach goal g tasks and the Jacobians associated with separation task and the augmented task og satisfy the independence condition:
![]() (19)
(19)
where ![]() denotes the rank of the matrix.
denotes the rank of the matrix.
Proof.
A possible Lyapunov function candidate ![]() continuously differentiable is given by
continuously differentiable is given by![]() , whose time derivative is:
, whose time derivative is:
![]()
![]()
![]() (20)
(20)
due to the fact that:![]() .
.
We have to prove that the function: ![]() is positive definite.
is positive definite.
Firstly, it is not difficult to claim that a necessary condition of the positive definiteness of V1 is that two first elements on the main diagonal ![]() and the function
and the function ![]() is positive definite. The element
is positive definite. The element ![]() is obviously positive as along as the gain
is obviously positive as along as the gain![]() . The element
. The element ![]() is positive if the obstacle avoidance and reach goal tasks are independent, i.e., if condition (19) hold and the gain
is positive if the obstacle avoidance and reach goal tasks are independent, i.e., if condition (19) hold and the gain![]() . The function
. The function ![]() is positive definite if the matrix
is positive definite if the matrix ![]() is positive definite. To prove it let define the eigenvalues of the symmetric positive definite matrix
is positive definite. To prove it let define the eigenvalues of the symmetric positive definite matrix ![]() as
as![]() . Then we can rewrite:
. Then we can rewrite:
![]()
Note that due to the fact that:
![]()
so we have: ![]()
Therefore ![]() is positive definite.
is positive definite.
The ![]() submatrix M33 is positive definite if the separation task is independent to the augmented Jacobian obtained by stacking obstacle avoidance and reach goal tasks.
submatrix M33 is positive definite if the separation task is independent to the augmented Jacobian obtained by stacking obstacle avoidance and reach goal tasks.
The sufficient conditions of the theorem follow from the following fact.
In the formula:
![]() (21)
(21)
directly we have:![]() ;
;
![]()
![]()
and (see Lemma): ![]()
![]()
![]()
where: ![]() -the largest singular value of the matrix
-the largest singular value of the matrix![]() ,
, ![]() -the largest singular value of the matrix
-the largest singular value of the matrix![]() .
.
So V1 can be underestimated as:
![]()
It is convenient to rewrite the relation above to the matrix formalism:
![]()
where the matrix ![]() is defined as:
is defined as:
![]() (22)
(22)
Order to ![]() is positive definite then
is positive definite then ![]() is positive definite, which means that that, having the scalar diagonal elements positive, is always positive definite according to Sylvester theorem:
is positive definite, which means that that, having the scalar diagonal elements positive, is always positive definite according to Sylvester theorem:
![]() (23)
(23)
![]() (24)
(24)
![]() (25)
(25)
From (7): ![]() according to Cauchy- Schwarz theorem:
according to Cauchy- Schwarz theorem:![]() therefore
therefore![]() , equal sign occurs if and only if Jo and Jg are
, equal sign occurs if and only if Jo and Jg are
two vectors to linear dependence, ![]() if and only if Jo and Jg are two linearly independent vectors. In other words, (24) correct then the first equation of (19) is also true. Similarly,
if and only if Jo and Jg are two linearly independent vectors. In other words, (24) correct then the first equation of (19) is also true. Similarly, ![]() if and only if Jog and Js are two linearly independent vectors, it is means (25) correct then the second equation of (19) is also true.
if and only if Jog and Js are two linearly independent vectors, it is means (25) correct then the second equation of (19) is also true.
The theorem has been proved.
4. Simulation
In this section, we will give some simulation results for illustrating the analytical results. For each simulation, the search space is set [500, 500]. The initial positions for the robots, obstacles, goal are randomly generated. For the NSB search in this paper, N robots are used to search a single goal.
Figure 2(a) and Figure 2(b) shows the paths taken by the individual robots to converge at the goal using method of Null Space based Behavior control when the gains lo is always negative definite and lg is always positive definite. It’s sure that the control algorithm following three goal tacks is:
1) Firtly: to avoid obstacles,
2) Secondly: to move to the goal,
3) Thirdly: to maintain swarm.
When lo is positive definite or lg are negative definite, apparently through Figure 2(c)) we can observer that a few robots unavoidable obstacle or swarm not converged at the goal (Figure 2(d)).
![]() (a) (b) (c) (d)
(a) (b) (c) (d)
Figure 2. Simulation results the process of moving of the swarm robots to the goal. (a) N = 21, lo = −1.5, lg = 0.05; (b) N = 41, lo = −0.5, lg = 0.05; (c) N = 21, lo = 0.5, lg = 0.05; (d) N = 13, lo = −1.5, lg = −0.05.
Simulation results have confirmed the correctness of the algorithm and stable conditions of the implementation process of the mission objectives.
5. Conclusion
This paper proposed a control solution to the swarm robot by constituting the method of NSB control and built the control law, simultaneously proved the convergence of algorithm based on Lyapunov theory. Simulation results show that: the swarm robots avoided obstacles and found the goal after moving in a determined time. The results of this paper show that applying of NSB to solve collective search problem in the obstacle environment is very practical and efficient. In the future, we are going to consider the swarm robots operate in an environment with more rugged terrain, can be utilized for hazardous tasks such as landmine detection, fire fighting, military surveillance.