Modified Tunneling Radiation of Fermions from a Spherically Symmetric Spacetime with Dark Matter ()
1. Introduction
Based on the quantum effect, people found that the black holes can radiate particles [1]. The radiation of black hole got researchers attention, many new methods were presented to study it [2]-[4]. Parikh and Wilzcek put forward the quantum tunneling method, which was an effective method to discuss the black hole’s Hawking radiation. With the help of the quantum tunneling method, they have calculated the massless scalar particle’s tunneling rate and Hawking temperature of the spherically symmetrical spacetime [5]. Then, Kerner and Mann developed the quantum tunneling method and studied the fermions tunneling from Schwarzschild (SC) spacetime [6]. Later, the tunneling behavior of particles with 0 spin, 1/2 spin, 1 spin and 3/2 spin from black holes were investigated via Hamilton-Jacobi ansatz, which is another quantum tunneling method. However, the results obtained in previous work showed that the standard Hawking temperature of black holes was inverse to their mass. As Hawking announced, the black hole would emit all their mass as the temperature increase, this process causes the black holes evaporate over. In other words, black holes would loss all their information, which was called as information paradox of black hole [7] [8].
In order to solve the information paradox problem, people proposed many kinds of correction theories. Recently, people studied the physical properties of the black hole via the generalized uncertainty principle (GUP) [9]-[11]. In quantum gravity theory and string theory, people believe the existence of the minimal observable length, which can be described by the GUP [12] [13] . In [ 14 ], based on the associative Heisenberg algebra
 , where
, where  is the momentum operator and
is the momentum operator and  is the position operator. One kind of GUP is expressed as
is the position operator. One kind of GUP is expressed as
 (1)
(1)
with  is a small value, which represents the effects of quantum gravity,
is a small value, which represents the effects of quantum gravity, 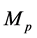 being the Planck
being the Planck
mass [15]. Adopted GUP, Banerjee and Ghosh investigated the thermodynamics of SC spacetime, their results showed that the black hole have remnant mass at the end of evolution [16]. Soon, combining with quantum tunneling method and GPU, the Hawking radiation of Schwarzschild black hole was studied by Nozari and Saghafi [17].
On other hand, astronomers predict 27% of the universe is dark matter. It is natural to think how can the dark matter influence the properties of black hole and whether different corrected methods deduce different results? In this paper, we will apply the GUP to investigate the Hawking temperature and entropy of spherically symmetric black hole with dark matter.
The remainder of the paper goes as follows. In Section 2, we overview of the spherically symmetric black hole with dark matter is provided. In Section 3, we corrected the Hawking temperature and entropy via GUP. The last section is the discussion and concludes.
2. The Spherically Symmetric Spacetime with Dark Matter
In curved space-time, the line element of spherically symmetric black hole with dark matter can be expressed as [18] [19]
 (2)
(2)
where
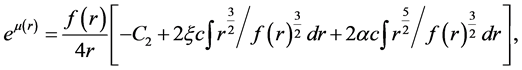 (3)
(3)
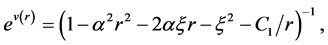 (4)
(4)
 (5)
(5)
In Equation (3)-Equation (5), the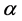 ,
, 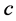 ,
, 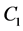 ,
, 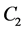 are parameters of the spacetime, note that
are parameters of the spacetime, note that  is a parameter of cold dark matter. In order to discuss the tunneling of the black hole, here we let parameter
is a parameter of cold dark matter. In order to discuss the tunneling of the black hole, here we let parameter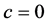 ,
, 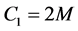 ,
, ![]() , Equation (3) and Equation (4) become to
, Equation (3) and Equation (4) become to
![]() (6)
(6)
Note that Equation (5) and Equation (6) have the same expression. Thus, one can use ![]() to replace
to replace ![]() and
and![]() . Now, the metric of spherically symmetric black hole with dark matter is given by
. Now, the metric of spherically symmetric black hole with dark matter is given by
![]() (7)
(7)
The horizons of this black hole are determined by null super-surface equation. Now, assuming![]() , by a simple calculate, the roots can be expressed as
, by a simple calculate, the roots can be expressed as![]() ,
, ![]() and
and![]() . According to the three roots,
. According to the three roots, ![]() can be written as
can be written as
![]() (8)
(8)
where ![]() is the cosmological horizon,
is the cosmological horizon, ![]() is the outer event horizon and
is the outer event horizon and ![]() is the inner event horizon. The three roots satisfy
is the inner event horizon. The three roots satisfy![]() .
.
3. The GUP Corrected Hawking Temperature and Entropy of Spherically Symmetric Black Hole with Dark Matter
According to the GUP, Chen et al. have rewritten the original Dirac equation into generalized form. The massless generalized Dirac equation in curved spacetime is [20]
![]() (9)
(9)
In order to discussing the fermions tunneling from black hole, people assume fermions with 1/2 spin have two states: spin up state and spin down state. Here we only consider the spin up state. The wave function of the spin up state is
![]() (10)
(10)
where ![]() is the action of up spin state of fermions, which can be expanded in powers of
is the action of up spin state of fermions, which can be expanded in powers of![]() .
.![]() ,
, ![]() are functions of coordinates
are functions of coordinates![]() . In order to solve Equation (9), one needs to find a tetrad, which can construct a gamma matrix. The tetrad is
. In order to solve Equation (9), one needs to find a tetrad, which can construct a gamma matrix. The tetrad is
![]() (11)
(11)
Then, the ![]() matrices are
matrices are
![]() (12)
(12)
In Equation (12), ![]() and
and![]() ,
, ![]() are Pauli matrices. Substituting Equation (10) and Equation (12) into Equation (9), then using WKB approximation and ignoring the higher order of
are Pauli matrices. Substituting Equation (10) and Equation (12) into Equation (9), then using WKB approximation and ignoring the higher order of![]() , one gets four Hamilton-Jacobi equations
, one gets four Hamilton-Jacobi equations
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
where![]() . For solving the four equations above, one needs to carry out separation of variables of
. For solving the four equations above, one needs to carry out separation of variables of![]() . Adopting the following ansatz for the separation of variables
. Adopting the following ansatz for the separation of variables
![]() (17)
(17)
where ![]() being the energy of this tunneling particle. One finds that Equation (15) and Equation (16) can be decoupled into the purely angular equation
being the energy of this tunneling particle. One finds that Equation (15) and Equation (16) can be decoupled into the purely angular equation
![]() (18)
(18)
In Equation (18), the ![]() is a small coefficient associated with quantum gravity effective, it cannot be zero. Thus, we get an important relation
is a small coefficient associated with quantum gravity effective, it cannot be zero. Thus, we get an important relation
![]() (19)
(19)
Now, substituting Equation (17) and Equation (19) into Equation (15) and Equation (16), keep the first order term of![]() , yields
, yields
![]() (20)
(20)
where ![]()
![]()
![]() . Neglecting the higher order term of
. Neglecting the higher order term of ![]() and solving Equation (20) at the outer event horizon. The result of Equation (20) is
and solving Equation (20) at the outer event horizon. The result of Equation (20) is
![]() (21)
(21)
The plus (minus) means the outgoing (ingoing) wave. Here we only keep the imaginary part of Equation (24), because the real part ![]() do not contribution to calculate the tunneling rate. The tunneling rate of fermions is
do not contribution to calculate the tunneling rate. The tunneling rate of fermions is
![]() (22)
(22)
Comparing with the Boltzman factor expression, the GUP corrected Hawking temperature of the black hole with dark matter is
![]() (23)
(23)
![]() (24)
(24)
Then, near the event horizon of the black hole, the position uncertainty of a particle can be expressed [21] [22]
![]() (25)
(25)
where ![]() is a calibration factor and
is a calibration factor and ![]() is the event horizon of the black hole [23]. With the help of Equation (25), The temperature can be written as
is the event horizon of the black hole [23]. With the help of Equation (25), The temperature can be written as
![]() (26)
(26)
In above equation, we set![]() . Obviously, the GUP corrected temperature is lower than the semi-clas- sical case. Besides, it is not only determined by parameters of
. Obviously, the GUP corrected temperature is lower than the semi-clas- sical case. Besides, it is not only determined by parameters of![]() ,
, ![]() and
and ![]() the
the![]() , which belongs to the effects of quantum gravity.
, which belongs to the effects of quantum gravity.
4. Conclusions
In the previous work, people found that the GUP can cause the remnants of black holes. For calculating the remnants, we need neglect the parameters of![]() ,
,![]() . The metric of SC black hole is recovered, Equation (26) becomes to
. The metric of SC black hole is recovered, Equation (26) becomes to![]() . When considering
. When considering ![]() with
with ![]() and
and ![]() , the temperature of black hole will stop increasing. The remnants are
, the temperature of black hole will stop increasing. The remnants are
![]() (27)
(27)
where![]() . Equation (27) implies that the remnant mass and temperature are relate to the Planck mass
. Equation (27) implies that the remnant mass and temperature are relate to the Planck mass ![]() and the dimensionless parameter
and the dimensionless parameter![]() .
.
In this work, with the help of GUP, we corrected the thermodynamic properties of spherically symmetric black hole with dark matter. We find that the GUP corrected temperatures is related to the properties of black hole (mass of black hole, ![]() and dark matter
and dark matter![]() ), and
), and![]() , which represents the effects of quantum gravity. In addition, we can obtain the same result when consider the down spin state of fermions. It implies that the GUP may solve the information paradox of the black hole.
, which represents the effects of quantum gravity. In addition, we can obtain the same result when consider the down spin state of fermions. It implies that the GUP may solve the information paradox of the black hole.
Acknowledgements
This work is supported in part by the Natural Science Foundation of China (Grant No. 11178018).