From Nonparametric Density Estimation to Parametric Estimation of Multidimensional Diffusion Processes ()
1. Introduction
Diffusion processes are widely used for modeling purposes in various fields, especially in finance. Many papers are devoted to the parameter estimation of the drift and diffusion coefficients of diffusion processes by discrete observation. As a diffusion process is Markovian, the maximum likelihood estimation is the natural choice for parameter estimation to get consistent and asymptotical normally estimator when the transition probability density is known [1] . However, in the discrete case, for most diffusion processes, the transition probability density is difficult to calculate explicitly which prevents the use of this method. To solve this problem, several methods have been developed such as the approximation of the likelihood function [2] [3] , the approximation of the transition density [4] , schemes of approximation of the diffusion [5] or methods based on martingale estimating functions [6] .
In this paper, we study the multidimensional diffusion model
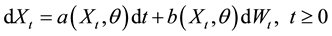
under the condition that  is positive recurrent and exponentially strong mixing. We assume that the diffusion process is observed at regular spaced times
is positive recurrent and exponentially strong mixing. We assume that the diffusion process is observed at regular spaced times  where
where  is a positive constant. Using the density of the invariant distribution of the diffusion, we construct an estimator of θ based on minimum Hellinger distance method.
is a positive constant. Using the density of the invariant distribution of the diffusion, we construct an estimator of θ based on minimum Hellinger distance method.
Let  denote the density of the invariant distribution of the diffusion. The estimator of
denote the density of the invariant distribution of the diffusion. The estimator of 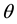 is that value (or values)
is that value (or values) 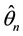 in the parameter space
in the parameter space  which minimizes the Hellinger distance between
which minimizes the Hellinger distance between 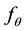 and
and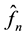 , where
, where 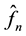 is a nonparametric density estimator of
is a nonparametric density estimator of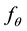 .
.
The interest for this method of parametric estimation is that the minimum Hellinger distance estimation method gives efficient and robust estimators [7] . The minimum Hellinger distance estimators have been used in parameter estimation for independent observations [7] , for nonlinear time series models [8] and recently for univariate diffusion processes [9] .
The paper is organized as follows. In Section 2, we present the statistical model and some conditions which imply that 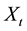 is positive recurrent and exponentially strong mixing. Consistence and asymptotic normality of the kernel estimator of the density of the invariant distribution are studied in the same section. Section 3 defines the minimum Hellinger distance estimator of
is positive recurrent and exponentially strong mixing. Consistence and asymptotic normality of the kernel estimator of the density of the invariant distribution are studied in the same section. Section 3 defines the minimum Hellinger distance estimator of 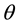 and studies its properties (consistence and asymptotic normality). Section 4 is devoted to some examples and simulations. Proofs of some results are presented in Appendix.
and studies its properties (consistence and asymptotic normality). Section 4 is devoted to some examples and simulations. Proofs of some results are presented in Appendix.
2. Nonparametric Density Estimation
We consider the d-dimensional diffusion process solution of the multivariate stochastic differential equation:
 (1)
(1)
where 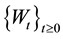 is a standard l-dimensional Wiener process,
is a standard l-dimensional Wiener process, ![]() is an unknown parameter which varies in a compact subset
is an unknown parameter which varies in a compact subset ![]() of
of![]() ,
, ![]() is the drift coefficient and
is the drift coefficient and ![]() is the diffusion coefficient.
is the diffusion coefficient.
We assume that the functions a and b are known up to the parameter ![]() and b is bounded.
and b is bounded.
We denote by ![]() the unknown true value of the parameter.
the unknown true value of the parameter.
For a matrix![]() , the notation
, the notation ![]() denote the transpose of the matrix A. We will use the notation
denote the transpose of the matrix A. We will use the notation ![]() to denote a vectorial norm or a matricial norm.
to denote a vectorial norm or a matricial norm.
The process ![]() is observed at discrete time
is observed at discrete time ![]() where
where ![]() is a positive constant.
is a positive constant.
We make the following assumptions on the model:
(A1): there exists a constant C such that
![]()
(A2): there exist constants ![]() and
and ![]() such that
such that
![]()
(A3): the matrix function ![]() is non degenerate, that is
is non degenerate, that is
![]()
Assumptions (A1)-(A3) ensure the existence of a unique strong solution for the Equation (1) and an invariant measure for the process ![]() that admits a density with respect to the Lebesgue measure and the strong mixing property for
that admits a density with respect to the Lebesgue measure and the strong mixing property for ![]() with exponential rate [10] -[12] . We denote by
with exponential rate [10] -[12] . We denote by ![]() the strong mixing coefficient.
the strong mixing coefficient.
In the sequel, we assume that the initial value ![]() follows the invariant law; which implies that the process
follows the invariant law; which implies that the process ![]() is strictly stationary.
is strictly stationary.
We consider the kernel estimator ![]() of
of ![]() that is,
that is,
![]()
where ![]() is a sequence of bandwidths such that
is a sequence of bandwidths such that ![]() and
and ![]() as
as ![]() and
and ![]() is a non negative kernel function which satisfies the following assumptions:
is a non negative kernel function which satisfies the following assumptions:
(A4)
(1) There exists ![]() such that
such that![]() ,
,
(2) ![]() and
and ![]() as
as![]() ,
,
(A5) ![]() and
and ![]() for
for![]() .
.
We finish with assumptions concerning the density of the invariant distribution:
(A6) ![]() is twice continuously differentiable with respect to
is twice continuously differentiable with respect to![]() .
.
(A7) ![]() implies that
implies that ![]() for all
for all![]() .
.
Properties (consistence and asymptotic normality) of the kernel density estimator are examined in the following theorems. The proof of the two theorems can be found in the Appendix.
Theorem 1. Under assumptions (A1)-(A4), if the function ![]() is continuous with respect to x for all
is continuous with respect to x for all![]() , then for any positive sequence
, then for any positive sequence ![]() such that
such that ![]() and
and ![]() as
as![]() ,
, ![]() almost surely.
almost surely.
Theorem 2. Under assumptions (A1)-(A6), if ![]() is such that
is such that ![]() as
as ![]() then the limiting
then the limiting
distribution of ![]() is
is ![]() where
where
![]()
3. Estimation of the Parameter
The minimum Hellinger distance estimator of ![]() is defined by:
is defined by:
![]()
where
![]()
Let ![]() denote the set of squared integrable functions with respect to the Lebesgue measure on
denote the set of squared integrable functions with respect to the Lebesgue measure on![]() .
.
Define the functional ![]() as follows: let
as follows: let ![]() and denote:
and denote:
![]()
where ![]() is the Hellinger distance.
is the Hellinger distance.
If ![]() is reduced to an unique element, then
is reduced to an unique element, then ![]() is defined as the value of this element. Elsewhere, we choose an arbitrary but unique element of
is defined as the value of this element. Elsewhere, we choose an arbitrary but unique element of ![]() and call it
and call it![]() .
.
Theorem 3. (almost sure consistency)
Assume that assumptions (A1)-(A4) and (A7) hold. If for all![]() ,
, ![]() is continuous at
is continuous at![]() , then for any positive sequence
, then for any positive sequence ![]() such that
such that ![]() and
and![]() ,
, ![]() converges almost surely to
converges almost surely to ![]() as
as![]() .
.
Proof. By Theorem 1, ![]() almost surely.
almost surely.
Using the inequality ![]() for
for![]() , we get
, we get
![]()
Since
![]()
![]() almost surely [13] [14] .
almost surely [13] [14] .
By theorem 1 [7] , ![]() uniquely on
uniquely on![]() ; then the functional T is continuous at
; then the functional T is continuous at ![]() in the Hellin-
in the Hellin-
ger topology. Therefore ![]() almost surely.
almost surely.
This achieves the proof of the theorem.
Denote
![]()
when these quantities exist. Furthermore, let
![]()
To prove asymptotic normality of the estimator of the parameter, we begin with two lemmas.
Lemma 1. Let ![]() be a subset of
be a subset of ![]() and denote
and denote ![]() the complementary set of
the complementary set of![]() . Assume that
. Assume that
(1) assumptions (A1)-(A5) are satisfied,
(2) ![]() is twice continuously differentiable with respect to
is twice continuously differentiable with respect to ![]() and
and
![]()
(3) ![]()
(4) ![]()
then for any positive sequence ![]() such that
such that![]() , the limiting distribution of
, the limiting distribution of
![]()
The proof can be found in the Appendix.
Remark 1. The two dimensional stochastic process (see Section 4) with invariant density
![]() , ,
, ,
where![]() , satisfies the conditions of Lemma 1 with for example
, satisfies the conditions of Lemma 1 with for example ![]() a subset of
a subset of ![]() where
where![]() .
.
Lemma 2. Let ![]() be a compact set of
be a compact set of ![]() and denote by
and denote by ![]() the complementary set of
the complementary set of![]() . Suppose that assumptions (A1)-(A6) are satisfied and:
. Suppose that assumptions (A1)-(A6) are satisfied and:
(1) ![]()
(2)![]() ,
, ![]() and
and ![]() are such that
are such that ![]() and
and
![]()
(3) ![]()
(4) ![]()
(5) ![]()
then
![]()
The proof can be found in the Appendix.
Remark 2. Let ![]() a compact set of
a compact set of ![]() where
where ![]() is a sequence of positive
is a sequence of positive
numbers diverging to infinity. Let![]() ,
, ![]() and
and![]() ,
, ![]() , then the two dimensional stochastic process with invariant density
, then the two dimensional stochastic process with invariant density![]() ,
, ![]() ,
, ![]()
where![]() , satisfies the conditions of Lemma 2.
, satisfies the conditions of Lemma 2.
Theorem 4. (asymptotic normality)
Under assumption (A7) and conditions of Lemma 1 and Lemma 2, if
(1) for all![]() ,
, ![]() is twice continuously differentiable at
is twice continuously differentiable at![]() ,
,
(2) the components of ![]() and
and ![]() belong to
belong to ![]() and if the norms of these components are continuous functions at
and if the norms of these components are continuous functions at![]() ,
,
(3) ![]() is in the interior of
is in the interior of ![]() and
and ![]() is a non-singular matrix, then the limiting distribution of
is a non-singular matrix, then the limiting distribution of ![]() is
is ![]() where
where
![]()
Proof. From Theorem 2 [7] , we have:
![]()
where ![]() is a (m ´ m) matrix which tends to 0 as
is a (m ´ m) matrix which tends to 0 as![]() .
.
We have
![]()
Denote
![]()
We have
![]()
where
![]()
By Lemma 2, ![]() in probability as
in probability as![]() ; then, the limiting distribution of
; then, the limiting distribution of ![]() is reduced to that of
is reduced to that of
![]()
since![]() . But
. But
![]()
Therefore the limiting distribution of
![]()
where
![]()
This completes the proof of the theorem.
4. Examples and Simulations
4.1. Example 1
We consider the two-dimensional Ornstein-Uhlenbeck process solution of the stochastic differential equation
![]() (2)
(2)
where
![]()
Let ![]() and
and![]() , we have:
, we have:
![]()
![]() and
and ![]() satisfy assumptions (A1)-(A3). Therefore,
satisfy assumptions (A1)-(A3). Therefore, ![]() is exponentially strong mixing and the invariant distribution
is exponentially strong mixing and the invariant distribution ![]() admits a density
admits a density ![]() with respect to the Lebesgue measure.
with respect to the Lebesgue measure.
Furthermore [15] , ![]() , the Gaussian distribution on
, the Gaussian distribution on ![]() with
with ![]() the unique symmetric solution of the equation is
the unique symmetric solution of the equation is
![]() (3)
(3)
The solution of the Equation (3) is![]() .
.
Therefore [16] , the density of the invariant distribution is
![]()
The minimum Hellinger distance estimator of ![]() is defined by:
is defined by:
![]()
where
![]()
with
![]()
where ![]() is a kernel function which satisfies conditions (A4) and (A5) such that
is a kernel function which satisfies conditions (A4) and (A5) such that![]() .
.
Let![]() , we can write Equation (2) as follows:
, we can write Equation (2) as follows:
![]()
which gives the the following system
![]()
Thus, ![]() and
and ![]() are two independent univariate Ornstein-Uhlenbeck processes of parameters
are two independent univariate Ornstein-Uhlenbeck processes of parameters ![]() and
and ![]() respectively.
respectively.
We now give simulations for different parameter values using the R language. For each process, we generate sample paths using the package “sde” [17] and to compute a value of the estimator, we use the function “nlm” [18] of the R language. The kernel function ![]() is the density of the standard normal distribution. We use the
is the density of the standard normal distribution. We use the
bandwidth ![]() according to conditions on the bandwidth in the paper.
according to conditions on the bandwidth in the paper.
Simulations are based on 1000 observations of the Ornstein-Uhlenbeck process with 200 replications.
Simulation results are given in the Table 1.
![]()
Table 1. Means and standard errors of the minimum Hellinger distance estimator.
In Table 1, ![]() denotes the true value of the parameter and
denotes the true value of the parameter and ![]() denotes an estimation of
denotes an estimation of ![]() given by the minimum Hellinger distance estimator. Simulation results illustrate the good properties of the estimator. Indeed, the means of the estimator are quite close to the true values of the parameter in all cases and the standard errors are low.
given by the minimum Hellinger distance estimator. Simulation results illustrate the good properties of the estimator. Indeed, the means of the estimator are quite close to the true values of the parameter in all cases and the standard errors are low.
4.2. Example 2
We consider the Homogeneous Gaussian diffusion process [19] solution of the stochastic differential equation
![]() (4)
(4)
where ![]() is known, W is a two-dimensional Brownian motion, B is a
is known, W is a two-dimensional Brownian motion, B is a ![]() matrix with eigenvalues with strictly negative parts and A is a
matrix with eigenvalues with strictly negative parts and A is a ![]() matrix. By condition on the matrix B, X has an invariant probability
matrix. By condition on the matrix B, X has an invariant probability ![]() where
where ![]() and
and ![]() is the unique symetric solution of the equation
is the unique symetric solution of the equation
![]() (5)
(5)
Let
![]()
As in [19] , we suppose that![]() . In the following, we suppose that
. In the following, we suppose that![]() .
.
Then we have
![]()
Let![]() , we have
, we have![]() .
.
![]()
![]()
Let ![]() and
and![]() , we have
, we have![]() ;
; ![]() is invertible and we have
is invertible and we have
![]()
![]() is invertible and we have
is invertible and we have![]() . Hence, the invariant density of
. Hence, the invariant density of ![]() is
is
![]()
Table 2. Means and standard errors of the estimators.
![]()
For simulation, we must write the stochastic differential Equation (4) in matrix form as follows:
![]()
As in [19] , the true values of the parameter ![]() are
are ![]() and
and![]() . Then, we have
. Then, we have
![]()
Now, we can simulate a sample path of the Homogeneous Gaussian diffusion using the “yuima” package of R language [20] . We use the function “nlm” to compute a value of the estimator.
We generate 500 sample paths of the process, each of size 500. The kernel function and the bandwidth are those of the previous example.
We compare the estimator obtained by the minimum Hellinger distance method (MHD) of this paper and the estimator obtained in [19] by estimating function. Table 2 summarizes results of simulation of means and standard errors of the different estimators.
Table 2 shows that the two estimators have good behavior. For the two methods, the means of the estimators are close to the true values of the parameter. But the standard errors of the MHD estimator are lower than those of the estimating function estimator.
Appendix
A1. Proof of Theorem 1
Proof.
![]()
We have:
Step 1:
![]()
by Theorem 2.1 [21] .
Hence
![]() (6)
(6)
Step 2:
![]()
where
![]()
![]()
![]()
Then by theorem 2.1 [9] , we have for all ![]()
![]()
We have
![]()
where
![]()
Then
![]()
Therefore
![]() (7)
(7)
by the Borel-Cantelli’s lemma.
(6) and (7) imply that
![]()
This achieves the proof of the theorem.
A2. Proof of Theorem 2
Proof.
![]()
(1)
By making the change of variable ![]() and using assumptions (A4) and (A5), we get:
and using assumptions (A4) and (A5), we get:
![]()
(2)
![]()
where
![]()
We have ![]() and
and![]() .
.
Let![]() ,
, ![]() and
and ![]() be positive integers which tend to infinity as
be positive integers which tend to infinity as ![]() such that
such that![]() .
.
Define ![]() and
and ![]() by
by
![]()
and
![]()
We have
![]()
Step 1: We prove that ![]() in probability.
in probability.
By Minkowski’s inequality, we have
![]()
(1) Using Billingsley’s inequality [22] ,
![]()
(2)
![]()
Hence,
![]()
Therefore, choosing ![]() and
and ![]() such that
such that
![]() (8)
(8)
we get
![]()
which implies that
![]()
Step 2: asymptotic normality of![]() .
.
![]() ,
, ![]() have the same distribution; so that
have the same distribution; so that
![]()
From Lemma 4.2 [23] , we have
![]()
Setting![]() . If
. If ![]() and
and ![]() are chosen such that
are chosen such that
![]() (9)
(9)
the charasteristic function of ![]() is
is ![]() which is the charasteristic function of
which is the charasteristic function of ![]() where
where![]() ,
, ![]() are independent random variables with distribution that of
are independent random variables with distribution that of![]() .
.
We have ![]() and
and
![]()
(1) ![]()
(2) Note that ![]() with
with![]() .
.
![]() (10)
(10)
Therefore
![]()
Since the random variables ![]() have the same distribution, then by Lyapunov’s theorem [24] ,
have the same distribution, then by Lyapunov’s theorem [24] ,
the limiting distribution of ![]() is
is ![]() where
where
![]()
The condition (8), (9) and (10) are satisfied, for example, with
![]()
This achieves the proof of the theorem.
A3. Proof of Lemma 1
Proof. The proof of the lemma is done in two steps.
Step 1: we prove that
![]()
![]()
With assumptions (A4) and (A5), we have
![]()
Furthermore,
![]()
Therefore
![]()
Step 2: asymptotic normality of![]() ,
, ![]() ,
, ![]()
(1) ![]()
Proof is similar to that of theorem 2; we use the inequality of Davidov [22] instead of that of Billingsley.
Note that:
![]()
and
![]()
(2)![]() ,
, ![]()
Recall that ![]() if and only if
if and only if ![]() for all
for all![]() .
.
Let![]() ,
, ![]() and
and![]() , the real random variables
, the real random variables ![]() are
are
strongly mixing with mean zero and variance ![]() where
where ![]() is the covariance matrix of
is the covariance matrix of![]() ;
;![]() .
.
From (1),![]() .
.
Therefore,
![]()
This completes the proof of the lemma.
A4. Proof of Lemma 2
Proof.
![]()
We have,
![]()
Now,
![]()
(1)
![]()
Using Davidov’s inequality for mixing processes, we get
![]()
Choose ![]() and
and![]() , we obtain
, we obtain
![]()
Hence,
![]()
(2)
![]()
Therefore,
![]()
The last relation implies that
![]() (11)
(11)
Furthermore,
![]()
We have,
![]()
Therefore, if
![]()
then
![]() (12)
(12)
(11) and (12) imply that
![]()