Fluctuation-Model-Based Discrete Probability Estimation for Small Samples ()
1. Introduction
For categorical observational data analysis, it is often necessary to deal with multivariate systems since variables of such data generally depend on each other. Highly predictive statistical inference requires parameters that achieve low-entropy, so it is preferable to use data of many variables because the following relationship in Shannon entropies H of random variables X and Y holds if X and Y depend on each other: 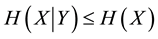 [1] , where
[1] , where 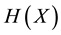 denotes Shannon entropy of X and
denotes Shannon entropy of X and 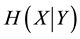 denotes the conditional entropy of X given Y. These are respectively defined with marginal, joint, and conditional probability mass functions P as follows [1] :
denotes the conditional entropy of X given Y. These are respectively defined with marginal, joint, and conditional probability mass functions P as follows [1] :
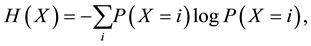
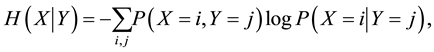
where i and j are indices of discrete states of X and Y. When we estimate probabilities in discrete probabilistic models with many-variables (e.g., Markov network and Bayesian network models [2] ), statistical estimation of conditional and joint probabilities often needs exponentially large data because of the combinatorial explosion of binding events in variables. Therefore, the models are often inferred from insufficient data. The maximum likelihood (ML) method provides an estimated probability function, which of X with k discrete states is expressed by
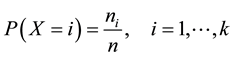
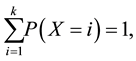
where n and 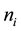 respectively denote a sample size and the frequency of occurrences in i state. The estimated probability is correct in the large sample limit. However, the ML methods suffer from short size data, and few robust methods have been investigated for such data in estimation of discrete probability functions as far as we know, although many robust methods for outliers such as M-estimators have been developed [3] [4] in para- metric continuous distributions. The maximum entropy method [5] , which may be applied to small datasets, was originally appropriate for data with missing information.
respectively denote a sample size and the frequency of occurrences in i state. The estimated probability is correct in the large sample limit. However, the ML methods suffer from short size data, and few robust methods have been investigated for such data in estimation of discrete probability functions as far as we know, although many robust methods for outliers such as M-estimators have been developed [3] [4] in para- metric continuous distributions. The maximum entropy method [5] , which may be applied to small datasets, was originally appropriate for data with missing information.
In the present study, a new robust method is proposed for estimating discrete probability functions for small samples. The method uses a parameterized objective function based on Kullback-Leibler divergence [6] and Shannon entropy. The function has a similar form to the Helmholtz free energy function that appears in statistical physics [7] [8] . A key feature of the method is a model of the parameter that controls the trade-off between likelihood and robustness in response to the degree of data fluctuation. The method thus does not require the value of the parameter to be manually selected. This model is a modification of a preceding work [9] , in which the parameter is represented by an artificial model containing a free hyperparameter.
In the domain of machine learning, although several methods slightly similar to ours have been proposed [10] - [14] , there is a critical distinction between these methods and ours. Many studies that have applied free energy to statistical inference have not included the similar trade-off parameter or have treated it as a fixed value, a manually controlled parameter, or a free parameter. Regarding the existing methods, we thus consider that the potentials of free-energy-like functions have not been well extracted. Other similar methods have been developed in the context of robust estimation for outliers, in which a free parameter is introduced in an analogous fashion [3] [15] [16] . However, the problem of how to determine the value of the free parameters remains.
This paper is organized as follows. In the next section, an objective function with parameter 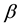 is introduced for robust estimation, and then probability functions obtained by the proposed method are shown to be formally equivalent to the canonical distributions that appear in statistical physics. In Section 3, a new representation of
is introduced for robust estimation, and then probability functions obtained by the proposed method are shown to be formally equivalent to the canonical distributions that appear in statistical physics. In Section 3, a new representation of 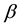 is presented as a data-fluctuation-model, and the preferable asymptotic property of
is presented as a data-fluctuation-model, and the preferable asymptotic property of 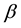 is proved. In Section 4, some characteristic properties among quantities used in the proposed method are provided. In Section 5, we perform experiments using the proposed probability estimation method. In Section 6, conclusions regarding the estimation method are given.
is proved. In Section 4, some characteristic properties among quantities used in the proposed method are provided. In Section 5, we perform experiments using the proposed probability estimation method. In Section 6, conclusions regarding the estimation method are given.
2. Probability Estimation with Parameter β
Note that in this paper a capital letter (such as X) denotes a random discrete variable, a non-capital letter (such as x) denotes the special state of that variable, a bold capital letter (such as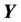 ) denotes a set of variables, and a bold non-capital letter (such as
) denotes a set of variables, and a bold non-capital letter (such as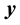 ) denotes configurations of that set.
) denotes configurations of that set.
To construct a method for estimating finite-discrete-probability distributions of random variable X from sample set of finite size n, the following quantities are defined. 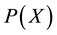 denotes a discrete-probability function estimated by a proposed method that is described below. A function of X is defined as
denotes a discrete-probability function estimated by a proposed method that is described below. A function of X is defined as 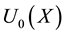 on the basis of the Kullback--Leibler (KL) divergence [6] between empirical functions and
on the basis of the Kullback--Leibler (KL) divergence [6] between empirical functions and 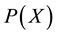 as follows:
as follows:
![]() (1)
(1)
where ![]() is a empirical distribution function. For non-parametric discrete distributions, the empirical distributions are equivalent to relative frequencies; i.e., they are equivalent to the maximum likelihood (ML) dis- tributions.
is a empirical distribution function. For non-parametric discrete distributions, the empirical distributions are equivalent to relative frequencies; i.e., they are equivalent to the maximum likelihood (ML) dis- tributions. ![]() can thus be replaced by ML distributions denoted by
can thus be replaced by ML distributions denoted by![]() . An objective function
. An objective function ![]() is defined as follows:
is defined as follows:
![]() (2)
(2)
where ![]() is defined by Equation (1),
is defined by Equation (1), ![]() is the Shannon entropy [1] of the estimated functions given
is the Shannon entropy [1] of the estimated functions given
as![]() , and
, and ![]() is a parameter that is defined so that
is a parameter that is defined so that![]() .
. ![]()
and ![]() are introduced for later convenience.
are introduced for later convenience. ![]() is represented by a cross entropy
is represented by a cross entropy ![]() and
and ![]() is a normalization parameter of
is a normalization parameter of ![]() as follow:
as follow:
![]() (3)
(3)
and
![]() (4)
(4)
where![]() .
. ![]() can be rewritten by using
can be rewritten by using ![]() and
and ![]() as:
as:
![]() (5)
(5)
In addition, the following quantity ![]() is defined as
is defined as
![]() (6)
(6)
![]() is also written with
is also written with ![]() as
as![]() ; that is,
; that is, ![]() denotes an expectation value in respect to
denotes an expectation value in respect to![]() .
.
The estimator of probability functions, ![]() , is defined so as to minimize Lagrangian L consisting of
, is defined so as to minimize Lagrangian L consisting of ![]() as
as![]() . L is expressed as
. L is expressed as
![]() (7)
(7)
where ![]() is the Lagrange multiplier.
is the Lagrange multiplier. ![]() is thereby obtained as
is thereby obtained as
![]() (8)
(8)
where ![]() as expressed in Equation (6) is used. Equation (8) is equivalent to a form known as the canonical distribution, which is also called Gibbs distribution, in statistical physics. The following equivalent form is more convenient for practical use:
as expressed in Equation (6) is used. Equation (8) is equivalent to a form known as the canonical distribution, which is also called Gibbs distribution, in statistical physics. The following equivalent form is more convenient for practical use:
![]() (9)
(9)
For estimating conditional and joint-probability functions, conditional entropy![]() , which is defined as:
, which is defined as:![]() , and conditional KL divergence:
, and conditional KL divergence:
![]()
are used. ![]() for
for ![]() is defined as
is defined as
![]()
The formula for estimating conditional probabilities is therefore obtained by using the conditional entropy and KL divergence and ![]() in the following form:
in the following form:
![]() (10)
(10)
Joint probability can be calculated by using Equations (8) and (10) and the definite relation ![]() . In general, it is calculated using decomposition rules such that
. In general, it is calculated using decomposition rules such that
![]()
3. Model of β
![]() approaches
approaches ![]() when
when ![]() in Equation (9) approaches 1. On the other hand,
in Equation (9) approaches 1. On the other hand, ![]() approaches the uniform distribution if
approaches the uniform distribution if ![]() and
and ![]() approaches 0. If
approaches 0. If ![]() close to 1 represents that the data size is suffi- ciently large and if
close to 1 represents that the data size is suffi- ciently large and if ![]() close to 0 represents that the data size is very small,
close to 0 represents that the data size is very small, ![]() has favorable properties for accurate and robust estimation. This is because the ML estimators generally have preferable consistency and asymptotic efficiency and the distributions close to the uniform can be regarded as the ones that have robustness for small size data. Before
has favorable properties for accurate and robust estimation. This is because the ML estimators generally have preferable consistency and asymptotic efficiency and the distributions close to the uniform can be regarded as the ones that have robustness for small size data. Before ![]() is defined, the following quantity
is defined, the following quantity ![]() with n data size is defined by a geometric mean as
with n data size is defined by a geometric mean as
![]() (11)
(11)
where ![]() denotes a normalization constant, and
denotes a normalization constant, and ![]() denotes the estimated function obtained from Equation (9) with initial i data. It is defined that
denotes the estimated function obtained from Equation (9) with initial i data. It is defined that![]() , where
, where ![]() denotes the number of states of variable X. Fluctuation
denotes the number of states of variable X. Fluctuation ![]() of X with n data is given as
of X with n data is given as
![]()
Then, ![]() for n data is defined by using an expectation value of
for n data is defined by using an expectation value of ![]() with respect to
with respect to![]() , i.e., the following KL divergence:
, i.e., the following KL divergence:
![]() (12)
(12)
where![]() , and
, and ![]() is the ML estimator function obtained from n data. It is assumed that
is the ML estimator function obtained from n data. It is assumed that
![]() . The normalized
. The normalized![]() , that is,
, that is, ![]() , is defined by Equation (4). Note that the canonical
, is defined by Equation (4). Note that the canonical
distribution ![]() expressed by Equation (9) can be determined, without any free parameters, by using Equations (9), (11), (12), (4), and
expressed by Equation (9) can be determined, without any free parameters, by using Equations (9), (11), (12), (4), and ![]() for data size
for data size![]() . It is also defined that in Equation (10) for conditional data size
. It is also defined that in Equation (10) for conditional data size ![]() given
given![]() ,
, ![]() for any
for any ![]() in the same manner as
in the same manner as![]() .
.
Objective function F is rewritten in the same form as that in statistical mechanics as follows:
![]() (13)
(13)
where Z is the partition function, which is a similar function well known in statistical mechanics, defined for single or multivariate probabilities as
![]() (14)
(14)
and for conditional probabilities as
![]() (15)
(15)
A significant feature of ![]() is confirmed as follows. The lemma needed for this proof is stated as
is confirmed as follows. The lemma needed for this proof is stated as
Lemma 1.
![]() is denoted as the canonical distribution estimated from Equation (8) with i data. For data size
is denoted as the canonical distribution estimated from Equation (8) with i data. For data size![]() ,
, ![]() , defined by Equation (11), converges to a definite value
, defined by Equation (11), converges to a definite value ![]() when
when ![]() for inte- gers i such that
for inte- gers i such that ![]() and any state x of X.
and any state x of X.
Proof.
![]() (16)
(16)
Because ![]() and
and![]() ,
, ![]() and
and ![]() are definite values. Thus both terms on the right-hand side of Equation (16) converge to
are definite values. Thus both terms on the right-hand side of Equation (16) converge to![]() , which is a constant if
, which is a constant if![]() . Hence,
. Hence, ![]() , with constant b, can be written. Therefore,
, with constant b, can be written. Therefore, ![]() and
and ![]() in order that
in order that ![]() converges not to 0 or 1 but to definite values. □
converges not to 0 or 1 but to definite values. □
Theorem 1. At the asymptotic limit (i.e., large sample limit), ![]() converges to 1 when
converges to 1 when ![]() for integers i such that
for integers i such that ![]() and any state x, where
and any state x, where ![]() is denoted as the canonical distribution represented by Equation (8) from i data.
is denoted as the canonical distribution represented by Equation (8) from i data.
Proof. According to Lemma 1, ![]() at the limit
at the limit![]() , where
, where ![]() is a definite value for any x. The following Equation is thus obtained from Equation (11) with
is a definite value for any x. The following Equation is thus obtained from Equation (11) with ![]() as follows:
as follows:
![]() (17)
(17)
![]() thus converges to a definite value, and
thus converges to a definite value, and ![]() converges to
converges to ![]() (and the constant in Equation (17) goes to 0) at
(and the constant in Equation (17) goes to 0) at![]() . Meanwhile, ML estimator
. Meanwhile, ML estimator ![]() converges to true distribution
converges to true distribution ![]() due to the consistency of the ML estimators, and
due to the consistency of the ML estimators, and ![]() thus converges to a definite value according to Equation (9).
thus converges to a definite value according to Equation (9). ![]() at
at ![]() is denoted as
is denoted as![]() . Therefore, the following Equation is derived from Equations (4), (9) and (12) at
. Therefore, the following Equation is derived from Equations (4), (9) and (12) at![]() ,
,
![]() (18)
(18)
for ![]() and any state
and any state![]() . Equation (18) requires
. Equation (18) requires ![]() or
or ![]() in order that
in order that ![]() or
or
![]() is a constant for any probability distribution
is a constant for any probability distribution![]() . However,
. However, ![]() does not satisfy Equation
does not satisfy Equation
(18), while ![]() satisfies it. Accordingly,
satisfies it. Accordingly, ![]() at the asymptotic limit. □
at the asymptotic limit. □
According to Theorem 1, the more data are obtained, the more ![]() approaches 1, and the more the estimator approaches the ML estimator. The estimator that is obtained by the proposed method therefore has the same preferable asymptotic properties, namely, consistency and efficiency, as the ML estimators have. For insuffi- cient data size,
approaches 1, and the more the estimator approaches the ML estimator. The estimator that is obtained by the proposed method therefore has the same preferable asymptotic properties, namely, consistency and efficiency, as the ML estimators have. For insuffi- cient data size, ![]() is probably small due to the influence of the uniform distributions given by Equation (12), so
is probably small due to the influence of the uniform distributions given by Equation (12), so ![]() is also small. The estimated probability functions by the proposed method are thus interpreted as adap- tively tempered ML estimator functions in response to the degree of data fluctuation. The proposed estimation method does thereby not require manually selecting the value of parameter
is also small. The estimated probability functions by the proposed method are thus interpreted as adap- tively tempered ML estimator functions in response to the degree of data fluctuation. The proposed estimation method does thereby not require manually selecting the value of parameter![]() , and is called “ATML,” which is abbreviated as the “adaptively tempered ML” method. ATML has an advantage of simpleness over methods that need complicated algorithms (e.g., [17] ).
, and is called “ATML,” which is abbreviated as the “adaptively tempered ML” method. ATML has an advantage of simpleness over methods that need complicated algorithms (e.g., [17] ).
The role of ![]() can be seen as a trade-off parameter between likelihood and robustness by referring to another expression of Equation (2) as follows:
can be seen as a trade-off parameter between likelihood and robustness by referring to another expression of Equation (2) as follows:
![]() (19)
(19)
where ![]() denotes the uniform distribution function, which contributes to the robustness, while
denotes the uniform distribution function, which contributes to the robustness, while ![]() contributes to the likelihood. Additionally, objective function F can also be interpreted as a KL-based diver- gence measure since
contributes to the likelihood. Additionally, objective function F can also be interpreted as a KL-based diver- gence measure since ![]() is also represented by a KL divergence.
is also represented by a KL divergence.
ATML has an analogy with statistical physics, since the canonical distribution for the estimator is obtained from Equation (8). Actually, U, H, ![]() , and F respectively play similar roles to (internal) energy, entropy, (inverted) temperature, and Helmholtz free energy in statistical physics. Solving Equation
, and F respectively play similar roles to (internal) energy, entropy, (inverted) temperature, and Helmholtz free energy in statistical physics. Solving Equation ![]() for obtaining
for obtaining ![]() mathematically corresponds to employing the minimum-free-energy (MFE) principle [7] in thermal physics.
mathematically corresponds to employing the minimum-free-energy (MFE) principle [7] in thermal physics.
ATML may seem analogous to Jaynes’ maximum entropy (ME) methods [5] , which are well known as least- biased inference methods. However, the constraints on which ME methods are based may not be reliable for small samples and thus may be biased, although this kind of bias is not usually considered. On the other hand, ATML is thus designed so that even the bias can be corrected by using parameter![]() .
.
4. Characteristic Properties of ATML
The canonical distribution expressed as Equation (8) can provide some characteristic properties of ATML, which are similar to those in statistical physics. The following notations are defined for later convenience. Pro- bability mass functions that are estimated by ATML, denoted by![]() , have discrete states denoted as index k. The corresponding ML estimator is denoted by
, have discrete states denoted as index k. The corresponding ML estimator is denoted by![]() , and
, and ![]() is used instead of
is used instead of![]() .
.
In statistical physics, (inverted) temperature ![]() is usually defined as [7] [8]
is usually defined as [7] [8]
![]() (20)
(20)
If the canonical distribution of![]() , which takes the form of Equation (8), is used, Equation (20) is auto- matically satisfied as follows:
, which takes the form of Equation (8), is used, Equation (20) is auto- matically satisfied as follows:
Lemma 2. ![]() under the MFE condition, where H, U,
under the MFE condition, where H, U, ![]() , and Z are defined in the previous sections.
, and Z are defined in the previous sections.
Proof. Since probability mass function ![]() has a canonical form under the MFE condition, it follows that
has a canonical form under the MFE condition, it follows that
![]() (21) □
(21) □
Theorem 2. Equation (20) is automatically satisfied under the MFE condition.
Proof. Partially differentiating both sides of Equation (21) with respect to U gives
![]() (22)
(22)
![]() (23)
(23)
![]()
It follows that
![]() □
□
In the same way, it can be proved that![]() .
.
![]() , which is called energy fluctuations in statistical mechanics, is shown to have the following relation, where
, which is called energy fluctuations in statistical mechanics, is shown to have the following relation, where ![]() denotes an expectation value with respect to the canonical distributions.
denotes an expectation value with respect to the canonical distributions.
![]() (24)
(24)
In regard to ![]() defined in the proposed estimation method, namely, Equation (6), the same relation as that shown here is satisfied as follows:
defined in the proposed estimation method, namely, Equation (6), the same relation as that shown here is satisfied as follows:
![]()
Equation (24) is therefore proved.
Fisher information ![]() with a parameter
with a parameter ![]() is defined in the usual way as
is defined in the usual way as
![]() (25)
(25)
where f is the likelihood function. We define tempered Fisher information ![]() as Fisher information where the likelihood function is replaced with the canonical distributions with parameter
as Fisher information where the likelihood function is replaced with the canonical distributions with parameter![]() . It is shown that
. It is shown that ![]() as follows:
as follows:
![]() (26)
(26)
The tempered Fisher information is therefore identical to Equation (24).
It is noteworthy that ATML has other mathematical similarities with statistical physics. That is, the same relationships that appear in statistical physics listed as follows hold.
・ The following relation is easily derived from the definition of partition function Z:
![]() (27)
(27)
・ The following relation, known as the Gibbs-Helmholtz relation, is derived from Equations (13) and (27) as
![]() (28)
(28)
・ The following relation is simply obtained from Equations (5) and (28) as
![]() (29)
(29)
・ The tempered Fisher information is represented by the second-order differential of the partition function for ![]() as
as
![]() (30)
(30)
5. Examples
Numerical experiments are performed to demonstrate the robustness of ATML for small samples, in comparison with the ML and ME methods [5] .
X is assumed to have three internal states and four probability mass functions with a variety of entropies denoted as ![]() in natural logarithms as
in natural logarithms as
1.![]() ,
,
2.![]() ,
,
3.![]() ,
,
4.![]() .
.
Data from each function was sampled, and probabilities were estimated from given data sets with various data sizes. According to convention, averaged outputs ![]() were set as the constraint in the ME method as follows:
were set as the constraint in the ME method as follows:
![]() , where Xd denotes d-th sample’s output, and N denotes sample size. After that, true and
, where Xd denotes d-th sample’s output, and N denotes sample size. After that, true and
estimated probabilities were compared by using KL divergence as a metric with the following form:
![]() (31)
(31)
where ![]() is the true distribution, and
is the true distribution, and ![]() is the distribution estimated by ML, ME, or ATML. For avoiding zero probabilities, probabilities were smoothed by adding 0.0001 to the counts.
is the distribution estimated by ML, ME, or ATML. For avoiding zero probabilities, probabilities were smoothed by adding 0.0001 to the counts.
The KL divergences are shown in Figure 1, where they are averaged values from 100 samples at each sample size from identical distributions. It can be seen that the ML estimators are inferior to ATML due to overfitting, except for the distribution having very small entropy. Even the degree of superiority of the ML estimation in (d) is relatively smaller than that of inferiority in other distributions. The ME estimators showed the opposite be- haviors to those by the ML estimators, and showed some relatively poor results in large-sample regions. ML methods tend to fit data and can thus more accurately estimate distributions with very low entropies than others in small-sample cases. For example, if a true entropy equals zero, the ML method can estimate the exact true
![]()
Figure 1. KL divergences between true probability mass functions and probability mass functions estimated by using ML, ATML, and ME. The horizontal axes denote sample sizes. H denotes Shannon entropy in natural logarithms. (a) H = 1:07; (b) H = 0:841; (c) H = 0:498; (d) H = 0:0621.
distribution from only one sample. On the other hand, ME methods tend to increase entropies and can thereby accurately estimate distributions with high entropies close to the uniform distributions. Hence, the ML method tends to overfit data, and the ME method tends to underfit data in the view of misestimation. Even so, ATML showed relative stability in terms of both sample sizes and distributions. This result indicates the effectiveness of ATML as a probability estimation method.
6. Conclusion
A robust method for estimating discrete probability functions, called “adaptively tempered maximum likelihood” method (ATML for short), is proposed. The estimators obtained in this method minimize a parameterized objective function similar to Helmholtz free energies that appear in statistical physics. The key feature of the proposed method is a model of the parameter as a fluctuation of finite size data. The parameter that is modeled plays an important role in determining the appropriate trade-off between likelihood and robustness in response to the degree of the fluctuations. ATML does thereby not require manually selecting the value of the parameter. It is also proved that the obtained estimator approaches the maximum likelihood estimator at the asymptotic limit. The effectiveness of ATML in terms of robustness was demonstrated by experimental studies on point estimation for probability distributions with various entropies.
Acknowledgements
The author thanks Mario Tokoro and Hiroaki Kitano of Sony Computer Science Laboratories, Inc. for their support as well as Te Sun Han, Hiroshi Nagaoka, Tomohiro Ogawa and Jun Suzuki of the University of Electro- Communications for their valuable comments and discussions.