Fuzzy Logic Approach for Solving an Optimal Control Problem of an Uninfected Hepatitis B Virus Dynamics ()
1. Introduction
Hepatitis B is one of various diseases that are potentially life-threatening liver infection. Abbreviated in terms of HBV [1] , hepatitis B virus is a species of the genus Orthohepadna virus that is found in Hepadnaviridae family viruses. For some cases, HBV results in serious liver diseases such as chronic hepatic insufficiency, hepatocellular carcinoma, cirrhosis and can be a potential cause of the liver cancer [2] . For instance, the commonly worldwide well-known Hepatocellular carcinoma (HCC) is a cancer and more than half of HCC patients are attributable to persistent HBV infections. It is approximated that between 15% and 40% of infected patients develop cirrhosis, liver failure, or HCC which occupies the fifth place of the most frequent dangerous cancers, killing 300,000 - 500,000 each year. Taking in account of the HBV danger, its prevention is made up throughout the universal hepatitis B vaccination program, which currently is leading to a tangible reduction of incidence rates of childhood HCC in several countries. However, this is not a 100% answer to that health change because there are still hundreds of millions of people suffering HBV today. In the past decade, several hepatitis B viral factors such as serum HBV DNA level, genotype, and naturally occurring mutants have already been identified to influence liver disease progression [3] .
It has been scientifically found that hepatitis B is transmitted through contact with blood or bodily fluids from an individual infected with the hepatitis B virus (HBV). The virus mainly affects liver function; this is, it invades the liver cells (hepatocytes) and uses the cells’ machinery to replicate within it. The hepatitis B virion binds to the hepatocyte via the domain of the viral surface antigen. The cell then engulfs the virus in a process called endocytosis. As the infection occurs, the host immune response is triggered. The body’s immune system attacks the infected hepatocytes, which lead to liver injury at the same time as clearing the virus from the body. The liver damage associated with HBV infection is mainly caused by the adaptive immune response, particularly the virus-specific cytotoxic T lymphocytes (CTLs). These CTLs kill cells that contain the virus. Liver damage is also aggravated by the antigen-nonspecific inflammatory cells and activated platelets at the site of infection.
There are two possible phases of this infection [2] :
1) Acute hepatitis B infection that lasts less than six months. In this case the immune system is usually able to clear the virus from the body, and the patient should recover completely within a few months. This kind of phase is the most case for adult people who acquire hepatitis B.
2) Chronic hepatitis B infection which lasts six months or longer. This infection manifests in the most infants infected with HBV at birth and many children infected between 1 and 6 years of age become chronically infected.
The chronic carrier people do not develop symptoms; these are taken as two-thirds of people with chronic HBV infection. In the all world more than 240 million people have chronic liver infections and about 600,000 people die every year due to the acute or chronic consequences of hepatitis B [2] .
Mathematical models can be a useful tool in controlling hepatitis B virus in order to put down the infection from the population. It is in the manner that the simple mathematical model has been used by Anderson and May to illustrate the effects of carriers on the transmission of HBV [4] . To develop a strategy for eliminating HBV in New Zealand [5] [6] , the mathematical model has been used by Medley et al [7] . An age structure model to predict the dynamics of HBV transmission and evaluate the long-term effectiveness of the vaccination program in China has been proposed by Zhao et al. [8] . The mathematical model developed by Pang et al. [9] allowed him to explore the impact of vaccination and other controlling measures of HBV infection while Bhattacharyya and Ghosh [10] , Kar and Batabyal [11] , and Kar and Jana [12] proposed optimal control of infectious diseases.
Several drug therapies have been proposed for treating persons with chronic HBV including adefovir dipivoxil, alpha-interferon, lamivudine, pegylated interferon, entecavir, telbivudine, and tenofovir [13] . Hepatitis antiviral drugs prevent replication of HBVs and save the liver from cirrhosis and cancer. During the treatment, the viral load is reduced and consequently the viral replication in liver is decreased [14] .
Optimal control theory has found wide-ranging applications in biological and ecological problems [15] . In biomedical problems, techniques from control theory are of great use in developing optimal therapeutic strategies. The treatment regimen is usually taken to be the control variable, with the aim of minimizing the detrimental effects of the medical condition. Optimal control theory can be used to optimize the drug doses required in the treatment of HBV infected patients [13] [16] [17] . The optimal treatment schedules for HBV have been designed using model predictive control (MPC) method [18] . One of the numerical methods for solving optimal control problem is fuzzy logic strategy [19] - [21] .
In this paper, the optimal control problem is presented and fuzzy logic strategy is used to solve it. It is organized as follows. Section 2 presents the model equations and optimal control problem. A short description of by fuzzy logic for solving optimal control problems is discussed in this section. Section 3 is interested in the application of the direct approach and the approach that integrates the fuzzy logic for solving an optimal control problem of an infected hepatitis B virus dynamics. The numerical simulation is presented in Section 4. Finally, we present concluding remarks in the last section.
2. Methods
2.1. Setting of the Problem
In terms of constraints of our problem, the option was put on the model proposed in [22] that incorporates the effect of two types of antiviral drugs as in [18] .
 (1)
(1)
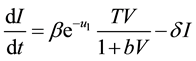 (2)
(2)
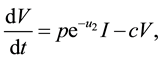 (3)
(3)
where T, I and V stand for the concentration of uninfected hepatocytes, infected hepatocytes and free virions respectively. In this context uninfected hepatocytes are produced at the constant rate s and die at the rate qT. For the purpose of describing the proliferation of existing T cells, we used the logistic function where a stands for the maximum proliferation rate of target cells and 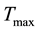 is the T concentration at which proliferation shuts off. The rate of infection is given by saturation functional response
is the T concentration at which proliferation shuts off. The rate of infection is given by saturation functional response 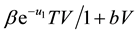 where
where  denotes the infection rate constant which characterizes the infection efficiency and where b is positive constant. The death rate of infected hepatocytes is given by
denotes the infection rate constant which characterizes the infection efficiency and where b is positive constant. The death rate of infected hepatocytes is given by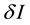 . The free virions are produced from infected hepatocytes at the rate of
. The free virions are produced from infected hepatocytes at the rate of 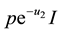 and
and  is the clearance rate of viral particles. In this model two types of drugs are taken. The first is described by chemotherapy functions
is the clearance rate of viral particles. In this model two types of drugs are taken. The first is described by chemotherapy functions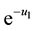 . It helps to prevent the virus from infecting the cell and the second facilitates the prevention of the infected cells from producing the new viruses; it is denoted by the function
. It helps to prevent the virus from infecting the cell and the second facilitates the prevention of the infected cells from producing the new viruses; it is denoted by the function .
.
If  is a state vector, then the healthy improvement conditions for an uninfected human should look for reaching uninfected steady state
is a state vector, then the healthy improvement conditions for an uninfected human should look for reaching uninfected steady state 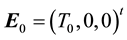 where
where 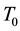 is the constant that must be found out. Next the cost function (objective function) was formulated in the following way.
is the constant that must be found out. Next the cost function (objective function) was formulated in the following way.
Find 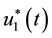 and
and 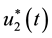 solution of
solution of
![]() (4)
(4)
subject to the system (1)-(3).
The positive scalar coefficients![]() ,
, ![]() and
and ![]() determine how much weight is attached to each cost com- ponent term in the integrand whereas
determine how much weight is attached to each cost com- ponent term in the integrand whereas ![]() denotes the maximum time that the physical activity can take.
denotes the maximum time that the physical activity can take.
Let’s ![]() be the vector space that is span of a base of linear B-splines function on a regular grid
be the vector space that is span of a base of linear B-splines function on a regular grid
![]() (5)
(5)
![]() (6)
(6)
The functions![]() ,
, ![]() satisfy the following relation
satisfy the following relation
![]()
where ![]() denotes Kronecker symbol.
denotes Kronecker symbol.
2.2. Description of Fuzzy Logic Approach
Let us consider the following problem.
Find![]() ,
, ![]() that minimizes
that minimizes
![]() (7)
(7)
subject to
![]() (8)
(8)
where ![]() and
and ![]() are positive defined matrices.
are positive defined matrices.
The problem (7)-(8) can be solved by the dynamic programming method. This method has a fast convergence, its convergence rate is quadratic and the optimal solution is often represented as a state of control feedback [23] . However, this method allows getting the solution which depends on the choice of the initial trajectory and in some cases that solution is not optimal. In this study we integrated fuzzy logic approach to achieve a guaranteed optimal solution [24] . We develop a linearization strategy of the subject system by an approach based on the fuzzy logic. This approach has been developed by Takagi-Sugeno [25] [26] and in1985 they carried out a model that can be used to find fuzzy linearization regions in the state [27] . Taking these fuzzy regions as basis, non linear system is decomposed in a structured multi models which is composed of several independent linear models [28] . The linearization is made around an operating point contained in these regions.
Let’s consider the set of operating points![]() ,
,![]() . Different fuzzy approximations of the nonlinear term
. Different fuzzy approximations of the nonlinear term ![]() can be considered.
can be considered.
1) The approximation of order zero gives:
![]() (9)
(9)
2) Using the first order of Taylor expansion series we obtain
![]() (10)
(10)
To improve this approximation, we introduced the factor of the consequence for fuzzy Takagi-Sugeno system. This factor allows to minimize the error between the non linear function and the fuzzy approximation. If ![]() designates this factor, the approximation (10) can be formulated as follows:
designates this factor, the approximation (10) can be formulated as follows:
![]() (11)
(11)
If one replaces the term nl by its value approached in (8), the linearization around ![]() leads to
leads to
![]() (12)
(12)
where ![]() and
and ![]() are square matrix which has
are square matrix which has ![]() order and
order and ![]() matrix with
matrix with ![]() order.
order.
Therefore, the optimal control problem (7)-(8) becomes a linear quadratic problem which the feedback control is given by the following expression [29] [30] :
![]() (13)
(13)
where
![]() (14)
(14)
is the feedback gain matrix and ![]() discrete Riccati equation solution of the following form
discrete Riccati equation solution of the following form
![]() (15)
(15)
Obviously the linearization around every operating point gives the system for which the equations have the form (12). Due to the presence of S operating points, S systems of that form should be formed and therefore according to the relation (13) S controls are determined. The defuzzyfication method [26] permits to determine only one system and only one control![]() .
.
Then, this transformation gives the following equation:
![]() (16)
(16)
![]() (17)
(17)
where
![]() (18)
(18)
and where ![]() designates membership degree partner to the operating point
designates membership degree partner to the operating point![]() .
.
3. Numerical Approaches for Solving the Optimal Control Problem (4), (1)-(3)
3.1. Using Fuzzy Logic Approach
To approximate the optimal control problem (4), (1)-(3), we propose to use the explicit Euler scheme because the stability of this scheme allows deal with some ordinary differential equations.
By letting the following variable change
![]() (19)
(19)
the system (1)-(3) becomes
![]()
The discretization of the constraints (1)-(3) is done using the first order explicit Euler method. The first order of explicit Euler’s method gives following system
![]() (20)
(20)
where![]() ,
,![]() .
.
Using the approximation ![]() the system (20) becomes
the system (20) becomes
![]()
that is
![]() (21)
(21)
Since the system (21) has nonlinear factors let us designate these points as![]() ,
, ![]() and
and![]() ,
, ![]() , for the first, second and third equation of the system (21) respectively. Obviously these points take the corresponding values in the labels centers of a universe of discourse X [24] .
, for the first, second and third equation of the system (21) respectively. Obviously these points take the corresponding values in the labels centers of a universe of discourse X [24] .
To simplify, we consider only the Taylor expansion of first order around the operating points![]() ,
, ![]() and
and![]() . We therefore obtain three systems of the following form
. We therefore obtain three systems of the following form
![]() (22)
(22)
Assuming that ![]() to be numbers related to each operating point, the system (22) can be written as follows
to be numbers related to each operating point, the system (22) can be written as follows
![]() (23)
(23)
where
![]() (24)
(24)
![]() (25)
(25)
and
![]() (26)
(26)
To approximate the objective function of the problem (4), we use the rectangular method. Hence, we obtain
![]() (27)
(27)
where![]() .
. ![]() and
and ![]() are the matrix
are the matrix
![]() (28)
(28)
Finally, the optimal control problem (4), (1)-(3) can be formulated as follows.
Find ![]() solution of
solution of
![]() (29)
(29)
subject to
![]() (30)
(30)
It easy to note that the problem (29)-(30) is a linear quadratic (LQ). Since there are three linear state systems, the solution leads to three feedback controls of the form
![]() (31)
(31)
where ![]() is a gain feedback.
is a gain feedback.
3.2. Using Direct Approach
To approximate the system (1)-(3), we consider
![]() (32)
(32)
a linear B-splines basis functions on the uniform grid
![]() (33)
(33)
such that
![]()
Let us introduce the vector space ![]() whose the basis is
whose the basis is![]() . We have
. We have
1) ![]()
2) ![]()
Let us consider ![]() and let us take the interpolation operator
and let us take the interpolation operator
![]() (34)
(34)
satisfying
![]() (35)
(35)
We verify easily that
![]() (36)
(36)
![]() (37)
(37)
Therefore, the system (1)-(3) can be approached by the following form.
Find ![]() solution of the system
solution of the system
![]() (38)
(38)
![]() (39)
(39)
![]() (40)
(40)
![]() (41)
(41)
such that
![]() (42)
(42)
![]() (43)
(43)
![]() (44)
(44)
The discretization of the optimal problem (4) is done as follows.
![]() (45)
(45)
where
![]() (46)
(46)
with ![]() and
and ![]() respectively the
respectively the ![]() component of the vectors
component of the vectors ![]() and
and ![]() respectively.
respectively.
We are looking for ![]() an approximated solution of (45) in the set
an approximated solution of (45) in the set ![]() such that
such that
![]()
Therefore the cost function (45) becomes
![]() (47)
(47)
where (47) is determined using rectangular method such that the discretization is done on a regular grid![]() .
.
The discrete formulation of optimal problem (4) subject to (1)-(3) is written as follows.
![]() (48)
(48)
where ![]() is a matrix
is a matrix ![]() such that the components
such that the components ![]() are components of the function
are components of the function ![]() in the set
in the set ![]() and
and ![]() represents the matrix with
represents the matrix with ![]() component,
component, ![]() denotes the first components of solution of the system (1)-(3) associated to
denotes the first components of solution of the system (1)-(3) associated to![]() ,
, ![]() and
and ![]() are matrix defined by
are matrix defined by
![]()
Finally, the optimal control problem (4), (1)-(3) is a minimisation problem with constraint. The discreet formulation of such problem can be written as follows.
Find ![]() solution of
solution of
![]() (49)
(49)
subject to
![]() (50)
(50)
where ![]() is a matrix
is a matrix ![]() such that the components
such that the components ![]() are those function
are those function ![]() in
in ![]() and
and ![]() is the matrix such that the
is the matrix such that the ![]() component is
component is ![]() where
where ![]() is the solution of (4), (1)-(3) associated to
is the solution of (4), (1)-(3) associated to![]() .
.
4. Numerical Simulation
Taking in account of the mechanism of linealisation of the nonlinear terms of the system (20), we applied the fuzzy approach where the concentration of uninfected hepatocytes for health person has been considered to be ![]() cells/dl. Furthermore, from optimal control problem (4), (1)-(3), the role of drugs of hepatitis B virus is to allow uninfected hepatocytes cells to be around the equilibrium value (T0 = 1000 cells/dl) and remove all infected hepatocytes (
cells/dl. Furthermore, from optimal control problem (4), (1)-(3), the role of drugs of hepatitis B virus is to allow uninfected hepatocytes cells to be around the equilibrium value (T0 = 1000 cells/dl) and remove all infected hepatocytes (![]() ) and virions (
) and virions (![]() ) in the body of patient. This is not quickly done but is a process during the time of administration of drugs by a patient. In this context x (universe of discourse) has two linguistic variables: uninfected hepatocytes (UH), infected hepatocytes (IH) and free virions (FV) respectively. Taking in account of the physiology, we consider
) in the body of patient. This is not quickly done but is a process during the time of administration of drugs by a patient. In this context x (universe of discourse) has two linguistic variables: uninfected hepatocytes (UH), infected hepatocytes (IH) and free virions (FV) respectively. Taking in account of the physiology, we consider ![]() and
and ![]() and
and![]() . Therefore, the uninfected hepatocyte, infected hepatocytes and free virions are low if
. Therefore, the uninfected hepatocyte, infected hepatocytes and free virions are low if ![]() cells/dl,
cells/dl, ![]() and
and ![]() respectively.
respectively.
If T, I and are respectively included in the middle of 200 and 1500 cells/dl, 0 and 300cells/dl and 0 and 500, we suppose that the concentration of uninfected hepatocytes (UH), infected hepatocytes (IH) and free virions (FV) are normal. While if![]() ,
, ![]() and
and ![]() we say that the uninfected hepatocytes, infected hepatocytes and free virions are the highest. Then, LUH (low uninfected hepatocytes), NUH (normal uninfected hepatocytes) and GUH (the highest uninfected hepatocytes) constitute the terms (fuzzy sets) of the linguistic variable UH. Similarly, LIH, NIH and GUH (respectively LFV, NFV and GFV are used for the terms of the variable linguistic IH (respectively FV).
we say that the uninfected hepatocytes, infected hepatocytes and free virions are the highest. Then, LUH (low uninfected hepatocytes), NUH (normal uninfected hepatocytes) and GUH (the highest uninfected hepatocytes) constitute the terms (fuzzy sets) of the linguistic variable UH. Similarly, LIH, NIH and GUH (respectively LFV, NFV and GFV are used for the terms of the variable linguistic IH (respectively FV).
According the relation (19), we have![]() ,
, ![]() and
and![]() . For an uninfected Hepatitis B virus, uninfected hepatocytes, infected hepatocytes and free virions change such that we can consider a universe of discourse x where the labels are centered respectively at −800, 150 and 500; 0, 150 and 300; 0, 250 and 500. Then, we suppose that theses centers constitute the operating points values of the system (20).
. For an uninfected Hepatitis B virus, uninfected hepatocytes, infected hepatocytes and free virions change such that we can consider a universe of discourse x where the labels are centered respectively at −800, 150 and 500; 0, 150 and 300; 0, 250 and 500. Then, we suppose that theses centers constitute the operating points values of the system (20).
The operating points associated to those linguistic variables are given in the Table 1, membership functions associated to this labeling are represented in the Figures 1-3.
Let us set ![]() and
and![]() , using parameters values from Table 2.
, using parameters values from Table 2.
The relations (24), (25) and (26) give respectively the following matrices
![]()
![]()
Table 1. Variables and their operating points.
![]()
Table 2. Parameters used in numerical simulation.
![]()
![]()
It is easy to note that the problem (29)-(30) is a linear quadratic (LQ). Since there are three linear state systems, the solution leads to three feedback controls of the form
![]() (51)
(51)
where ![]() is a gain feedback.
is a gain feedback.
The implementation can be made in several platforms. Here we use MATLAB package. Taking ![]() and
and ![]() of the relation (28) as identity matrices of size 3 and 2 respectively, we obtain from the relation (31)
of the relation (28) as identity matrices of size 3 and 2 respectively, we obtain from the relation (31)
![]()
The defuzzification transformation allows obtaining one system. Consequently, for the system (30) this technique gives the following system
![]() (52)
(52)
where A and B are 3 × 3 and 3 × 2 matrices and c a 3 × 1 matrix.
In the same way, from the matrixes K1, K2 and K3 the defuzzification process allows to have one matrix K. We propose the following procedure.
The rows of matrixes![]() ,
, ![]() ,
, ![]() and
and![]() ,
, ![]() are defuzzified as given by the relation () and using the degree of membership
are defuzzified as given by the relation () and using the degree of membership ![]() and
and ![]() (see the Figure 1),
(see the Figure 1), ![]() and
and ![]() (see the Figure 2) and
(see the Figure 2) and ![]() and
and ![]() (see the Figure 3). This manner of procedure is due to the two following reasons.
(see the Figure 3). This manner of procedure is due to the two following reasons.
1) We consider the degree of membership of the entry uninfected hepatocytes, infected hepatocytes and free virions respectively. These values are respectively 400 cells/dl (see the Figure 1), 120 cells/dl (see the Figure 2) and 180 cells/dl (see the Figure 3). After calculations, the Table 3 shows the obtained degrees of membership of each linguistic variable.
2) Each equation of the system (22) has nonlinear factor.
Considering these hypothesis and from the relation (18) where we take degrees of membership as given in the Table 3, we have the following matrixes.
![]()
![]()
Table 3. Variables and their corresponding degrees of membership.
The numerical simulation gives the graphical results given in the Figure 4 and Figure 5.
The Figure 4 illustrates both chemotherapy ![]() that is used to prevent the virus from infecting the cell (Figure 4(a)) and chemotherapy
that is used to prevent the virus from infecting the cell (Figure 4(a)) and chemotherapy ![]() that allows the prevention of the infected cells from producing the new viruses (Figure 4(b)). Figure presents the response of these chemotherapy to variation of the concentration of uninfected hepatocytes (Figure 5(a)), infected hepatocytes (Figure 5(b)) and free virions (Figure 5(c)) respectively.
that allows the prevention of the infected cells from producing the new viruses (Figure 4(b)). Figure presents the response of these chemotherapy to variation of the concentration of uninfected hepatocytes (Figure 5(a)), infected hepatocytes (Figure 5(b)) and free virions (Figure 5(c)) respectively.
![]()
Figure 4. Variation of drugs (control) u1 (a) and u2 (b). The curves in dotted line represent the parameter for the the direct approach. The curve dashed line show the parameter for the approach integrating the fuzzy logic approach.
![]()
Figure 5. Variation of the concentration of uninfected hepatocytes (a), infected hepatocytes (b) and free virions (c) for a patient. The curves in dotted line represent the parameter for the direct approach. The curve dashed line show the parameter for the direct approach. The curve dashed line show the parameter for the approach integrating the fuzzy logic approachThe curve dashed line show the parameter for the approach integrating the fuzzy logic.
It is known that acute hepatitis B infection (short-term inflammation of the liver) goes away on its own since the immune system is able to clear the virus from the body. The patient of acute hepatitis B infection may not need treatment. The main aim of treatment for chronic hepatitis B is to suppress HBV replication before there is irreversible liver damage. Furthermore, the role of drugs on chronic hepatitis B virus is to reduce the risk of liver disease and prevent you from passing the infection to others. The controls variation of hepatitis B virus are represented in Figure 4 which shows the decrease from 1 (when and treatment is absent) of both chemotherapy ![]() and chemotherapy
and chemotherapy ![]() to be closer to the lower value 0 (maximal use of therapy). The Figure 5(a) shows a increase of uninfected hepatocytes to its higher value during the first month of the beginning of the process before decreasing to reach the wanted equilibrium value. This behaviour is due to action of therapeutic drugs. The Figure 5(b) and Figure 5(c) illustrate that both infected hepatocytes and free virions decrease from starting time of taking therapeutic drugs to normal value. The results obtained in this work are rather satisfactory. In particular, the reaction of the disease to drugs can be modeled and a feedback can be approximated by the solution of a linear quadratic problem. The drugs reduce the risk of disease. Therefore the drugs play a crucial role such that any patient becomes healthy.
to be closer to the lower value 0 (maximal use of therapy). The Figure 5(a) shows a increase of uninfected hepatocytes to its higher value during the first month of the beginning of the process before decreasing to reach the wanted equilibrium value. This behaviour is due to action of therapeutic drugs. The Figure 5(b) and Figure 5(c) illustrate that both infected hepatocytes and free virions decrease from starting time of taking therapeutic drugs to normal value. The results obtained in this work are rather satisfactory. In particular, the reaction of the disease to drugs can be modeled and a feedback can be approximated by the solution of a linear quadratic problem. The drugs reduce the risk of disease. Therefore the drugs play a crucial role such that any patient becomes healthy.
5. Concluding Remarks
In this work, we have been dealing with an optimal control problem related to an uninfected hepatitis B virus dynamics. To handle that problem, two numerical approaches have been compared to determine the optimal trajectories of uninfected hepatocytes, infected hepatocytes and free virions as response to hepatitis B virus controls that is two drugs, interferon and ribavirin. The findings show that those two used methods are satisfactory and provide the closer results. Consequently, the approach that involves fuzzy logic approach can be seen to play an important role for the resolution of the optimal control problem. In particular, it gives the optimal trajectories and in the same way it ensures healthy.