1. Introduction
Cross validation (CV) is a model evaluation technique that utilizes data splitting. To describe CV, suppose that each data observation consists of a response value (the dependent variable) and corresponding predictor values (the independent variables) that will be used in some specified model form for the response. The data observations are split (partitioned) into two subsets. One subset (the training set) is used for model parameter estimation. Using these parameter values, the model is then applied to the other subset (the testing set). The model predictions determined for the testing set observations are compared to their corresponding actual response values, and an “out-of-sample” mean squared error is computed. For delete-d cross validation, all possible data splits with testing sets that contain d observations are evaluated. The aggregated mean squared error statistic that results from this computational effort is denoted CV(d).
To define the CV(d) statistic used in ordinary least squares (OLS) linear regression, let p < n be positive integers, and let Ik denote the k-by-k identity matrix. Let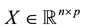 ,
, 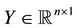 ,
, 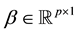 , and
, and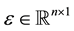 , where β and ε are unknown and
, where β and ε are unknown and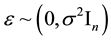 . Also, let β and ε be such that Y = Xβ + ε is the “true” optimal (minimum σ2) linear statistical model for predicting Y using X. Each row of the matrix [X Y] corresponds to a data observation (p predictors and one response), and each column of X corresponds to a particular predictor. Assume that each p-row submatrix of X has full rank, a necessary condition for CV(d) to be computable for all
. Also, let β and ε be such that Y = Xβ + ε is the “true” optimal (minimum σ2) linear statistical model for predicting Y using X. Each row of the matrix [X Y] corresponds to a data observation (p predictors and one response), and each column of X corresponds to a particular predictor. Assume that each p-row submatrix of X has full rank, a necessary condition for CV(d) to be computable for all 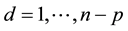 . This is a reasonable assumption when the data observations are independent. Let S be an arbitrary subset of
. This is a reasonable assumption when the data observations are independent. Let S be an arbitrary subset of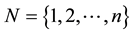 , and let SC = N\S. Let XS denote the row subset of X indexed by S, and define
, and let SC = N\S. Let XS denote the row subset of X indexed by S, and define
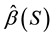 to be the OLS parameter vector estimated using XS. Define
to be the OLS parameter vector estimated using XS. Define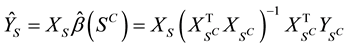 .
.
Let  denote the l2 norm and let
denote the l2 norm and let 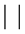 denote set cardinality. Then the delete-d cross validation statistic is given by
denote set cardinality. Then the delete-d cross validation statistic is given by
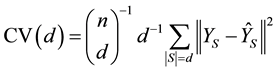 (1)
(1)
This equation can be found in [1] , [2] (p. 255), and [3] (p. 405). The form of (1) is that of a mean squared error, because there are d observations in each testing set S and there are n-choose-d unique subsets S such that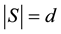 .
.
2. Background for CV(d)
Three popular papers provided some of the early groundwork for cross validation. Allen [4] introduced the prediction sum of squares (PRESS) statistic, which involves sequential prediction of single observations using models estimated from the full data absent the data point to be predicted. Stone [5] examined the use of delete-1 cross validation methods for regression coefficient “shrinker” estimation. Geisser [6] presented one of the first introductions of a multiple observation holdout sample reuse method similar to delete-d cross validation. One of the first major practical implementations of CV appeared in [7] , where “V-fold cross validation” is offered as a way to estimate model accuracy during optimization of classification and regression tree models.
Numerous authors have discussed and examined the properties of CV(1) specifically in the context of model selection (e.g., [2] [8] [9] ). These studies and others have established that in spite of the merits of using CV(1), this method does not always perform well in optimal model identification studies when compared to other direct methods such as information criteria (e.g., [2] ). The consensus is that CV(1) has a tendency in many situations to select overly complex models; i.e., it does not sufficiently penalize for over fitting [10] (p.303). Many researchers have examined CV(d) for one or more d values for actual and simulated case studies involving model selection (e.g., [1] [2] [11] ), but not to the extent of exposing any general, finite-sample statistical tendencies of CV(d) as a function of d.
Asymptotic equivalence of CV(1) to the delete-1 jackknife, the standard bootstrap, and other model selection statistics such as Mallows’s Cp [12] and the Akaike information criteria (AIC) [13] has been established (see [11] & [14] and references therein). By defining d to increase at a rate d/n → a < 1, Zhang [1] shows that CV(d) and a particular form of the mean squared prediction error ( [15] ; this is a generalization of the “final prediction error” of [16] ) are asymptotically equivalent under certain constraints. Arguably the most compelling result can be found in [11] , where it is shown that if d is selected such that d/n → 1 and n ? d → ∞ as n → ∞, these conditions are necessary and sufficient to ensure consistency of using CV(d) for optimal linear model selection under certain general conditions. The proof depends on a formula for E[CV(d)] that applies to the X-fixed case, and the author (Shao) briefly describes the additional constraints (which are unrelated to the E[CV(d)] formula) necessary for almost sure application of the result to the X-random case.
Unfortunately, none of these asymptotic theoretical developments provide practitioners with specific guidance or information helpful for making a judicious choice for d in an arbitrary small sample setting, for either forecast error variance estimation or model ranking for model selection. For this study, two questions are addressed regarding CV(d) that are relevant to the small sample setting. First, expressions are developed for E[CV(d)] for the X-random case using simulation, which are linked back to theory and generalized. Second, a model selection simulation is used to illustrate how Shao’s conditions {d/n → 1 and n ? d → ∞ as n → ∞} are manifested in the smallest sample setting.
3. Expected Value for CV(d)
3.1. Problem Background
For the case with X-fixed, Shao & Tu [17] (p. 309) indicate that
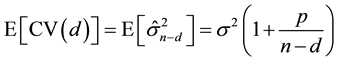 (2)
(2)
This expression implies that CV(d) provides an estimate for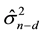 , where
, where 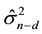 refers to the squared prediction error when making a prediction for a future observation at a design point (row of predictor matrix X) and X contains n?d independent observations (rows).
refers to the squared prediction error when making a prediction for a future observation at a design point (row of predictor matrix X) and X contains n?d independent observations (rows).
A theorem introduced in this section establishes that (2) applies to the case of the mean (intercept) model. As previously noted, we are interested in the X-random case. Based on an extremely tight correspondence with simulation results, expressions are conjectured for E[CV(d)] when the linear model contains at least one random valued predictor, for cases with and without an intercept. Building from work described in Miller [9] , the conjectured formulas are linked back to theory, allowing them to be generalized beyond the constraints of the simulation.
3.2. Results
Begin with the simplest case, where the only predictor is the intercept. Suppose X = 1n×1 (an n-vector of ones), so that the linear regression model under investigation is the mean model (so called because![]() ). The expected value for (1) under the mean model is given in
). The expected value for (1) under the mean model is given in
THEOREM 1: Suppose X = 1n×1, and let ![]() be such that the
be such that the![]() . Then, for
. Then, for![]() , the expected value for CV(d) is given by
, the expected value for CV(d) is given by
![]() (3)
(3)
Proof: Define![]() , where
, where![]() . Then, for
. Then, for![]() , we will show that the expected value for a single summand term of (1) is given by
, we will show that the expected value for a single summand term of (1) is given by
![]() .
.
The d-by-1 vector ![]() has components of the form
has components of the form![]() , where yj is a “deleted” observation (entry in YS) and
, where yj is a “deleted” observation (entry in YS) and ![]() is the sample mean of (n ? d) Y-values in
is the sample mean of (n ? d) Y-values in ![]() that were not deleted. Since yj and
that were not deleted. Since yj and ![]() are statistically independent and have the same expected value (m), we have
are statistically independent and have the same expected value (m), we have
![]() .
.
Since yj is an arbitrary element of holdout set YS, we have
![]() .
.
Because of the linearity of![]() , (3) immediately follows from this derivation, which applies to an arbitrary split of the dataset. QED
, (3) immediately follows from this derivation, which applies to an arbitrary split of the dataset. QED
Different results appear when simulating models that include at least one random valued predictor. Using the random number generator in MATLAB® to simulate data sets {X,Y}, values for CV(d) were simulated for numerous cases with ![]() and
and![]() . Y-values were simulated using Yj = Xjβ + εj, with error
. Y-values were simulated using Yj = Xjβ + εj, with error![]() ,
, ![]() ,
, ![]() , and
, and![]() . For each simulated data set, for
. For each simulated data set, for![]() , coefficient values
, coefficient values ![]() were IID Bernoulli with
were IID Bernoulli with![]() . For each simulated data set, for
. For each simulated data set, for![]() , deviation values σ = 10α and
, deviation values σ = 10α and ![]() were IID such that α,
were IID such that α, ![]() (to help limit rounding errors, α and αk values outside the interval [?3,3] were snapped to the appropriate interval endpoint). Simulations using an intercept were also examined, in which case the first column of X was populated with ones rather than random values.
(to help limit rounding errors, α and αk values outside the interval [?3,3] were snapped to the appropriate interval endpoint). Simulations using an intercept were also examined, in which case the first column of X was populated with ones rather than random values.
For a particular (n,p), after simulating at least 20,000 CV(d) values for each possible![]() , mean simulated CV(d) values were computed to provide simulated E[CV(d)]. Upon inspection, simulated E[CV(d)]/σ2 were found to follow rational number sequences clear enough to conjecture general formulas for E[CV(d)] dependent on n ? d, p, and σ2.
, mean simulated CV(d) values were computed to provide simulated E[CV(d)]. Upon inspection, simulated E[CV(d)]/σ2 were found to follow rational number sequences clear enough to conjecture general formulas for E[CV(d)] dependent on n ? d, p, and σ2.
An apparently related outcome is the identification of a two-point region of numerical instability of the E[CV(d)] error curve for any tested model that includes a random valued predictor. Specifically, simulation results reveal two points of increasing instability at ![]() and E[CV(dmax)], where dmax = n ? p. The term “increasing instability” is apt because the coefficient of variation (=standard deviation/mean) calculated for the simulated CV(d) values is stable for d < dmax ? 1, but increasingly blows up (along with E[CV(d)]) at d = dmax ? 1 and d = dmax (results not shown). The reason for this phenomenon is, at present, an interesting open question. This exceptional behavior is not incompatible with the conjectured formulas for E[CV(d)] because the formulas break down at the two largest allowable d values.
and E[CV(dmax)], where dmax = n ? p. The term “increasing instability” is apt because the coefficient of variation (=standard deviation/mean) calculated for the simulated CV(d) values is stable for d < dmax ? 1, but increasingly blows up (along with E[CV(d)]) at d = dmax ? 1 and d = dmax (results not shown). The reason for this phenomenon is, at present, an interesting open question. This exceptional behavior is not incompatible with the conjectured formulas for E[CV(d)] because the formulas break down at the two largest allowable d values.
To gauge the accuracy of the conjectured formulas for E[CV(d)], the author used an absolute percent error statistic defined by
![]() (4)
(4)
To provide a simple gauge for rounding error magnitude, values were simulated for the expected error of regression, given by
![]() (5)
(5)
REG has the property that E[REG] = σ2.
Two findings are notable: (a) distinct but related patterns for E[CV(d)] emerge when considering linear models consisting entirely of random valued predictors and those that use an intercept; and (b) two points of increasing instability appear at ![]() and E[CV(dmax)]. The existence of the two-point instability appears to be robust to increasing dimensionality. Result (a) is expressed in Conjectures 1 and 2, which do not conflict with the exceptional behavior noted in (b). For Conjectures 1 and 2, suppose that
and E[CV(dmax)]. The existence of the two-point instability appears to be robust to increasing dimensionality. Result (a) is expressed in Conjectures 1 and 2, which do not conflict with the exceptional behavior noted in (b). For Conjectures 1 and 2, suppose that![]() , with β the assumed “true” linear model coefficient vector.
, with β the assumed “true” linear model coefficient vector.
CONJECTURE 1: Let X be the n-by-p design matrix where p < n ? 2 and the predictors in X are multivariate normal. Then, for![]() , the expected value for CV(d) is given by
, the expected value for CV(d) is given by
![]() . (6)
. (6)
In the search for this equation, the author scrutinized simulated values for E[CV(d)], examining a variety of cases. Using the approximation in (2) as a starting point for exploring possible forms for the RHS of (6), the author eventually arrived at (6) through trial and error.
At ![]() (the first point of the two-point instability in the E[CV(d)] error curve), (6) has a singularity. At d = dmax, (6) takes the nonsensical value of
(the first point of the two-point instability in the E[CV(d)] error curve), (6) has a singularity. At d = dmax, (6) takes the nonsensical value of![]() . Though (6) and (2) are similar, the inclusion of “?p ? 1” in the denominator of the dilation factor in (6) presents an obvious disagreement that becomes increasingly substantial as p increases. For example, the largest value that (2) can achieve is 2σ2, realized at d = dmax. Compare this to the maximum E[CV(d)] value
. Though (6) and (2) are similar, the inclusion of “?p ? 1” in the denominator of the dilation factor in (6) presents an obvious disagreement that becomes increasingly substantial as p increases. For example, the largest value that (2) can achieve is 2σ2, realized at d = dmax. Compare this to the maximum E[CV(d)] value![]() , realized by (6) at
, realized by (6) at![]() .
.
Figure 1 shows results for the case![]() , with a single random valued predictor comprising the design matrix X. The simulated E[CV(d)] error curve is displayed along with corresponding predicted E[CV(d)] error curves obtained using (6) and (2), so that all three error curves can be examined simultaneously. Note the congruity between simulated E[CV(d)] and predicted E[CV(d)] from Conjecture 1, and the widening (with d)
, with a single random valued predictor comprising the design matrix X. The simulated E[CV(d)] error curve is displayed along with corresponding predicted E[CV(d)] error curves obtained using (6) and (2), so that all three error curves can be examined simultaneously. Note the congruity between simulated E[CV(d)] and predicted E[CV(d)] from Conjecture 1, and the widening (with d)
![]()
Figure 1. A comparison between simulated and predicted E[CV(d)] error curves using a linear model with a single random valued predictor, for sample size n = 10. Note the good correspondence between the simulated E[CV(d)] values and the predicted values from Conjecture 1. Also visible is the two-point instability, with simulated E[CV(d)] blowing up at d = dmax ? 1 = 8 and d = dmax = 9.
disparity between simulated E[CV(d)] and predicted E[CV(d)] from the approximation provided in (2). Also note the blowup in simulated E[CV(d)] at the two largest d values, reflecting the previously described two-point instability of the E[CV(d)] error curve when at least one random valued predictor is used in the model.
Figure 2(a) shows results for the case![]() , using a model with two random valued predictors. Figure 3(a) shows results for the case with
, using a model with two random valued predictors. Figure 3(a) shows results for the case with![]() , using a model with eight random valued predictors. The same observations noted above for Figure 1 apply to Figure 2(a) and Figure 3(a). Now consider the case where an intercept is included in the linear model.
, using a model with eight random valued predictors. The same observations noted above for Figure 1 apply to Figure 2(a) and Figure 3(a). Now consider the case where an intercept is included in the linear model.
CONJECTURE 2: Let X be the n-by-p design matrix where p < n ? 2, the first column of X is an intercept, and the other predictors in X are multivariate normal. Then, for![]() , the expected value for CV(d) is given by
, the expected value for CV(d) is given by
![]() . (7)
. (7)
In the search for this equation, the author once again scrutinized simulated values for E[CV(d)], examining a variety of cases. This time, (6) was used as a starting point for exploring possible forms for the RHS of (7). Specifically, the author reasoned that substitution of an intercept for a random valued predictor reduces model complexity, suggesting that the E[CV(d)] expression for models that include an intercept might take the form of a dampened version of (6). Indeed, after much trial and error, this was found to be the case once the RHS of (7) was “discovered”.
Like Equation (6), at ![]() and
and![]() , (7) has a singularity and a non-positive (and thus nonsensical) value, respectively. Note that (7) constitutes a downward adjustment of (6). Apparently, the 1/(n?d) term provides an adjustment for the reduced model complexity when substituting an intercept for a random-valued predictor. The 2/p term dampens the adjustment as p gets larger and the general effect of this substitution on the model becomes less pronounced.
, (7) has a singularity and a non-positive (and thus nonsensical) value, respectively. Note that (7) constitutes a downward adjustment of (6). Apparently, the 1/(n?d) term provides an adjustment for the reduced model complexity when substituting an intercept for a random-valued predictor. The 2/p term dampens the adjustment as p gets larger and the general effect of this substitution on the model becomes less pronounced.
Figure 2(b) shows results for the case![]() , using a model with an intercept and one random valued predictor. Figure 3(b) shows results for the case
, using a model with an intercept and one random valued predictor. Figure 3(b) shows results for the case![]() , using a model with an intercept and seven random valued predictors. The same general observations noted above for Figure 1 apply to Figure 2(b) and Figure 3(b).
, using a model with an intercept and seven random valued predictors. The same general observations noted above for Figure 1 apply to Figure 2(b) and Figure 3(b).
![]()
Figure 2. A comparison between simulated and predicted E[CV(d)] error curves using a linear model with (a) two random valued predictors, and (b) an intercept and one random valued predictor, for sample size n = 10. Note the good correspondence between the simulated E[CV(d)] values and the predicted values from Conjectures 1 and 2. Also visible is the two-point instability, with simulated E[CV(d)] blowing up at d = dmax ? 1 = 7 and d = dmax = 8.
![]()
Figure 3. A comparison between simulated and predicted E[CV(d)] error curves using the linear model with (a) eight random valued predictors, and (b) an intercept and seven random valued predictors, for sample size n = 20. Note the good correspondence between the simulated E[CV(d)] values and the predicted values from Conjectures 1 and 2. Also visible is the two-point instability, with simulated E[CV(d)] blowing up at d = dmax ? 1 = 11 and d = dmax = 12.
These simulation results using independent normal predictors and errors provide strong evidence for the validity of Conjectures 1 and 2. Graphical evidence for this assertion can be seen in Figures 1-3. APE values (4) computed comparing (6) and (7) to corresponding simulated E[CV(d)] were generally O(10−2) to O(10−1). To provide a gauge for these error magnitudes, E[REG] values (5) were simulated and compared to the known value of σ2. APE values from this comparison also were generally O(10−2) to O(10−1), indicating that rounding error was solely responsible for the slight differences observed between simulated E[CV(d)] and predicted E[CV(d)] from (6) and (7). To justify the more general assumptions in the conjectures using multivariate normal predictors and second-order errors, we use the following theoretical connection.
3.3. Connecting Simulation Results Back to Theory
Equation (2) was examined because it was the only explicitly stated estimate for E[CV(d)] found in the literature. This expression gives the expected mean squared error of prediction (MSEP) for using a linear regression model to make a prediction for some future observation at a design point. However, (2) provides an inaccurate characterization for CV(d) in any arbitrary small sample setting where there are substantially more possible design point values than observations. In this situation, the random subset design used for making “out-of-sample” predictions when computing the CV(d) statistic more logically is associated with the expected MSEP for using a linear regression model to make a prediction for some future observation at a random X value.
In Miller [9] (pp. 132-133), an expression is derived for E[MSEP] in the random X case, using a model with an intercept and predictor variables independently sampled from some fixed multivariate normal distribution and general second order errors with mean 0 and variance σ2. Miller credits this result to [18] , but uses a derivation from [19] . The equation that Miller derives is
![]() . (8)
. (8)
The “1/n” term in the dilation factor accounts for the variance of the intercept parameter estimated in the model. The other term in the dilation factor is developed using a Hotelling T2-statistic, which is a generalization of Student’s t-statistic that is used in multivariate hypothesis testing. If we replace n ? d with n in (7), then it is easy to show that (8) and (7) are equivalent.
Following Miller’s derivation for the case using a model with an intercept, we can also derive an expression equivalent to (6) for the “no intercept” case. The “1/n” term in (8) is not needed because all predictor and response variables are distributed with 0 mean, and no intercept is used in the model. It is a straightforward exercise to show that the other term in the dilation factor becomes![]() , giving
, giving
![]() . (9)
. (9)
(9) is identical to (6) if we substitute n for n ? d in (6).
In support of the error generalization, simulations using ![]() (where a is randomly drawn from the interval
(where a is randomly drawn from the interval ![]() for each simulated data set) were found to produce APE values on the same order as those observed using normally distributed ε. Regarding the normality constraint on X, if we independently sample pre-
for each simulated data set) were found to produce APE values on the same order as those observed using normally distributed ε. Regarding the normality constraint on X, if we independently sample pre-
dictor values from![]() , then simulated E[CV(d)] values are less than the conjectured values.
, then simulated E[CV(d)] values are less than the conjectured values.
For example, with ![]() and no intercept, E[CV(d)] values ranged from 2.8% - 9.6% smaller than the conjectured formula in (6) as d increased from 1 to (dmax ? 2), but simulated E[REG] values were unchanged (as expected, since E[REG] is independent of predictor distribution). Therefore, unlike some of the more general properties for OLS linear regression, E[CV(d)] appears to depend on predictor distribution. It is worth noting that the two-point instability phenomenon persisted in the uniformly distributed X case and thus appears to be robust to predictor distribution.
and no intercept, E[CV(d)] values ranged from 2.8% - 9.6% smaller than the conjectured formula in (6) as d increased from 1 to (dmax ? 2), but simulated E[REG] values were unchanged (as expected, since E[REG] is independent of predictor distribution). Therefore, unlike some of the more general properties for OLS linear regression, E[CV(d)] appears to depend on predictor distribution. It is worth noting that the two-point instability phenomenon persisted in the uniformly distributed X case and thus appears to be robust to predictor distribution.
3.4. Simulating CV(d) for Model Selection in a Small Sample Setting
Recall the asymptotic model selection conditions from [11] requiring that d/n → 1and n ? d → ∞ as n → ∞. The conclusion to be drawn from these constraints is that when using CV(d) for model ranking in model selection, a value for d that is an appreciable fraction of sample size n is preferred. However, no specific guidance is provided, as the finite sample situation is inconsequential to the asymptotic result. For example, setting![]() ,
, ![]() , satisfies Shao’s two conditions, yet imposes no certain constraint on what values for d are desirable.
, satisfies Shao’s two conditions, yet imposes no certain constraint on what values for d are desirable.
To use CV(d) for model selection in a manner that is consistent with Shao’s setup, one begins with a pool of candidate predictors and evaluates all possible linear models defined by non-empty subsets of this predictor pool for the purpose of estimating some response. The optimal model contains only and all of the predictors that contribute to the response. CV(d) is evaluated for each candidate model, and the model exhibiting the smallest CV(d) value is selected. Define the optimal d value (dopt) to correspond with the CV(d) that exhibits the highest rate of selecting the optimal model. If Shao’s result has relevance in the small sample setting, one would expect dopt to generally be among the larger allowable d values. Further, we would expect dopt to increase nearly at the same rate as n, while at the same time also observing growth in n ? dopt.
For this simulation, define predictor pool![]() , which consists of an intercept and two random variables that are
, which consists of an intercept and two random variables that are![]() , where n is sample size. From this three-element predictor pool, there are seven candidate models defined by the non-empty subsets. Values for response variable Y were simulated using
, where n is sample size. From this three-element predictor pool, there are seven candidate models defined by the non-empty subsets. Values for response variable Y were simulated using ![]() , where error
, where error![]() . The optimal model is defined by the choice for
. The optimal model is defined by the choice for
![]() used to construct Y, for which five values were examined representing the unique cases:
used to construct Y, for which five values were examined representing the unique cases:
![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and![]() . For each sample size n = 4:20, at least 12,000 iterations (i.e., model selection opportunities) were simulated for each choice for β. For each iteration, CV(d) values were computed for
. For each sample size n = 4:20, at least 12,000 iterations (i.e., model selection opportunities) were simulated for each choice for β. For each iteration, CV(d) values were computed for ![]() for each of the seven candidate models, with the upper bound for d (called dub) determined by the largest allowable d for the full model (which uses all three predictors). For each d, the model with the smallest CV(d) value was identified, allowing for a rate of optimal model selection to be estimated across the iterations. For comparison, REG values also were computed and evaluated for optimal model selection rate.
for each of the seven candidate models, with the upper bound for d (called dub) determined by the largest allowable d for the full model (which uses all three predictors). For each d, the model with the smallest CV(d) value was identified, allowing for a rate of optimal model selection to be estimated across the iterations. For comparison, REG values also were computed and evaluated for optimal model selection rate.
Optimal model selection rates using model selectors CV(d) and REG (which is plotted at d = 0 for convenience) are shown in Figures 4(a)-(e) for the five unique optimal model cases, followed by the average optimal model selection rate in Figure 4(f) reflecting the case where the optimal model can be any one of the seven candidate models. To compute the average, results from optimal model cases ![]() and
and ![]() were doubly weighted to account for the redundant cases
were doubly weighted to account for the redundant cases ![]() and
and ![]() that were not separately simulated.
that were not separately simulated.
At the extreme cases ![]() (Figure 4(a); the intercept model) and
(Figure 4(a); the intercept model) and ![]() (Figure 4(e); the full model), we see dopt = dub and dopt = 1, respectively, for all examined n. For cases in between (Figures 4(b)-(d)), dopt varies with n in a generally logical progression. Ultimately we are interested in the behavior of dopt in the arbitrary case, where the optimal model can be any one of the seven candidate models. This situation is depicted in Figure 4(f), which shows the average behavior of CV(d) and REG for model selection. Indeed, dopt does appear to exhibit behavior not unlike that implied by Shao’s conditions, suggesting that the essence of Shao’s asymptotic result may well have applicability in this most elementary of model selection scenarios, and perhaps the small sample model selection setting in general.
(Figure 4(e); the full model), we see dopt = dub and dopt = 1, respectively, for all examined n. For cases in between (Figures 4(b)-(d)), dopt varies with n in a generally logical progression. Ultimately we are interested in the behavior of dopt in the arbitrary case, where the optimal model can be any one of the seven candidate models. This situation is depicted in Figure 4(f), which shows the average behavior of CV(d) and REG for model selection. Indeed, dopt does appear to exhibit behavior not unlike that implied by Shao’s conditions, suggesting that the essence of Shao’s asymptotic result may well have applicability in this most elementary of model selection scenarios, and perhaps the small sample model selection setting in general.
Additional simulation results (Figure 5) using 80% shared variance (correlation) between X1 and X2 exhibit similar behavior but with lower and flatter CV(d) rate curves (i.e., reduced capability for optimal model selection and less distinction for dopt) and attenuated growth in dopt. Though this situation does not precisely conform to Shao’s setup, it is valuable none the less because model selection situations using real data frequently involve correlated predictors.
4. Conclusions
The first objective of this research was to examine values of E[CV(d)] in a small sample setting using simulation. This effort resulted in Conjectures 1 and 2, which constitute the first explicitly stated, generally applicable formulas for E[CV(d)]. The link established between (6) and (7) and the random-X MSEP described in [9] allowed for the generalization of Conjectures 1 and 2 beyond the limited scope of the simulation, to multivariate normal X and![]() . Simulation using uniformly distributed predictors suggested that the E[CV(d)] statistic does depend on predictor distribution.
. Simulation using uniformly distributed predictors suggested that the E[CV(d)] statistic does depend on predictor distribution.
Revelation of the two-point numerical instability at the end of the E[CV(d)] error curve, which was not incompatible with the conjectured formulas for E[CV(d)] because of their breakdown at these values, was an
![]()
Figure 4. Optimal model selection rates are shown for the model selection simulation using a candidate predictor pool {1, X1, X2}, for sample sizes n = 4:20. Optimal d values (dopt) are circled. Results for particular optimal models (predictor subsets) are shown in (a) {1}; (b) {X1} (or {X2}); (c) {1,X1} (or {1,X2}); (d) {X1,X2}; and (e) {1,X1,X2}. β values correspond to notation used in the text. (f) shows the average model selection rate across (a)-(e), with (b) and (c) double counted in the average for completeness.
unexpected outcome. This phenomenon, which did not appear to depend on predictor distribution, suggests the curious result that OLS linear regression models fit using just 1 or 0 degrees of freedom must be unique in some way compared to models fit using 2 or more degrees of freedom. Theoretical investigation of this exceptional behavior might best begin by examining the development of the Hotelling T2-statistic for the multivariate normal X case that provides the basis for the X-random MSEP in (8).
For the second objective, an elementary model selection simulation with candidate predictors![]() , where X1 and X2 were
, where X1 and X2 were![]() , was used to show how the asymptotic model selection conditions {d/n → 1and n ? d → ∞ as n → ∞} of [11] are manifested in the smallest sample setting. When the optimal model was the full model (i.e., the most complex model), then CV(1) was the best model ranking statistic (dopt = 1). When the optimal model was the mean model (i.e., the simplest model), then CV(dub) was the best model ranking statistic (dopt = dub). For cases in between, dopt was observed to vary with n in a generally logical progression dependent on optimal model complexity. Ultimately we are interested in the arbitrary optimal model case, which was simulated by averaging all of the specific optimal model selection rates. For the arbitrary optimal model case, dopt and optimal model selection rate demonstrated behavior reflective of the conditions prescribed in [11] , whereby (i) the optimal model selection rate at d = dopt increased as n increased, (ii) dopt was generally among the larger allowable d values, (iii) dopt increased at nearly the same rate as n, and (iv) growth occurred in n ? dopt. These behaviors persisted in a dampened fashion when correlated predictors were used, with faster growth observed in n ? dopt.
, was used to show how the asymptotic model selection conditions {d/n → 1and n ? d → ∞ as n → ∞} of [11] are manifested in the smallest sample setting. When the optimal model was the full model (i.e., the most complex model), then CV(1) was the best model ranking statistic (dopt = 1). When the optimal model was the mean model (i.e., the simplest model), then CV(dub) was the best model ranking statistic (dopt = dub). For cases in between, dopt was observed to vary with n in a generally logical progression dependent on optimal model complexity. Ultimately we are interested in the arbitrary optimal model case, which was simulated by averaging all of the specific optimal model selection rates. For the arbitrary optimal model case, dopt and optimal model selection rate demonstrated behavior reflective of the conditions prescribed in [11] , whereby (i) the optimal model selection rate at d = dopt increased as n increased, (ii) dopt was generally among the larger allowable d values, (iii) dopt increased at nearly the same rate as n, and (iv) growth occurred in n ? dopt. These behaviors persisted in a dampened fashion when correlated predictors were used, with faster growth observed in n ? dopt.
![]()
Figure 5. Same as Figure 4(f), but with X1 and X2 values simulated such that Corr(X1,X2) ≈ 0.8. Optimal d values (dopt) are indicated by dots. Results from Figure 4(f) are shown in the background for comparison.
For practitioners, the analyses presented in this paper shed new light on computed CV(d) values, especially for small sample model selection and forecast error variance estimation problems where little is known about the behavior of CV(d). With the conjectured formulas for E[CV(d)] (which appear to be exact for the multivariate normal case), theoreticians can formulate more precise series expansions for CV(d) to facilitate the furthering of our mathematical understanding of this interesting and useful statistic.