1. Introduction
Robotic applications, especially robotic arm, become widely used in industries due to their simplicity and the ability to do multi-task/multi-function with few numbers of settings and/or arrangements. The problem with such applications is the necessary to apply nonlinear control signals to achieve the desired trajectories. The latter is not easy to be implemented and has several limitations [1] -[3] . For example, Sliding Mode Control (SMC) [1] is one of the robust control approaches. However, it suffers from chattering. Although several researches have proposed to eliminate the chattering, the problem is still not fully solved. The limitation of such controllers increases as uncertainties present, i.e. modeling uncertainties and noise. This becomes worse when the number of measurement is less than the number of states.
Filters, especially model based filters [2] - [7] , have been used to remove some of those constrains. It is a cheap method that could be used to obtain the unmeasured-hidden-states, and/or it could be used to reduce the noise effect. The optimal solution for such applications in their linear case is the Kalman Filter (KF) [7] - [12] . When the system is nonlinear, the KF is modified to be applicable for such applications. Several researches have been developed to overcome this limitation. Those include linearizing the system by Taylor Series Approximation (TSA) up to the first order such as the Perturbation Kalman Filter [9] [13] [14] , the Extended Kalman filter (EKF) [8] [15] - [17] , and the Iterated Extended Kalman filter (IEKF) [7] [15] [18] - [20] , or up to higher order such as the Higher Order Extended Kalman Filter (HOEKF) [15] [21] - [23] . The later shows that in order to increase the accuracy of high nonlinear application, TSA is not a suitable approach as it takes long computation time with complicated structure [24] . Therefore, different approaches were developed including the combination of KF with intelligent techniques such as [25] - [29] , or finding different approaches to approximate the nonlinearity such as the Sigma-Point Kalman Filter (SPKF) [2] [4] [5] and the Particle Filter (PF) [30] . The rest of the paper will be divided as the following: Section two includes an introduction to the SPKF including the algorithms used in this paper, UKF, CKF and CDKF. The mathematical model of the PRRR robotic arm application is showed in Section three. Results, discussion and conclusion are listed and discussed in Sections four and five.
2. The Sigma-Point Kalman Filter
The SPKFs linearize the nonlinear models statistically using weighted linear regression method. This is done by obtaining a certain number of points, referred to as sigma points, from the state neighborhood using the probability distribution function as shown in Figure 1. Those points are projected through the system model, and then combined together using appropriate weights as shown in Figure 2. This provides with a mechanism that covers
![]()
Figure 2. (a) The actual system states and their nonlinear measurement; (b) The Sigma-Points KF’s estimates [31] .
the actual mean and covariance without the need to linearize the model by TSA and calculate the Jacobian matrices. Moreover, it accommodates noise disturbances that are not Gaussian [4] [5] [15] [31] - [34] .
Several algorithms have been created using the above principle. Although, different approaches were used to derive those algorithms, the general outline remain the same as will be proven in the next subsections. The major differences between those methods could be summarized to the number of the sigma points, how to choose them, and what are the appropriate weights for the combining step. Moreover, they may differ on calculating the covariance matrices [35] . Some SPKFs algorithm will be described on the next subsections.
2.1. The Unscented Kalman Filter
The Unscented Kalman Filter is a SPKF that has been developed using the unscented transformations. The latter has several form including general unscented [15] , simplex unscented [35] [36] , and spherical unscented [36] [37] , transformations. The structures of the resulting filters are similar and could be summarized by the pseudo code of Table 1, where 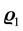 and
and  are parameters used to select the sigma points for the a priori and a posteriori estimates, respectively. Those differ from a filter to another and it result on obtaining different sigma points. Consequently, different number of sigma points and different associated weights are obtained. Those are illustrated by Table 2.
are parameters used to select the sigma points for the a priori and a posteriori estimates, respectively. Those differ from a filter to another and it result on obtaining different sigma points. Consequently, different number of sigma points and different associated weights are obtained. Those are illustrated by Table 2.
![]()
Table 1. Thepseudocode of the unscented kalman filter [2] [3] [15] [24] .
![]()
Table 2. The differences between the UKF methods [15] .
The statistical regression used in unscented filters provides with better approximation that the Jacobian matrices. It has been proven that UKFs approximates up to a third order TSA for Gaussian distributions [15] , and second order TSA for non-Gaussian distributions [31] . Both, the simplex and the spherical unscented KFs are used to reduce the computational time; as they use less sigma points. However, their stability is limited for few order of TSA [15] [37] . The general UKF provide with better estimation compared to the previous two. However, it has a larger computational time.
2.2. The Cubature Kalman Filter
The Cubature Kalman filter (CKF) is derived by using the third-degree cubature rule to numerically approximate the Gaussian-weighted integrals defined as [38] [39] :
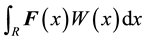 (2.1)
(2.1)
where 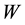 is the weight function and it is Gaussian with the form
is the weight function and it is Gaussian with the form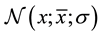 ,
, 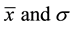 are the Gaussian’s
are the Gaussian’s
mean and standard deviation. Assuming that the states are Gaussian as well, a scheme similar to the UKF could be obtained. However, due to the Gaussian Nature, the covariance matrices will differ from those obtained from UKF. Those are illustrated by Table 3.
2.3. The Central Difference Kalman Filter
The Central Difference Kalman Filter (CDKF), described in [40] - [42] , was derived in two major stages. The first stage was to linearize the system model using TSA. In the second stage, the derivatives were replaced with their numerical Stirling’s polynomial interpolation forms (NSPI) [43] , that is defined as the follow [44] :
![]()
Table 3. Thepseudocode of the cubature kalman filter [38] [39] .
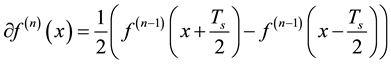 (2.2)
(2.2)
The previous stages result on a scheme that is similar to the weighted regression of the UKF as shown in Table 4. However, it differs from the UKF on how to obtain the sigma points, how to calculate the weights, and how to calculate the covariance matrices. The CDKF has been found to have a superior performance among the
other SPKFs [15] [30] [45] . Moreover, the CDKF uses one control parameter,  , which derived in [45] to have a value of
, which derived in [45] to have a value of 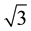 for Gaussian distributions.
for Gaussian distributions.
3. PRRR-Mathematical Model
The algorithms in section two are applied to a four DOF robotic arm that consists of one prismatic joint and three revolute joints (PRRR) that is presented by Figure 3 and Figure 4. The model has been derived in [1] and [2] , and is summarized as follow.
 (3.1)
(3.1)
![]()
Figure 3. Four-DOFPRRR Robotic Arm [1] [2] .
![]()
Figure 4. Top view of the PRRR Robotic Arm [1] [2] .
![]()
Table 4. The pseudocode of sigma-point central difference kalman filter [45] .
![]() (3.2)
(3.2)
where;
![]() (3.3)
(3.3)
![]() (3.4)
(3.4)
![]() (3.5)
(3.5)
![]() (3.6)
(3.6)
![]() (3.7)
(3.7)
![]() (3.8)
(3.8)
![]() (3.9)
(3.9)
The system is discretized using the following definition
![]() (3.10)
(3.10)
where ![]() is the sampling time and it is equal to 0.001 sec. If the states defined as the following.
is the sampling time and it is equal to 0.001 sec. If the states defined as the following.
![]() (3.11)
(3.11)
And knowing that
![]() (3.12)
(3.12)
![]() (3. 13)
(3. 13)
![]() (3.14)
(3.14)
Then the overall state space could be defined as
![]() (3. 15)
(3. 15)
Equations (3.3)-(3.9) have several parameters. Those are summarized by Table 5.
4. Results
The system in section 3 was simulated several time -for each filter including UKF, CKF and CDKF-. Four cases were obtained as follows:
1. Assuming all the states were measured.
2. Assuming that the position and angles were measured while their derivatives were not measured.
3. Similar to the first case. However, modeling uncertainties were injected; e.g. the masses were multiplied by 1.5.
4. Similar to the second case. However, modeling uncertainties were injected; e.g. the masses were multiplied by 1.5.
4.1. Results for System without Uncertainties; Cases 1 and 2
The results of cases 1 and 2 were summarized by Table 6 and Table 7. The results showed that the filters gave similar performance for all the states when no modeling presented, refer to Figure 5 and Figure 6. The performance of the filters for measured states were better than those obtained for non-measured states.
4.2. Results with Uncertainties
When modeling errors presented, the RMSE increased as shown in Table 8 and Table 9. However, their effect became large, and maybe unstable, for the states that were not measured as shown in Figure 7. In such cases, the CDKF showed the superior performance; the filter remained stable. However, the UKF and CKF had a poor performance. The errors were bounded. However, they were high, refer to Figures 8-10.
![]()
Figure 5. The performance of the filters for the third angler velocity, cases 1 and 2.
![]()
Table 5. Parameters’ Value for the robotic arm.
![]()
Figure 6. The performance of the filters for the fourth angler velocity, cases 1 and 2.
![]()
Figure 7. The performance of the filters for the fourth angler velocity, case 4.
![]()
Table 6. The root mean square error for the filters UKF, CKF and CDKF for case 1.
![]()
Figure 8. The error in estimating the fourth angular velocity using UKF for all cases.
![]()
Figure 9. The error in estimating the fourth angular velocity using CKF for all cases.
![]()
Table 7. The root mean square error for the filters UKF, CKF and CDKF for case 2.
![]()
Figure 10. The error in estimating the fourth angular velocity using CDKF for all cases.
![]()
Table 8. The root mean square error for the filters UKF, CKF and CDKF for case 3.
![]()
Table 9. The root mean square error for the filters UKF, CKF and CDKF for case 4.
5. Conclusion
This work discussed the benefits of using Sigma-Point Kalman Filters in nonlinear application, i.e. PRRR robotic arm. Three types of SPKFs were used, namely Unscented, Cubature, and Central difference Kalman Filters. Four cases were used: the first and the second cases involved with system with no modeling errors; the third and the fourth cases involved with system injected with uncertainties. The first and the third cases assumed all the states were measured which was not the case in the other cases. The results showed that the filters gave good performance when all the states were measured. Reducing the number of measurements affected the results a little bit. The errors became larger than 10 times of those obtained in case 1 when modeling errors were presented and not all the states were measured. However, the CDKF showed stable performance in all cases. The latter gave an indication to use the CDKF in such applications.
Nomenclature