Universality in Statistical Measures of Trajectories in Classical Billiard Systems ()
1. Introduction
The idea to model apparently disordered spectra, like those of heavy nuclei, using random matrices was sug- gested in the mid-50’s by Wigner, and then formalized in the early 60’s in the work of Dyson and Mehta [1] -[6] . They showed that random matrices of Gaussian orthogonal ensembles (GOE) generate a Wigner-type nearest- neighbour level spacing (NNS) distribution [6] . In a seminal paper, Bohigas, Giannoni and Schmit (BGS) for- mulated a conjecture [7] stating that time-reversal invariant quantum systems with classically fully chaotic (ergodic) counterpart have universality properties given by random matrix theory (RMT). Experiments in nu- clear physics, for example, have shown that spectra originating from different heavy nuclei give the same Wignerian energy level spacing distribution [8] . Universality properties in quantum chaos of bound systems, i.e. quantum systems with a fully chaotic classical counterpart, have now been demonstrated in many experiments, computational models and in theoretical studies [6] [9] -[14] . Theoretical support of the BGS conjecture came from the semiclassical theory of spectral rigidity by Berry [15] [16] , who showed that universal behaviour in the energy level statistics is due to long classical orbits. Sieber and Richter [17] investigated the role of correlations between classical orbits. The semiclassical theory has been further developed by Müller et al. [18] [19] . In ref. [19] they presented the “core of a proof” of the BGS conjecture, which, by proving arguments previously used by Berry [15] , show that in the semi-classical limit the periodic classical orbits determine the universal fluctua- tions of quantum energy levels. Further refinements have been made by Keating and Müller [20] .
The study of classical strongly chaotic systems (Anosov systems) has revealed that central limit theorems (CLT) hold [21] -[26] . This has been proven for the 2D periodic Lorentz gas with finite horizon. The first step of a proof was given by Bunimovich and Sinai [21] and was completed by Bunimovich, Sinai and Chernov [23] . At macroscopic times, such deterministic chaotic system converges to Brownian motion, i.e. behaves like a random system [21] [23] [24] [26] . This is also supported by the existence of an average diffusion coefficient [21] [23] [27] , showing the diffusive character of such chaotic system.
Do classical fully chaotic systems also exhibit universality properties? This question was addressed by Argaman et al. [28] , who showed that there is universal behaviour in 2 points correlation functions of actions of periodic orbits of classically chaotic systems. As examples they considered the deformed cat-map and the baker-map. This has been elaborated further in a number of studies by Dittes et al. [29] , Aurich and Sieber [30] , Cohen et al. [31] , Tanner [32] , Sano [33] , Primack and Smilansky [34] , Sieber and Richter [17] and Smi- lansky and Verdene [35] . Argaman et al. started from the assumption that spectral fluctuations of chaotic quantum systems follow the predictions of RMT and they derived a universal expression for classical cor- relation functions of periodic orbits via Gutzwiller’s semi-classical trace formula. They concluded “The real challenge, though, is to find out whether these action correlations can be explained on a completely classical level”.
An answer was proposed by Laprise et al. [36] [37] who found universal behaviour in classical 2D billiards by looking at fluctuations in spectra of classical action/length matrices from billiard trajectories. They showed that one could distinguish chaos from integrability in classical systems using RMT and an analogue of the BGS- conjecture. In particular, they considered the Limaçon/Robnik family of billiards, which interpolates between the chaotic cardiod billiard and the integrable circular billiard. For the cardioid billiard, the level spacing dis- tribution 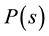 and spectral rigidity
and spectral rigidity  were found to be consistent with the GOE behaviour predicted by RMT. For the interpolating case close to the circle, the behaviour approached a Poissonian distribution. The circular billiard itself was found to be very rigid and strongly correlated and yielded
were found to be consistent with the GOE behaviour predicted by RMT. For the interpolating case close to the circle, the behaviour approached a Poissonian distribution. The circular billiard itself was found to be very rigid and strongly correlated and yielded . The jump in behaviour at the transition to the circle is associated with the corresponding change in the symmetry group.
. The jump in behaviour at the transition to the circle is associated with the corresponding change in the symmetry group.
This article extends the results of reference [36] in the following directions: 1) We consider the 2D rec- tangular billiard as another example of an integrable billiard. Compared to the circular billiard, this billiard has lower symmetry (no group property). Nevertheless, it displays strong spectral correlation and rigidity like the circular billiard. 2) We present numerical studies for other chaotic 2D billiards: the Sinai-billiard and the Bunimovich stadium billiard. 3) In order to understand the observed universal behaviour in chaotic billiards, we present arguments linking such behaviour to CLTs, diffusive and random walk behaviour. In particular, we present a mathematically rigorous result on the distribution of length of trajectories.
The answers we found can be summarized as follows: For the 2D Sinai billiard and the 2D Bunimovich stadium billiard the level spacing distribution 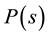 and spectral rigidity
and spectral rigidity  are consistent with pre- dictions of RMT (GOE behaviour), i.e. show universal behaviour. This behaviour is statistically the same as the one observed in quantum chaos (obtained from energy level spacing distributions). The implication of these findings is that RMT not only represents well the statistical fluctuation properties of the energy spectrum of chaotic quantum systems, but also those of the length spectrum of chaotic classical systems. Moreover, sta- tistical fluctuations obtained from spectra of action/length matrices clearly distinguish chaotic from integrable systems.
are consistent with pre- dictions of RMT (GOE behaviour), i.e. show universal behaviour. This behaviour is statistically the same as the one observed in quantum chaos (obtained from energy level spacing distributions). The implication of these findings is that RMT not only represents well the statistical fluctuation properties of the energy spectrum of chaotic quantum systems, but also those of the length spectrum of chaotic classical systems. Moreover, sta- tistical fluctuations obtained from spectra of action/length matrices clearly distinguish chaotic from integrable systems.
2. Length and Action of Trajectories
In classical systems, chaos information is encoded in trajectories. According to the Alekseev-Brudno theorem [38] the temporal length t is related via the Kolmogorov-Sinai K entropy to the information 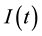 in the segment of trajectory,
in the segment of trajectory,
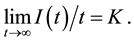 (1)
(1)
This motivates us to look at the length of trajectories and its fluctuation properties. Let 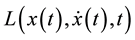 denote the Lagrangian of a system, let
denote the Lagrangian of a system, let 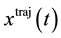 denote a solution (trajectory) of the Euler-Lagrange equations, with boundary points
denote a solution (trajectory) of the Euler-Lagrange equations, with boundary points 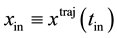 and
and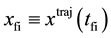 . Let
. Let
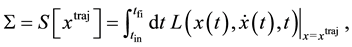 (2)
(2)
denote the action over  and let
and let
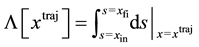 (3)
(3)
denote the length of the trajectory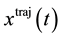 . We choose a finite set of discrete points
. We choose a finite set of discrete points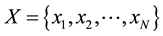 . For all pairs of boundary points
. For all pairs of boundary points![]() , we compute a classical trajectory
, we compute a classical trajectory![]() , connecting those points. We suggest the construction of an action matrix and a length matrix,
, connecting those points. We suggest the construction of an action matrix and a length matrix,
![]()
![]() (4)
(4)
where i and j are respectively the indices of the final and initial boundary points of the trajectory. Both matrices are viable for statistical analysis of classical chaos. In the case of billiard systems, we consider trajectories where the billiard particle moves with constant velocity u and constant kinetic energy E. Then the action and the length matrix are essentially equivalent,
![]() (5)
(5)
Numerical Calculation of Length Matrices
When solving for two boundary points ![]() and
and ![]() in a billiard the solution is generally not unique; the number of possible trajectories varies with the number
in a billiard the solution is generally not unique; the number of possible trajectories varies with the number ![]() of rebounds. We have thus classified trajectories-and corresponding length matrices-according to
of rebounds. We have thus classified trajectories-and corresponding length matrices-according to![]() .
.
For ![]() the number of trajectories is quite large
the number of trajectories is quite large![]() . In order to limit computational cost, we considered smaller subsets of length matrices, in the following way. For a given number of rebounds
. In order to limit computational cost, we considered smaller subsets of length matrices, in the following way. For a given number of rebounds ![]() and a given pair of boundary points
and a given pair of boundary points![]() , we determined the starting angles
, we determined the starting angles ![]() (measured from the normal to the billiard wall at the boundary point) which corresponds to a trajectory
(measured from the normal to the billiard wall at the boundary point) which corresponds to a trajectory![]() . That search was carried out in the
. That search was carried out in the
range![]() . The subsets have been constructed by introducing an upper bound
. The subsets have been constructed by introducing an upper bound ![]() on
on
the number of trajectories and retaining only the trajectories corresponding to the starting angles![]() . We repeated this for all combinations of boundary points. We then checked that this procedure did not spoil the statistical properties we aimed to measure by considering different cutoff
. We repeated this for all combinations of boundary points. We then checked that this procedure did not spoil the statistical properties we aimed to measure by considering different cutoff ![]() and different ordering scheme for the set of trajectories.
and different ordering scheme for the set of trajectories.
3. Integrable Billiard
If one considers integrable quantum systems and analyzes them in terms of the NNS distribution of energy levels and spectral rigidity, then in most cases one finds a Poissonian distribution ![]() which is reflected also in the behaviour of
which is reflected also in the behaviour of![]() . However, there are examples of integrable quantum systems in 2D where the levels are correlated and the level spacing distribution is not given by a Poissonian. Such cases are called non-generic. Berry and Tabor [39] noted as example uncoupled quantum oscillators in 2D. Casati et al. [40] and later Seligman and Verbaarschot [41] showed that also the integrable 2D quantum rectangular incommensurate billiard does not give an uncorrelated Poissonian level spacing distribution. In a recent study of 2D quantum harmonic oscillators Chakrabarti and Hu [42] found in the case of uncoupled oscillators a level spacing distribution displaying a
. However, there are examples of integrable quantum systems in 2D where the levels are correlated and the level spacing distribution is not given by a Poissonian. Such cases are called non-generic. Berry and Tabor [39] noted as example uncoupled quantum oscillators in 2D. Casati et al. [40] and later Seligman and Verbaarschot [41] showed that also the integrable 2D quantum rectangular incommensurate billiard does not give an uncorrelated Poissonian level spacing distribution. In a recent study of 2D quantum harmonic oscillators Chakrabarti and Hu [42] found in the case of uncoupled oscillators a level spacing distribution displaying a ![]() peak plus some background. They measured the spectral correlation via the
peak plus some background. They measured the spectral correlation via the
spectral rigidity ![]() and observed a flat curve for
and observed a flat curve for ![]() saturating at
saturating at![]() . Similar results
. Similar results
were found in the case with weak harmonic coupling, yielding ![]() and correlation
and correlation![]() . This behaviour is similar to the rigidity of a picket fence (Dirac comb) of equally spaced levels with
. This behaviour is similar to the rigidity of a picket fence (Dirac comb) of equally spaced levels with![]() . They conclude that the 2D quantum oscillator system is highly correlated at short and long- range, is regular and very rigid.
. They conclude that the 2D quantum oscillator system is highly correlated at short and long- range, is regular and very rigid.
Laprise et al. [36] considered the classical integrable circular billiard and constructed a length matrix from classical trajectories between boundary points located evenly on the billiard wall. They found saturation in the spectral rigidity for large L at ![]() which behaves like the rigidity of a Dirac comb
which behaves like the rigidity of a Dirac comb![]() . In conjunction with a correlation coefficient of
. In conjunction with a correlation coefficient of ![]() and a level spacing distribution
and a level spacing distribution ![]() (Dirac comb) this indicates high correlation at short and long range and very rigid behaviour.
(Dirac comb) this indicates high correlation at short and long range and very rigid behaviour.
Rectangular Billiard
As example of an integrable classical billiard we consider the 2D rectangular billiard, shown in Figure 1.
The shape is determined by the parameters a, b, which were chosen to be ![]() and
and![]() . The boundary points
. The boundary points![]() , located in the upper right quarter of the billiard wall, are distributed regularly, with perimeter spacing given by
, located in the upper right quarter of the billiard wall, are distributed regularly, with perimeter spacing given by
![]() (6)
(6)
For a given pair of boundary points, we found that the behaviour of the number of trajectories versus the number of rebounds is linear (not shown). The error behaviour of trajectories as a function of the number of rebounds has been obtained by taking into account ![]() trajectories corresponding to different initial conditions. The error was stable in the regime
trajectories corresponding to different initial conditions. The error was stable in the regime ![]() and did not increase beyond
and did not increase beyond![]() . This is in contrast to an exponential increase found in chaotic billiards.
. This is in contrast to an exponential increase found in chaotic billiards.
The symmetry of the rectangular billiard is mirror symmetry under reflection about the x- and y-axes (with origin at centre of rectangle). The symmetry shows up in the shape of trajectories. For example, a trajectory (1) going from starting point ![]() to endpoint
to endpoint ![]() bouncing once from the lower boundary wall has the same shape as the trajectory (2) going from starting point
bouncing once from the lower boundary wall has the same shape as the trajectory (2) going from starting point ![]() to endpoint
to endpoint ![]() bouncing once from the lower boundary wall. Trajectory (2) is obtained by a translation of trajectory (1) in x-direction by the amount of perimeter spacing, Equation (6). However, such discrete translations do not form a group (they would form a group if one would consider the rectangular billiard with periodic boundary conditions at all billiard boundary walls, which would map the billiard on a torus, and the symmetry group would then be a rotation group). The length matrix is not exactly a circular matrix either, however, it shares with circular matrices the property of having a number of different matrix elements equal to or less than the rank of the matrix. This property implies strong correlations between length matrix elements, which translates to strong correlations of eigenvalues of the length matrix. To sum up, although there is no exact symmetry group, there are residues of a “broken symmetry
bouncing once from the lower boundary wall. Trajectory (2) is obtained by a translation of trajectory (1) in x-direction by the amount of perimeter spacing, Equation (6). However, such discrete translations do not form a group (they would form a group if one would consider the rectangular billiard with periodic boundary conditions at all billiard boundary walls, which would map the billiard on a torus, and the symmetry group would then be a rotation group). The length matrix is not exactly a circular matrix either, however, it shares with circular matrices the property of having a number of different matrix elements equal to or less than the rank of the matrix. This property implies strong correlations between length matrix elements, which translates to strong correlations of eigenvalues of the length matrix. To sum up, although there is no exact symmetry group, there are residues of a “broken symmetry
![]()
Figure 1. 2D Rectangular billiard. Horizontal length a, vertical length b. Trajectories go from boundary points ![]() to
to ![]() lo- cated in the upper right quarter of the billiard wall.
lo- cated in the upper right quarter of the billiard wall.
group of discrete translations,” which imply strong correlations among length matrix elements and among eigenvalues of the length matrix. We expect that this will manifest itself in the statistical behaviour in the level spacing distribution ![]() and the spectral rigidity
and the spectral rigidity![]() . The results corresponding to the parameters
. The results corresponding to the parameters ![]() and
and ![]() are shown in Figure 2. Figure 2(a) represents the distribution
are shown in Figure 2. Figure 2(a) represents the distribution ![]() of length matrix elements. Its shape looks quite different from the near-Gaussian shape for chaotic billiards (see below). Figure 2(b) shows the spectral rigidity
of length matrix elements. Its shape looks quite different from the near-Gaussian shape for chaotic billiards (see below). Figure 2(b) shows the spectral rigidity ![]() of the spectrum of the length matrix. It rapidly saturates to a value
of the spectrum of the length matrix. It rapidly saturates to a value
![]() , which is close to the value
, which is close to the value ![]() of an ideal Dirac comb. We have also
of an ideal Dirac comb. We have also
computed the correlation coefficient to obtain![]() . This is consistent also with the NNS level distribution
. This is consistent also with the NNS level distribution ![]() of the length matrix shown in Figure 2(c) where one observes
of the length matrix shown in Figure 2(c) where one observes ![]() indicating the behaviour of a Dirac comb. The rectangular billiard turns out to be highly correlated at short and long range, to be very rigid and to be regular.
indicating the behaviour of a Dirac comb. The rectangular billiard turns out to be highly correlated at short and long range, to be very rigid and to be regular.
This is possibly evidence for universal behaviour in the integrable case. Comparing the behaviour of the rectangular billiard with the circular billiard [36] , we observe that they differ in their symmetry properties. In the circular billiard hopping from one boundary point to its neighbour stands for a group operation. The corre- sponding operation in the rectangular billiard has no group property. However, the resulting strong correlation and spectral rigidity are found to be very similar for both billiards.
4. Chaotic Billiards
4.1. Sinai Billiard
For general closed 2D billiards, the mean free path length ![]() in between two collisions is given by the billiard geometry via [43]
in between two collisions is given by the billiard geometry via [43]
![]() (7)
(7)
where ![]() stands for the billiard area and
stands for the billiard area and ![]() for the length of the wall. Let us now consider a particle of mass m moving in the 2D Sinai billiard (see Figure 3(a)). The classical Sinai billiard system is known to be fully chaotic [44] . The billiard is symmetric under mirror operation about x- and y-axes, and about the diagonals of angles
for the length of the wall. Let us now consider a particle of mass m moving in the 2D Sinai billiard (see Figure 3(a)). The classical Sinai billiard system is known to be fully chaotic [44] . The billiard is symmetric under mirror operation about x- and y-axes, and about the diagonals of angles ![]() and
and![]() , respectively, passing through the centre. In order not to mix different symmetry classes, we consider the billiard with boundary points
, respectively, passing through the centre. In order not to mix different symmetry classes, we consider the billiard with boundary points ![]() located in one eighth of the exterior billiard wall (see Figure 3(a)). It is important to make sure that the chaotic behaviour comes from the dynamics of the system and not from random location of boundary points. Thus we have located the boundary points in a regular way, with perimeter spacing
located in one eighth of the exterior billiard wall (see Figure 3(a)). It is important to make sure that the chaotic behaviour comes from the dynamics of the system and not from random location of boundary points. Thus we have located the boundary points in a regular way, with perimeter spacing
![]() (8)
(8)
The rule of dynamics is free motion in the interior region and elastic specular collision at the central disc and the exterior square wall. We have classified trajectories using the scheme presented in Section 2. A global
characteristic feature of chaos is encoded in the number of classical trajectories. For the Sinai billiard we found that the number ![]() of trajectories averaged over all pairs of boundary points increases as function of the number of rebounds
of trajectories averaged over all pairs of boundary points increases as function of the number of rebounds ![]() like an exponential,
like an exponential,
![]() (9)
(9)
Such exponential behaviour in chaotic billiards is clearly distinct from the behaviour in integrable billiards, where the number of trajectories increases linearly with the number of rebounds (see rectangular billiard). We
fixed a value for ![]() and then generated an ensemble of length matrices
and then generated an ensemble of length matrices ![]() corresponding
corresponding
to all possible trajectory indices![]() . In general one expects that chaotic behaviour develops with increasing
. In general one expects that chaotic behaviour develops with increasing![]() .
.
In order to make sure that the chaotic behaviour is not due to numerical noise, we estimated the numerical error ![]() by following a trajectory from a given starting point
by following a trajectory from a given starting point ![]() until it carried out
until it carried out ![]() rebounds, then following the trajectory in time reversed direction to arrive after another
rebounds, then following the trajectory in time reversed direction to arrive after another ![]() at some
at some![]() . We observed that the error behaviour has two regimes. For
. We observed that the error behaviour has two regimes. For ![]() it shows an exponential increase, following on average the rule
it shows an exponential increase, following on average the rule
![]() (10)
(10)
For ![]() saturation is reached (the relative error is in the order of one). Such exponential behaviour (see Figure 3(b)) is related to the largest positive Lyapunov exponent of the system and thus represents a global characteristic of a chaotic system. Like the exponential behaviour of number of trajectories, Equation (9), also the exponential error behaviour distinguishes between chaotic billiards and integrable billiards.
saturation is reached (the relative error is in the order of one). Such exponential behaviour (see Figure 3(b)) is related to the largest positive Lyapunov exponent of the system and thus represents a global characteristic of a chaotic system. Like the exponential behaviour of number of trajectories, Equation (9), also the exponential error behaviour distinguishes between chaotic billiards and integrable billiards.
We found a relative error of about ![]() for
for![]() . After unfolding the spectra we retain 8 significant digits. We used the technique of Gaussian broadening [13] [45] to unfold the raw spectrum. In this method there is a free parameter, which we tuned to reproduce the auto-correlation coefficient (
. After unfolding the spectra we retain 8 significant digits. We used the technique of Gaussian broadening [13] [45] to unfold the raw spectrum. In this method there is a free parameter, which we tuned to reproduce the auto-correlation coefficient (![]() for Wigner distribution [8] [46] ). For a given trajectory index
for Wigner distribution [8] [46] ). For a given trajectory index ![]() we computed a level spacing distribution. Afterwards we superimposed the spectra corresponding to different trajectory indices
we computed a level spacing distribution. Afterwards we superimposed the spectra corresponding to different trajectory indices![]() . For
. For ![]() the number of trajectories is quite large
the number of trajectories is quite large![]() . In order to limit computational cost, we have restricted ourselves by considering smaller subsets of length matrices. It turns out that
. In order to limit computational cost, we have restricted ourselves by considering smaller subsets of length matrices. It turns out that ![]() gives a reasonably good statistics. Note that, in this way, we don’t consider all trajectories and have to order them arbitrarily as explained in Section 2. Therefore, we verified that the resulting distributions are independent of the particular subset of trajectories and ordering used within statistical errors. The resulting level spacing distribution
gives a reasonably good statistics. Note that, in this way, we don’t consider all trajectories and have to order them arbitrarily as explained in Section 2. Therefore, we verified that the resulting distributions are independent of the particular subset of trajectories and ordering used within statistical errors. The resulting level spacing distribution ![]() of length eigenvalues and the spectral rigidity
of length eigenvalues and the spectral rigidity![]() , corresponding to
, corresponding to ![]() boundary points,
boundary points, ![]() rebounds and
rebounds and ![]() trajectories, are shown in Figure 4(b) & Figure 4(c). The results show a Wigner distribution for
trajectories, are shown in Figure 4(b) & Figure 4(c). The results show a Wigner distribution for![]() , and are consistent with GOE behaviour also for
, and are consistent with GOE behaviour also for![]() . As in the quantum Sinai billiard, the level spacing distribution has been shown to give a Wigner distribution [7] .
. As in the quantum Sinai billiard, the level spacing distribution has been shown to give a Wigner distribution [7] .
The histogram of the length matrix elements itself is shown in Figure 4(a). The distribution looks close to a Gaussian. Determining if it is a pure Gaussian, is a question physically relevant for the following reason: If the distribution ![]() is a Gaussian, then the matrix elements obey GOE statistics. Then RMT [6] implies that the level fluctuation statistics
is a Gaussian, then the matrix elements obey GOE statistics. Then RMT [6] implies that the level fluctuation statistics ![]() and the spectral rigidity
and the spectral rigidity ![]() follow GOE statistics (which seems consistent with the numerical results shown in Figure 4(b) & Figure 4(c). We pointed out above that the random walk model gives a Gaussian distribution for the histogram of the length matrix elements
follow GOE statistics (which seems consistent with the numerical results shown in Figure 4(b) & Figure 4(c). We pointed out above that the random walk model gives a Gaussian distribution for the histogram of the length matrix elements![]() . The random walk model is mathematically a Markov chain, i.e., the length of each piece of straight path in between subsequent collisions is given by a random number. Two subsequent random numbers are statistically inde- pendent. On the other hand, the chaotic Sinai billiard is a deterministic system, and the length of two subsequent pieces of straight trajectory are not independent. Hence it is plausible that the distribution
. The random walk model is mathematically a Markov chain, i.e., the length of each piece of straight path in between subsequent collisions is given by a random number. Two subsequent random numbers are statistically inde- pendent. On the other hand, the chaotic Sinai billiard is a deterministic system, and the length of two subsequent pieces of straight trajectory are not independent. Hence it is plausible that the distribution ![]() of length matrix elements for the Sinai billiard is not given by an exact Gaussian.
of length matrix elements for the Sinai billiard is not given by an exact Gaussian.
Mathematical note. The BGS-conjecture does not state that the matrix elements of a quantum Hamiltonian must be distributed like a GOE ensemble. The conjecture rather only says that the statistical fluctuations of the eigenvalue spacings obtained from the quantum Hamiltonian are the same as those from a GOE ensemble, giving a Wignerian distribution. In other words, it is possible that the matrix elements of the quantum Hamil- tonian be distributed quite differently from a Gaussian and that its level spacing distribution be nevertheless Wignerian.
Such a situation, where the distribution of matrix elements is not GOE, but the level fluctuation statistics is GOE, occurs in nuclear physics. An example is the distribution of the Hamiltonian matrix elements obtained from nuclear shell model calculations [12] . In this model, there are vanishing Hamiltonian matrix elements. This implies that the number of independent matrix elements is much smaller than in a random matrix of the same size. However, Brody et al. [47] showed that the 2-body residual interaction in the shell model yields matrix elements of random character following a Gaussian distribution. In particular, they showed that spectral fluctuation properties from such ensembles with orthogonal symmetry are identical to those from GOE. That implies that GOE is meaningful to predict spectral fluctuation properties of nuclei governed by 2-body interactions, though the Hamiltanian does not follow a Gaussian distribution.
4.2. Bunimovich Stadium Billiard
Let us consider the 2D Bunimovich stadium billiard with semi-axes a and b (Figure 5). The billiard is known to be fully chaotic [48] [49] . The billiard is symmetric under mirror operation about x- and y-axes. In order not to mix different symmetry classes, we consider the billiard with boundary points ![]() located in one quarter of the billiard wall. The quarter perimeter has the length
located in one quarter of the billiard wall. The quarter perimeter has the length![]() . The nodes
. The nodes ![]() are equidistantly distributed on the quarter perimeter of the stadium, with perimeter spacing given by
are equidistantly distributed on the quarter perimeter of the stadium, with perimeter spacing given by
![]() (11)
(11)
The rule of dynamics is free motion in the interior region and elastic specular collision at the exterior square wall. For a given pair of boundary points, the number of trajectories ![]() connecting these points increases on average with the number of rebounds exponentially, according to
connecting these points increases on average with the number of rebounds exponentially, according to
![]() (12)
(12)
Such behaviour is qualitatively similar to that found in the Sinai billiard. We also measured the numerical
![]()
Figure 5. 2D stadium billiard. Trajectories go from boundary points ![]() to
to ![]() located in a segment of one quarter of the billiard wall.
located in a segment of one quarter of the billiard wall.
error following the method used in the Sinai billiard. Likewise, we found a regime of exponential behaviour followed by a regime of saturation (not shown). On average the exponential increase is given by
![]() (13)
(13)
We have classified trajectories by the the number of rebounds![]() , which was kept fixed. In this way, we
, which was kept fixed. In this way, we
generate an ensemble of length matrices ![]() corresponding to all possible trajectory indices
corresponding to all possible trajectory indices![]() .
.
For each trajectory index ![]() we computed a level spacing distribution. Afterwards we superimposed the spectra coming from a smaller subset of trajectory indices
we computed a level spacing distribution. Afterwards we superimposed the spectra coming from a smaller subset of trajectory indices ![]() (like we did for the Sinai billiard). The resulting level spacing distribution
(like we did for the Sinai billiard). The resulting level spacing distribution ![]() of length eigenvalues and the spectral rigidity
of length eigenvalues and the spectral rigidity ![]() are shown in Figure 6(b) & Figure 6(c). The results are consistent with a Wigner distribution, i.e. GOE behaviour. The histogram of the length matrix elements
are shown in Figure 6(b) & Figure 6(c). The results are consistent with a Wigner distribution, i.e. GOE behaviour. The histogram of the length matrix elements ![]() shown in Figure 6(a) looks close to a Gaussian.
shown in Figure 6(a) looks close to a Gaussian.
In order to see if the observed Wigner distribution in the level spacing distribution depends on the statistical method of averaging over several trajectories (i.e. length matrices![]() ) we have tested an alternative, where we averaged over different stadium geometries. All stadium billiards are fully chaotic, and if the Wigner behaviour is universal, this should show up for any stadium geometry. Superimposing spectra corresponding to different stadium shapes should improve statistics. In their paper on quantum chaos in nuclear physics, Bohigas et al. [50] have analyzed spectra of a series of different heavy nuclei (but having the same quantum numbers) and showed that their level fluctuation statistics agrees with the prediction of RMT. These different nuclei correspond to different potentials. In analogy to that we considered here length spectra corresponding to different stadium shapes. The stadium wall represents a curve where the potential jumps from zero to infinity. Hence different stadium shapes correspond to different potentials. By superimposing spectra from different stadium shapes we obtained results displayed in Figure 7. Within statistical errors the results are equivalent to those obtained by superimposing spectra from different trajectories (Figure 6).
) we have tested an alternative, where we averaged over different stadium geometries. All stadium billiards are fully chaotic, and if the Wigner behaviour is universal, this should show up for any stadium geometry. Superimposing spectra corresponding to different stadium shapes should improve statistics. In their paper on quantum chaos in nuclear physics, Bohigas et al. [50] have analyzed spectra of a series of different heavy nuclei (but having the same quantum numbers) and showed that their level fluctuation statistics agrees with the prediction of RMT. These different nuclei correspond to different potentials. In analogy to that we considered here length spectra corresponding to different stadium shapes. The stadium wall represents a curve where the potential jumps from zero to infinity. Hence different stadium shapes correspond to different potentials. By superimposing spectra from different stadium shapes we obtained results displayed in Figure 7. Within statistical errors the results are equivalent to those obtained by superimposing spectra from different trajectories (Figure 6).
5. Universality in Chaotic Billiards
The numerical experiments with chaotic billiards investigated above led us to the following observations: 1) For a given pair of boundary points![]() , the number of classical trajectories
, the number of classical trajectories ![]() shows exponential behaviour as function of
shows exponential behaviour as function of![]() . 2) For a given pair of boundary points, the numerical error
. 2) For a given pair of boundary points, the numerical error ![]() shows exponential behaviour as function of the number of rebounds
shows exponential behaviour as function of the number of rebounds![]() . 3) The NNS level fluctuation distribution
. 3) The NNS level fluctuation distribution ![]() obtained from eigenvalues of the length matrix
obtained from eigenvalues of the length matrix ![]() shows a Wignerian distribution. This is consistent with GOE behaviour predicted by RMT. 4) The spectral rigidity
shows a Wignerian distribution. This is consistent with GOE behaviour predicted by RMT. 4) The spectral rigidity ![]() obtained from the spectrum of length matrix
obtained from the spectrum of length matrix ![]() is also found consistent with GOE behaviour predicted by RMT. 5) The distribution
is also found consistent with GOE behaviour predicted by RMT. 5) The distribution ![]() of length matrix elements
of length matrix elements ![]() is found to be close to a Gaussian.
is found to be close to a Gaussian.
The leading Gaussian behaviour in the distribtion ![]() is possibly universal. How can we understand such behaviour of
is possibly universal. How can we understand such behaviour of ![]() in chaotic billiards? The Sinai billiard is equivalent to a system where the billiard ball moves in an open system of equal spherical discs located on a 2D rectangular regular grid, known as the 2D (diluted) Lorentz gas model. The billiard ball alternates between free motion and collisions with the circular
in chaotic billiards? The Sinai billiard is equivalent to a system where the billiard ball moves in an open system of equal spherical discs located on a 2D rectangular regular grid, known as the 2D (diluted) Lorentz gas model. The billiard ball alternates between free motion and collisions with the circular
discs. There are two types of 2D periodic Lorentz gases (or Sinai billiards on a torus): One has a finite horizon, where free paths between collisions are bounded (the scatterers are sufficiently dense to block every direction of motion. The other type has an infinite horizon, where the particle can move indefinitely without collision with
any disc. The Sinai billiard investigated above (see Figure 3(a)) belongs to this class. The CLT, the existence of finite diffusion coefficient and the convergence to Brownian motion were proven only for the periodic Lorentz gas with finite horizon [21] [23] . In the case of infinite horizon, the CLT has not been proven. Moreover, in this case the diffusion coefficient is infinite and there is no convergence to Brownian motion [51] .
Actually, for the periodic Lorentz gas with finite horizon it can be shown rigorously that the distribution of length of trajectories becomes a Gaussian distribution in the limit of many bounces. This holds when the initial points of trajectories are distributed randomly on the billiard boundary. Then Chernov and Markarian [52] prove the following result
![]() (14)
(14)
for all![]() . Here
. Here ![]() denotes the return function and
denotes the return function and
![]() (15)
(15)
is the time of the n-th collision. ![]() is the variance of the random variable depending on the observable f, which here is the return function
is the variance of the random variable depending on the observable f, which here is the return function![]() .
. ![]() is the collision map and M is the collision space (phase space of billiard map). Thus the distribution of the travel time until the n-th collision obeys the CLT, and hence converges in distribution to a normal, i.e. Gaussian distribution in the limit where the number of collisions goes to infinity. In the case where the billiard particle moves with constant speed u, this means also the length of trajectory
is the collision map and M is the collision space (phase space of billiard map). Thus the distribution of the travel time until the n-th collision obeys the CLT, and hence converges in distribution to a normal, i.e. Gaussian distribution in the limit where the number of collisions goes to infinity. In the case where the billiard particle moves with constant speed u, this means also the length of trajectory ![]() obeys the CLT, and the length distribution
obeys the CLT, and the length distribution ![]() tends to a normal Gaussian dis- tribution for
tends to a normal Gaussian dis- tribution for![]() .
.
This result seems to support our numerical findings of a (near) Gaussian distribution of length of trajectories. However, the scenario where the above mathematical result holds and the scenario of our numerical study differ in two respects, namely in the distribution of boundary points and in the horizon of billiard. For the purpose of statistical analysis in terms of RMT we are interested in the distribution![]() , which corresponds to the case where the billiard particle starts from and arrives at boundary positions taken from a discrete set of boundary points, which is different from an initial random set of boundary points. Nevertheless, it seems plausible that a similar mathematical result may hold also for the discrete set of initial and final boundary points, such that
, which corresponds to the case where the billiard particle starts from and arrives at boundary positions taken from a discrete set of boundary points, which is different from an initial random set of boundary points. Nevertheless, it seems plausible that a similar mathematical result may hold also for the discrete set of initial and final boundary points, such that ![]() tends to a Gaussian. Second, the mathematical result holds for the case of finite horizon, while the Sinai billiard in our numerical study has an infinite horizon. At a first glance, it looks puzzling in absence of strong mathematical results (for infinite horizon) that our numerical results nevertheless show (near) Gaussian behaviour for the length distribution. A possible explanation is this: The choice of the discrete set of regularly distributed boundary points selects preferentially trajectories which often bounce at the central disc, while trajectories with infinite horizon (no bounces at disc) are avoided. This is supported also by numerical evidence that the distribution
tends to a Gaussian. Second, the mathematical result holds for the case of finite horizon, while the Sinai billiard in our numerical study has an infinite horizon. At a first glance, it looks puzzling in absence of strong mathematical results (for infinite horizon) that our numerical results nevertheless show (near) Gaussian behaviour for the length distribution. A possible explanation is this: The choice of the discrete set of regularly distributed boundary points selects preferentially trajectories which often bounce at the central disc, while trajectories with infinite horizon (no bounces at disc) are avoided. This is supported also by numerical evidence that the distribution ![]() of the Sinai billiard (Figure 4(a)) and that of the rectangular billiard viewed as Sinai billiard with central disc of radius zero (Figure 2(a)) are quite different.
of the Sinai billiard (Figure 4(a)) and that of the rectangular billiard viewed as Sinai billiard with central disc of radius zero (Figure 2(a)) are quite different.
In the case of the stadium billiard, Bálint and Gouëzel [53] have shown that a limit theorem also holds. They proved that the limit distribution ![]() is Gaussian, however, the scaling factor is not given by the standard expression
is Gaussian, however, the scaling factor is not given by the standard expression![]() , but rather by
, but rather by![]() . As consequence, there is no finite standard diffusion coefficient and no convergence to Brownian motion. Bálint and Gouëzel prove that the distribution of length of trajectories, tends to a gaussian distribution in the limit where the number of collisions n goes to infinity. Like in the Lorentz gas, this corresponds to a random distribution of initial points on the boundary. This is consistent with our numerical results of the stadium billiard which show in
. As consequence, there is no finite standard diffusion coefficient and no convergence to Brownian motion. Bálint and Gouëzel prove that the distribution of length of trajectories, tends to a gaussian distribution in the limit where the number of collisions n goes to infinity. Like in the Lorentz gas, this corresponds to a random distribution of initial points on the boundary. This is consistent with our numerical results of the stadium billiard which show in ![]() small deviations from a Gaussian comparable in magnitude with those in the Sinai model. They are likely due to the small number of bounces.
small deviations from a Gaussian comparable in magnitude with those in the Sinai model. They are likely due to the small number of bounces.
Let us suppose that ![]() does tend to a Gaussian. As a consequence, in this limit (and after suitable normalization) the length matrix
does tend to a Gaussian. As a consequence, in this limit (and after suitable normalization) the length matrix ![]() itself will become a GOE matrix [11] . This is sufficient to guarantee in this limit that the level fluctuations
itself will become a GOE matrix [11] . This is sufficient to guarantee in this limit that the level fluctuations ![]() and spectral rigidity
and spectral rigidity ![]() obtained from the matrix
obtained from the matrix ![]() show GOE behaviour [6] . This does establish universal behaviour in the limit of many bounces in the case of the rectangular Lorentz gas/Sinai billiard as well as the Bunimovich stadium billiard.
show GOE behaviour [6] . This does establish universal behaviour in the limit of many bounces in the case of the rectangular Lorentz gas/Sinai billiard as well as the Bunimovich stadium billiard.
Now we want to address the following questions:
1) Concerning universality observed in classical chaotic billiards, what are the underlying physical principles? We will give a heuristic description-not a rigorous derivation-of the physical principles leading to the pheno- menon of universality. Let us consider chaotic billiards in the regime of macroscopic times, i.e., when the billiard particle does a large number of bounces. Consider a trajectory carrying out ![]() bounces. Because the system is a classically deterministic system, each segment of trajectory between two subsequent bounces depends on and is completely determined by the preceeding segment of trajectory. However, if one computes the correlator between trajectory segment n and trajectory segment
bounces. Because the system is a classically deterministic system, each segment of trajectory between two subsequent bounces depends on and is completely determined by the preceeding segment of trajectory. However, if one computes the correlator between trajectory segment n and trajectory segment![]() , such correlation tends to zero, when k becomes large (see below equations (16) and (17), and reference [52] ). This effect is due to the dynamics of classical chaos (positive Lyapunov exponent). Thus two segments of the same trajectory, which are sufficiently distant in terms of travel time or number of intermediate bounces, will become statistically independent. This makes the system similar to a random walk system, where any two segments of a trajectory are statistically independent. To see this, consider trajectories of the chaotic billiard composed of N segments (
, such correlation tends to zero, when k becomes large (see below equations (16) and (17), and reference [52] ). This effect is due to the dynamics of classical chaos (positive Lyapunov exponent). Thus two segments of the same trajectory, which are sufficiently distant in terms of travel time or number of intermediate bounces, will become statistically independent. This makes the system similar to a random walk system, where any two segments of a trajectory are statistically independent. To see this, consider trajectories of the chaotic billiard composed of N segments (![]() bounces), and choose
bounces), and choose![]() . Then we can consider all segments
. Then we can consider all segments ![]() with
with ![]() to be statistically independent. Consequently, for
to be statistically independent. Consequently, for ![]() almost all segments are statistically independent from each other and hence the system will statistically behave similar to a random walk system. This means in the regime of a large number of rebounds that the system looses its memory of the detailed underlying laws of physics. It becomes universal. Such universality manifests itself in the statistical observable of distribution of length of trajecories
almost all segments are statistically independent from each other and hence the system will statistically behave similar to a random walk system. This means in the regime of a large number of rebounds that the system looses its memory of the detailed underlying laws of physics. It becomes universal. Such universality manifests itself in the statistical observable of distribution of length of trajecories ![]() which for all chaotic billiards studied here shows a near-Gaussian character (like the random walk system).
which for all chaotic billiards studied here shows a near-Gaussian character (like the random walk system).
2) What is the physical significance of such universality? If one considers classically chaotic billiards in the regime of macroscopic times, where ![]() denotes the matrix of length of trajectories, and if one considers as statistical observable the distribution of length of trajectories
denotes the matrix of length of trajectories, and if one considers as statistical observable the distribution of length of trajectories![]() , then
, then ![]() will asymptotically approach a Gaussian and
will asymptotically approach a Gaussian and ![]() will asymptotically become a random matrix from a Gaussian Orthogonal Ensemble (GOE). Hence the level spacing distribution of the length matrix
will asymptotically become a random matrix from a Gaussian Orthogonal Ensemble (GOE). Hence the level spacing distribution of the length matrix ![]() will be described by GOE random matrix statistics. However, one should be careful. The matrix of length
will be described by GOE random matrix statistics. However, one should be careful. The matrix of length ![]() has not lost all information on the physics of the underlying system. For instance, the variance of length
has not lost all information on the physics of the underlying system. For instance, the variance of length ![]() turns out to behave differently in the Sinai billiard (on a torus) in the finite horizon regime, scaling like n, in contrast to the stadium billiard, where it scales like
turns out to behave differently in the Sinai billiard (on a torus) in the finite horizon regime, scaling like n, in contrast to the stadium billiard, where it scales like![]() . Statistical behaviour depends on the particular observable considered. Thus using the length marix
. Statistical behaviour depends on the particular observable considered. Thus using the length marix![]() , which via
, which via ![]() and
and ![]() displays universal behaviour, we can compute physical observables, e.g., being related to
displays universal behaviour, we can compute physical observables, e.g., being related to![]() . Such observable yields transport properties, in particular the diffusion coefficient. Results of transport properties are presented in Section 6.
. Such observable yields transport properties, in particular the diffusion coefficient. Results of transport properties are presented in Section 6.
3) Are there connections between universality and physical quantities which are easily observed in real systems? In particular, is such universality related to transport properties of the classical system? The answer is yes, and we will show in Section 6 how a transport coefficient can be obtained from the length matrix ![]() in the regime of universality.
in the regime of universality.
Moreover, the behaviour of the chaotic billiard systems when approaching the regime of universality is characterized by laws specific for the particular billiard system. As example consider the decay laws of correla- tion functions. Consider a billiard trajectory and consider as observable f the segment of trajectory from n to![]() , while g denotes the segment from
, while g denotes the segment from ![]() to
to![]() . Then the correlation function between observables f and g for many billiards shows either an exponential fall-off behaviour [52]
. Then the correlation function between observables f and g for many billiards shows either an exponential fall-off behaviour [52]
![]() (16)
(16)
or polynomial fall off behaviour
![]() (17)
(17)
where A and B are constants, ![]() and the exponent
and the exponent ![]() is specific for the particular billiard. For example, the triangular Lorentz gas as well as the Bunimovich stadium billiard obey exponential falloff behaviour [52] .
is specific for the particular billiard. For example, the triangular Lorentz gas as well as the Bunimovich stadium billiard obey exponential falloff behaviour [52] .
Here we suggest for chaotic billiard systems that the approach towards universality (i.e., increasing the number of rebounds) contains further physical information characteristic for the system. In particular, we expect that the distribution ![]() approaches a Gaussian,
approaches a Gaussian,
![]() (18)
(18)
for![]() , where the asymptotic approach is characterized by an exponent characteristic for the particular billiard.
, where the asymptotic approach is characterized by an exponent characteristic for the particular billiard.
4) Are those universality properties related to thermodynamical observables? If we consider the chaotic billiards consisting of a single particle moving in a rigid environment of scatterers, then it does not make sense to talk about thermodynamics. Thus for systems considered in this work the answer is no. However, if one considers billiards of many particles, then thermodynamics (as a function of temperature) will influence the dynamics. We shall defer the study of such effects on universality to future work.
5) Is such universality related to spectral statistics of the corresponding quantum system, i.e., what is the relation between universality in classical chaotic systems and universality in chaotic quantum systems, as defined via the Bohigas-Giannoni-Schmit conjecture [7] ? This is a very interesting question, for which we do not have an answer. The finding that universality properties exist in both, classical and quantum chaos, may be a hint that such a relation actually exists. On the other hand, for universality in quantum chaos in the semi- classical regime, periodic orbits play a crucial role (via Gutzwillers trace formula). In contrast, in our study of chaotic classical billiards universality is captured in the length matrix of bouncing, zig-zag, non-periodic trajectories. In order to address such question further, we suggest to consider the path integral relation (in Euclidean, i.e. imaginary time)
![]() (19)
(19)
which relates the quantum Hamltonian H to the classical Euclidean action![]() . For billiards, recall that the length of a trajectory is essentially equivalent to its action. Thus spectral properties of the quantum Hamiltonian may indeed be related to the spectrum of the classical action.
. For billiards, recall that the length of a trajectory is essentially equivalent to its action. Thus spectral properties of the quantum Hamiltonian may indeed be related to the spectrum of the classical action.
6. Transport Properties from Length of Trajectories
Above we have shown for the Bunimovich stadium billiard and for the Sinai billiard that they display universality properties via the statistical behaviour of the matrix of length of trajectories. Here we will show that such universal behaviour is related to relevant physical quantities. In particular we will extract transport properties from the length matrix (note the analogy to computation of transport properties in quantum chaos in semi-classical regime via Gutzwiller formula). As examples we consider the stadium billiard.
In systems for which the CLT is verified, the diffusive character is manifested by a linear relation between the time of travel and the variance of position. The diffusion coefficient d (in 2 dimensions) is given by the Einstein relation
![]() (20)
(20)
where ![]() denotes the time of travel and
denotes the time of travel and ![]() denotes the variance of the position. A similar linear relation between the time of travel and the variance of the length of trajecories can be demonstrated for the periodic triangular Lorentz gas with finite horizon, verifying the CLT (results not shown here):
denotes the variance of the position. A similar linear relation between the time of travel and the variance of the length of trajecories can be demonstrated for the periodic triangular Lorentz gas with finite horizon, verifying the CLT (results not shown here):
![]() (21)
(21)
where travel time ![]() is related to mean trajectory length of n collisions
is related to mean trajectory length of n collisions ![]() and velocity u via
and velocity u via![]() .
.
Based on this approach, we define a diffusion coefficient with respect to the variable![]() :
:
![]() (22)
(22)
for the Bunmovich stadium billiard, which is a chaotic system with concave repeller/scatterer. We have chosen to analyze such system, and compute its transport properties because it reveals a very interesting non-standard diffusion behaviour. In a numerical modelling study of the stadium billiard, Borgognoni et al. [54] have studied its diffusion behaviour by testing if a linear relation holds between the time of travel and the variance of angular momentum. They found that a linear relation fits quite well their data and computed the diffusion coefficients as ratio of variance of angular momentum and time of travel (or number of bounces). However, in 2006, Bálint and Gouëzel [53] proved rigorously for the stadium billiard that a “non-standard” limit theorem holds, where the width does not follow the usual ![]() as in Equation (22), but rather follows an anomal
as in Equation (22), but rather follows an anomal ![]() law. As consequence, the system does not converge to Brownian motion in the limit of many bounces, and the standard diffusion coefficient does not exist.
law. As consequence, the system does not converge to Brownian motion in the limit of many bounces, and the standard diffusion coefficient does not exist.
We carried out numerical simulations using trajectories of the length matrix ![]() and calculated the total time of travel
and calculated the total time of travel ![]() and the variance of length
and the variance of length![]() . According to reference [53] , one expects that the variance should scale like the travel time with a logarithmic correction
. According to reference [53] , one expects that the variance should scale like the travel time with a logarithmic correction
![]() (23)
(23)
We define the diffusion coefficient by
![]() (24)
(24)
We have done statistical tests of ![]() comparing a fit linear in n with a fit linear in
comparing a fit linear in n with a fit linear in![]() . The results are shown in Figure 8. Making fits of the form
. The results are shown in Figure 8. Making fits of the form
![]()
![]() (25)
(25)
we obtained for the linear fit ![]() with an error of 2.8 (max) and
with an error of 2.8 (max) and ![]() (mean) shown in
(mean) shown in
Figure 8(a), compared to the fit with logarithmic correction giving ![]() with an error of
with an error of ![]() (max) and
(max) and ![]() (mean) shown in Figure 8(b). One observes that the statistical error of the fit including the logarithmic correction is smaller than that of the linear fit. An estimate of the anomalous diffusion constant from the logarithmic fit is shown in Figure 8(c). This means 1) numerical consistance with the mathe- matical result obtained by Bálint and Gouëzel [53] , 2) the Bunimovich stadium billiard, although considered a non-generic billiard in quantum chaos due to the “bouncing ball states” of wave solutions, is a very interesting system in classical chaos in the asymptotic regime of many bounces, which displays anomalous diffusion behaviour, 3) the length matrix
(mean) shown in Figure 8(b). One observes that the statistical error of the fit including the logarithmic correction is smaller than that of the linear fit. An estimate of the anomalous diffusion constant from the logarithmic fit is shown in Figure 8(c). This means 1) numerical consistance with the mathe- matical result obtained by Bálint and Gouëzel [53] , 2) the Bunimovich stadium billiard, although considered a non-generic billiard in quantum chaos due to the “bouncing ball states” of wave solutions, is a very interesting system in classical chaos in the asymptotic regime of many bounces, which displays anomalous diffusion behaviour, 3) the length matrix ![]() which generates universal behaviour in
which generates universal behaviour in ![]() and
and![]() , contains infor- mation allowing to distinguish normal diffusion from anomalous diffusion.
, contains infor- mation allowing to distinguish normal diffusion from anomalous diffusion.
7. Summary
This paper is about classical chaos occuring widely in nature, for example in astrophysics, meteorology and dynamics of the atmosphere, fluid and ocean dynamics, climate change, chemical reactions, biology, physiology, neuroscience, or medicine. We have suggested to extend random matrix theory, used in chaotic quantum systems, to classically chaotic and integrable systems. We have studied fully chaotic as well as integrable billiards and used a statistical description based on the length of trajectories to discriminate chaotic versus inte- grable behaviour.
Results:
1) In chaotic billiards (stadium and Sinai billiards), the NNS distribution ![]() as well as
as well as ![]() obtained from the length matrix show GOE behaviour, i.e., they are universal. The implication is that RMT not only models spectral statistical fluctuation properties in chaotic quantum systems, but goes beyond and applies as well to chaotic classical systems.
obtained from the length matrix show GOE behaviour, i.e., they are universal. The implication is that RMT not only models spectral statistical fluctuation properties in chaotic quantum systems, but goes beyond and applies as well to chaotic classical systems.
2) The distribution of length matrix elements ![]() itself is universal to leading order. The difference between the shape of
itself is universal to leading order. The difference between the shape of ![]() and a Gaussian distribution gives a quantitative measure of how much the motion of the billiard ball in a chaotic billiard differs from a random walk.
and a Gaussian distribution gives a quantitative measure of how much the motion of the billiard ball in a chaotic billiard differs from a random walk.
3) For the integrable rectangular billiard we find a correlation coefficient![]() , in spectral rigidity
, in spectral rigidity ![]() and in the NNS distribution
and in the NNS distribution ![]() strong evidence for rigid behaviour and strong correlation between neigh- bour eigenvalues. Such behaviour can be understood from the observation that integrability introduces strong correlations in length matrix elements. This proliferates to the spectra.
strong evidence for rigid behaviour and strong correlation between neigh- bour eigenvalues. Such behaviour can be understood from the observation that integrability introduces strong correlations in length matrix elements. This proliferates to the spectra.
4) In contrast, for integrable quantum systems the NNS distribution generally shows Poissonian behaviour with correlation coefficient ![]() (there are a few exceptions). Thus from the point of view of level spacing distributions, a marked difference shows up between the classical and the quantum world. In our opinion, such difference is due to the group properties/symmetries of classical trajectories.
(there are a few exceptions). Thus from the point of view of level spacing distributions, a marked difference shows up between the classical and the quantum world. In our opinion, such difference is due to the group properties/symmetries of classical trajectories.
Future directions:
1) We plan to do numerical studies to investigate if universality also holds in chaotic potential systems.
2) We hope that our findings may contribute to obtain a unified description of both, quantum and classical chaos, and help understanding why quantum chaos is typically weaker than classical chaos, e.g., via an effective quantum action [55] [56] .
3) The global statistical approach to classical chaos proposed here may help to give insight into the problem of ergodicity breaking in Hamiltonian systems (e.g., dense packing of discs in the Lorentz gas model [27] ).
Acknowledgements
We are thankful to Prof. L. J. Dubé for insightful discussions on chaotic dynamics and to O. Blondeau-Fournier for discussions and his assistance in performing simulations and analyses presented in Section 3.1 and 4.1. H. Kröger is grateful to Prof. Chernov for discussions on central limit theorems in chaotic billiards. This work has been supported by NSERC Canada.