Reliability Analysis of a Redundant Cascade System by Using Markovian Approach

Nalabolu Swathi, Tallapureddy Sumathi Uma Maheswari

Department of Mathematics, Kakatiya University, Warangal, India.

DOI: 10.4236/jamp.2015.37111                

Abstract

In the present work, it is assumed that the n-components are arranged in the hierarchial order. The n-cascade system surviving with loss of m components by k number of attacks is studied; the general equation for the reliability is obtained for the above said system; and the system reliability is computed numerically for 6-cascade system for 2-number of attacks.

Keywords

Cascade System, Redundancy, Reliability, Markov Process, k Attacks

1. Introduction

Reliability of a system is the probability that a system will adequately perform its intended purpose for a given period of time under stated environmental conditions [1] . In some cases system failures occur due to certain type of stresses acting on them. Thus system composed of random strengths will have its strength as random variable and the stress applied on it will also be a random variable. A system fails whenever an applied stress exceeds strength of the system. Probability and reliability were explained by Shooman [2] . The applications of time dependent stress strength models are explained by Schatz R. et al. [3] . Reliability of a n-cascade system with stress attenuation was proposed by Pandit & Sriwastav [4] . Estimation of reliability was explained by William [5] . Raghavachar et al. [6] [7] studied the reliability of a cascade system with normal stress & strength distri- bution and survival function under stress attenuation in cascade reliability. Detailed explanation of mixture distributions is given in [8] . T. S. Uma Maheswari [9] explained reliability of cascade system with normal stress & exponential strength. T. S. Uma Maheswari [10] studied reliability comparison of an n-cascade system with the addition of an n-strength system. T. S. Uma Maheswari [11] explained relaibility of single stress under n- strengths of life distribution. Rekha et al. [12] studied cascade system reliability with rayleigh distribution. In reliability theory, there are lots of real life situations where the concept of mixture distributions can be applied. For example, in life testing experiments, the systems will be failed due to different causes and the times to failure due to different reasons are likely to follow different distributions. Knowledge of these distributions is essential to eliminate cause of failures and thereby to improve the reliability. Maya, T. Nair [13] described the estimation of reliability based on finite mixture of pare to and beta distributions.

Stochastic process is a mathematical model that evolves over time in a probabilistic manner. A special kind of stochastic process is called Markov process, where the outcome of an experiment depends only on the outcome of the previous experiment, i.e., the next state of the system depends only on the present state, not on preceding states. Cascade redundancy is the provision of alternative means or parallel paths in a system for accomplishing a given task such that all means must fail before causing a system failure. The reliability model is being studied here. The probabilities of component failure depend on the relative positions of the particular components along the hierarchy.

It is assumed that the n-components are arranged in the hierarchical order as If 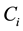is the active component during an attack, let and 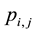are the probabilities that 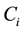survives, 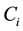fails, but survives etc., and be the probability that the components 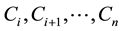fail in the same attack. Thus, we have, 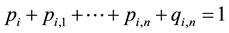for.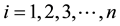

In the present, probability distribution of the number of attacks required for failure of a n-component hierarchical cascade system, as defined above, is investigated and the probability of the system surviving k attacks, sustained a loss of the first m components, is studied.

2. Notation and Explanations

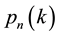: Probability that a n-component system fails in the kth attack.

: The corresponding probability distribution function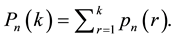

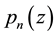: The corresponding probability generating function.

: The reliability of the n-component system surviving “k” attacks with a loss of “m” components.

: The probability of the n-component system surviving “k” attacks with a loss of “m” components.

: The event that survives “j” attacks.

: The event that fails at jth attacks.

: The event that the n-component system fails at the kth attack.

: The serial number of attack at which fails but does not fail.

: The event that fails at the βth attack and fails at the kth attack. When, is attacked but survives the attacks number. When, i.e., the component fails in the kth attack and also fails in the kth attack.

: The event that the system survives k attacks with a loss of the first m components.

: The transition probability matrix for a n-component system. This is a (n + 1)th order matrix. It should be noted that the (i + 1)th row stands for the initial state,. Similarly, for the columns.

: The element of. Thus,. The last row of this order matrix

consists of zeros except for unity at the column.

:

: Probability that fail and survives during an attack; is the first component facing this attack, components having failed during earlier attacks, if any.

: The probability that fail at an attack when is the first component facing this attack; components having failed during earlier attacks, if any.

: Serial number of attack at which fails.

Obviously,

Let a system consist of three components. The system with the hierarchical ordering will have the transition probability matrix.

3. Reliability Evaluation

Reliability of a System for k Attacks

Here consider the probability that the system survives “k” attacks with a loss of the first “m” components. Let is the reliability of the n-component system for “k” attacks with a loss of “m” components.

The Two Component System:

For m = 0, we get

For m = 1, we have the corresponding event

The corresponding probability

here means the event that ith component system fails at 2^nd attack.

It is obvious that when m = 2

The Three Component System:

When m = 0, we get

When m = 1, we have the corresponding event

Hence

here means the event that ith component system fails at the 2^nd attack.

When m = 2, the corresponding event

Hence

It is obvious that

The Four Component System:

When m = 0, we get

Similarly, for m = 1

For m = 2

For m = 3

For m = 4

The Five Component System:

For m = 0, we get

For m = 1, the corresponding probability

For m = 2,

For m = 3,

For m = 4,

For m = 5,

The Six Component System:

For m = 0, we get

For m = 1, the corresponding probability

For m = 2,

For m = 3,

For m = 4,

For m = 5,

For m = 6,

The general equation for probability of n-component system fails in the kth attack

The general equation for reliability of n-component system for kth attack

4. Example

Let us consider a transition probability matrix of order 7 for 6-component system

The first element in the ith column matrix represents the probability of failure of the system at the end of ith attack i.e.,.

Let us find the reliability of above system in 2 number of attacks

5. Conclusion

The present work deals with the cascade reliability model represented as Markovian model. Reliability of stress strength model is derived with Markovian Approach. In this paper, the reliability of n-cascade system for k attacks with loss of m components has been derived for n > 4 and the general formula for reliability of n cascade system for k number of attacks has been derived. Using above general equation reliability has been calculated numerically for 6-cascade system for 2-number of attacks.

NOTES

^*Corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Kapur, K.C. and Lamberson, L.R. (1977) Reliability in Engineering Design. John Wiley and Sons, Inc., New York.
[2]	Shoomans, M.L. (1968) Probabilistic Reliability an Engineering Approach. McGraw-Hill, New York.
[3]	Schatz, R., Shooman, M. and Shaw, L. (1974) Applications of Time-Dependent Stress-Strength Models of Non-Electrical and Electrical Systems. Proceedings of Reliability and Maintainability Symposium, January 1974, 540-547.
[4]	Narahari Pandit, S.N. and Sriwastav, G.L. (1975) Studies in Cascade Reliability—I. IEEE Transactions on Reliability, R-24, 53-57. http://dx.doi.org/10.1109/TR.1975.5215330
[5]	Tadjett, W.J. (1978) Base Estimation of Reliability for Mixture of Life Distribution. SIAM Journal of Applied Mathematics, 34, 692-703. http://dx.doi.org/10.1137/0134058
[6]	Raghavachar, A.C.N. and Pattabhi Ramacharyulu, N.C. (1983) Survival Function under Stress Attenuation in Cascade Reliability. OPSEARCH, 20, 190-207.
[7]	Raghavachar, A.C.N., Kesava Rao, B. and Narahari Pandit, S.N. (1987) The Reliability of a Cascade System with Normal Stress and Strength Distribution. ASR, 2, 49-54.
[8]	Sinha, S.K. (1986) Reliability and Life Testing. Weiley Eastren, New Delhi.
[9]	Uma Maheswari, T.S. (1993) Reliability of Cascade System with Normal Stress and Exponential Strength. Micro Electronics Reliability, 33, 927-936. http://dx.doi.org/10.1016/0026-2714(93)90289-b
[10]	Uma Maheswari, T.S. (1993) Reliability Comparison of an n-Cascade System with the Addition of an n-Strength System. Micro Electronics Reliability, 33, 477-479. http://dx.doi.org/10.1016/0026-2714(93)90313-N
[11]	Uma Maheswari, T.S. (1994) Reliability of Single Stress under n-Strengths of Life Distribution. Micro Electronics Reliability, 34, 569-572. http://dx.doi.org/10.1016/0026-2714(94)90097-3
[12]	Rekha, A. and Chenchu Raju, V.C. (1999) Cascade System Reliability with Rayleigh Distribution. Botswana Journal of Technology, 8, 14-19.
[13]	Maya, T.N. (2007) On a Finite Mixture of Pareto and Beta Distributions. Ph.D. Thesis Submitted to Cochin University of Science and Technology, Kerala.