Spherical Casimir Effect for a Massive Scalar Field on the Three Dimensional Ball

Andrea Erdas

Department of Physics, Loyola University Maryland, Baltimore, USA.

DOI: 10.4236/jmp.2015.68115                

Abstract

The zeta function regularization technique is used to study the Casimir effect for a scalar field of mass m satisfying Dirichlet boundary conditions on a spherical surface of radius a. In the case of large scalar mass, , simple analytic expressions are obtained for the zeta function and Casimir energy of the scalar field when it is confined inside the spherical surface, and when it is confined outside the spherical surface. In both cases the Casimir energy is exact up to order and contains the expected divergencies, which can be eliminated using the well established renormalization procedure for the spherical Casimir effect. The case of a scalar field present in both the interior and exterior region is also examined and, for , the zeta function, the Casimir energy, and the Casimir force are obtained. The obtained Casimir energy and force are exact up to order and respectively. In this scenario both energy and force are finite and do not need to be renormalized, and the force is found to produce an outward pressure on the spherical surface.

Keywords

Casimir Effect, Spherical, Dirichlet Boundary Conditions

1. Introduction

The electromagnetic Casimir effect was first predicted theoretically by H. G. B. Casimir [1] in 1948, when he showed that an attractive force exists between two electrically neutral, parallel conducting plates in vacuum. Boyer predicted the repulsive Casimir force some time later, when he discovered that a perfectly conducting, neutral spherical surface in vacuum modifies the vacuum energy of the electromagnetic field in such a way that the spherical surface is subject to an outward pressure [2] . Experimental confirmation of the Casimir effect came more than fifty years ago by Sparnaay [3] , and many improved experimental observations have been reported throughout the years [4] [5] .

Since their discovery, Casimir forces have been found to have many applications from nanotechnology to string theory, and a large effort has gone into studying the generalization of the Casimir effect to quantum fields other than the electromagnetic field: fermions were first considered by Johnson [6] then investigated by many others, and bosons and other scalar fields have also been investigated extensively [4] .

It is well known that Casimir forces are very sensitive to the boundary conditions of the quantum fields at the plates. In the case of scalar fields, Dirichlet and Neuman boundary conditions are most commonly used, in the case of fermion fields or other fields with spin [7] , bag boundary conditions are used. In this manuscript I investigate a scalar field that obeys Dirichlet boundary conditions on a spherical surface of radius a. While this paper investigates scalar fields within the context of a spherical geometry, the techniques that will be used in this paper can be extended to the case of other types of fields, such as fermions satisfying bag boundary conditions on the sphere. In the case of the parallel plates geometry, this extension to fermions was done in Ref. [8] . Another extension or application of this work could be within the context of the recent tests for the gravitational behavior of anti-matter, or antigravity experiments [9] . This paper could help understanding the phenomenon of quantum reflection of antimatter from spherical surfaces. This effect is relevant for the plate geometry to experi- ments such as GBAR where ultracold antihydrogen atoms are detected by annihilation on a plate ( [9] and re- ferences within).

Massive or massless scalar fields appear in many areas of physics from the Higgs field in the Standard Model, to the dilaton field that breaks the conformal symmetry in string theory, to the Ginzburg-Landau scalar field in superconductivity, etc.

The Casimir effect due to a scalar field has been studied extensively in the parallel plate and spherical geometry. Different regularization techniques have been used to remove the singularities of the Casimir energy such as, for example, the zeta function technique and the Casimir piston technique. While in the context of this work I will use the zeta function technique, the Casimir piston technique [10] - [12] is quite intriguing, being physically more direct in the case of the parallel plates geometry and, in the future, the Casimir spherical piston technique should be investigated.

The spherical Casimir effect for massless [13] [14] or massive [15] - [18] scalar fields in 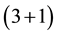or dimensions has been studied in vacuum and at finite temperature [19] [20] using the Green’s function method [13] [17] , the zeta function technique [14] - [16] [18] and the heat kernel expansion [21] - [23] to calculate the Casimir energy. These authors however, are only able to obtain the Casimir energy for large scalar mass as an infinite sum of hypergeometric functions. In this manuscript I use the zeta function technique to study the spherical Casimir effect for a scalar field of mass m and, without using the heat kernel expansion, obtain simple analytic forms for the zeta function and Casimir energy when the scalar field is confined inside or outside the spherical surface, in the case of large scalar mass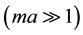. In both cases the Casimir energy is found to be divergent, as expected [15] [16] . I also obtain simple expressions for the large mass Casimir energy and force on the spherical surface in the case of a scalar field present both inside and outside the spherical surface. The energy and force obtained for this scenario are finite and differ from results obtained previously by authors that used the heat kernel expansion.

In Section 2, I describe the model and, for the case of a scalar field confined inside the spherical surface, obtain the zeta function 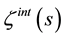using the Debye uniform asymptotic expansion of the modified Bessel functions. In Section 3, I find a simple expression for 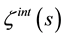in the large mass limit. In Section 4, I use the large mass limit of 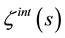to calculate the Casimir energy for a scalar field confined inside the spherical surface, in the case of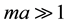. I also obtain, using 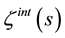from Section 3, the large mass limit of the zeta function and Casimir energy in the case of a scalar field confined outside the spherical surface. Finally I study the case of a scalar field present both inside and outside the spherical surface, and find very simple analytic expressions for the Casimir energy and force on the spherical shell, when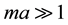. A summary and discussion of my results are presented in Section 5.

2. Zeta Function inside a Spherical Surface

In 3-dimensional space the equation of motion of a scalar field, 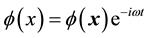, is the Klein-Gordon equation

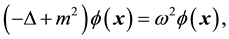
where m is the scalar field mass. Using spherical coordinates, this equation becomes

(1)

where is the angular momentum operator. After a separation of variables

the radial part of Equation (1) is found to be

(2)

A complete set of solutions of Equation (2), finite at the origin, is

where are Bessel functions of the first kind and. Once we impose Dirichlet boundary conditions on a spherical surface of radius a

we find

where is the n-th zero of and. The energy eigenvalues are found immediately

and, when the scalar field is confined inside the spherical surface, the zeta function is given by

(3)

where is the degeneracy of the eigenmodes of angular momentum l.

Since has simple poles at, I can write Equation (3) in the form of a contour inte- gral [21] [22]

where the closed contour runs counterclockwise, contains the whole positive k-axis and, with it, all of the

for and. Next I rotate the integration contour to the imaginary axis and obtain

(4)

where, is a modified Bessel function of the first kind, and the added factor inside the

logarithm does not change the result, since no additional pole is enclosed. A simple change of the integration variable allows me to rewrite Equation (4) as

(5)

and to exploit the Debye uniform asymptotic expansion of the modified Bessel functions [15]

(6)

where

and is defined recursively by

I use Equation (6) and find

(7)

where the are defined through

and are polynomials of degree 3i

while the coefficients can be easily calculated with a simple computer program. It is clear that, as N grows, the right side of Equation (7) becomes a more accurate approximation of the left side of (7). Using Equation (7), I write the following approximate expression of the zeta function

(8)

with

(9)

(10)

and, for

(11)

Equation (8) displays the same feature as Equation (7): as N grows the sum on the right side becomes a more accurate approximation of the zeta function. Notice that the coefficients of Equations (9)-(11) are defined in the same way as in [15] . Notice also that the authors of Ref. [15] use only the first five of the, ending the sum at, and therefore need to add a term, , that can only be evaluated numerically with considerable numerical challenges, since is defined as the difference of integrals whose values are nearly identical and many orders of magnitude larger than their difference. The alternative approach presented in this work ends the sum in Equation (8) at, with N high enough that one does not need to add a numerical term to Equation (8).

3. Zeta Function in the Large Mass Limit

In this section I evaluate the of Equation (8) in the limit, using a simpler and more direct method than the heat kernel expansion. At this stage, since the lower limit of integration in the three integrals (9 - 11) is very large, I use a large z asymptotic expansion of their integrands. When, I can write

and therefore, in the large mass limit, I find

(12)

Similarly

when, and thus and become

(13)

(14)

After I change the integration variable from z to in the integrals of Equations (12)-(14), use

and integrate over the new variable y, I obtain

and, for

The integrals over are done easily, and I find

(15)

(16)

and, for

(17)

where

is the Hurwitz zeta function.

4. Casimir Energy and Force in the Large Mass Limit

The Casimir energy for a massive scalar field confined inside a spherical surface of radius a, is given by

where is given by Equation (8), and therefore I obtain the large mass limit of using Equations (15)-(17) for the large mass limits of the. I find

(18)

for, where is the Riemann zeta function of number theory and is the Euler

Mascheroni constant, and where I neglected all terms of order with, since. Similarly, I find

(19)

(20)

(21)

where I used, , and neglected all terms of order with. The expansions of the

derived in Equations (18)-(21) are different from those obtained by other authors [15] . Notice that, since

the contribution of is of order, I do not need to consider any with, and there- fore the exact large mass limit of to order is

(22)

where the are given by Equations (18)-(21). Notice also that, as, the expected diver- gencies [15] only appear in and, due to the factors of and present inside Equ- ations (15) and (17). All the other are free of divergencies as, since is finite when

and. This result for the Casimir energy is different from the one obtained using the heat kernel method [15] [23] .

The appearance of divergencies in the calculation of requires renormalization of the Casimir energy, and I will use the same renormalization procedure presented first in Ref. [15] . The physical system examined in this paper consists of a classical and a quantum part. The classical part is a spherical surface of radius a with energy

where is the volume, p is the pressure, is the surface, the surface tension and F, k,

and h do not have names. The quantum part of the system under consideration is a scalar field satisfying Dirichlet boundary condition on the spherical surface. The ground state energy of this scalar field, , is divergent and will be renormalized following the scheme described in [15] : divergent contributions to will be subtracted by means of a renormalization of the corresponding parameters in. This renormalization is achieved by shifting the parameters in by an amount which cancels the contributions of the two co-

efficients and, that diverge as. The two parameters in that need to be shifted

are F and h, since and.

If the scalar field is confined outside the spherical surface, the zeta function is [15]

(23)

and can be used to calculate, the Casimir energy for the exterior region. The large mass limit of,

exact to order, is

(24)

with the given by Equations (18)-(21). Since and contain divergent

terms as, the Casimir energy for the exterior region is also divergent, as expected, but different from the one obtained in Refs. [15] [23] . The renormalization of the divergent Casimir energy can be carried out using the same procedure outlined above for [15] .

Finally, I discuss the situation where the scalar field is present in both the interior and exterior regions. In this case the Casimir energy is

and, using Equations (22) and (24), I find a finite value for the large mass limit of E

(25)

again different from what appears in the literature [5] . Notice that, as, the Casimir energy. The Casimir force F on the spherical surface of radius a is given by

and I find a repulsive force

(26)

indicating an outward pressure on the spherical surface, that vanishes as. The large mass limit Casimir

energy E and force F that I find in Equations (25) and (26), are exact to order and respectively.

5. Discussion and Conclusions

In this manuscript I used the zeta function regularization technique to study the spherical Casimir effect of a massive scalar field in dimensions. I analyzed three scenarios: a scalar field confined inside a spherical surface, a scalar field confined outside the spherical surface, and a scalar field present inside and outside the spherical surface at the same time. In all cases Dirichlet boundary conditions were imposed on the sphere of radius a. I obtained two expressions of the zeta function in the large mass limit, one valid inside the sphere and

one valid outside, which are exact to order, and used them to obtain the large mass limit of the Casimir energy inside (22) and outside the sphere (24), exact to order. These Casimir energies contain diver-

gencies, as I expected, and can be renormalized following the renormalization procedure described in Ref. [15] , but disagree with the values calculated in previous papers that use the heat kernel expansion [5] [15] [23] .

Finally, I studied the case of a scalar field present both inside and outside the spherical surface, and obtained the large mass limit of the Casimir energy (25) and force (26) in this case. Both quantities are finite and thus do

not need to be renormalized, and are exact to order and respectively. Also these results do not agree with previously published results [5] [15] [23] .

For a scalar field with mass, such as the Higgs, I find that any spherical surface of radius, with, abundantly satisfies the large mass condition, since. In this scenario, I find that the Casimir force on the spherical surface is, where is obtained by using and in Equation (26).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Casimir, H.B.G. (1948) Kon. Ned. Akad. Wetensch. Proc., 51, 793.
[2]	Boyer, T.H. (1968) Physical Review, 174, 1764. http://dx.doi.org/10.1103/PhysRev.174.1764
[3]	Sparnaay, M.J. (1958) Physica, 24, 751-764. http://dx.doi.org/10.1016/S0031-8914(58)80090-7
[4]	Bordag, M., Mohideen, U. and Mostepanenko, V.M. (2001) Physics Reports, 353, 1-205. http://dx.doi.org/10.1016/S0370-1573(01)00015-1
[5]	Bordag, M., Klimchitskaya, G.L., Mohideen, U. and Mostepanenko, V.M. (2009) Advances in the Casimir Effect. International Series of Monographs on Physics Vol. 145, Oxford University, New York, 1. http://dx.doi.org/10.1093/acprof:oso/9780199238743.003.0001
[6]	Johnson, K. (1975) Acta Phys. Pol. B, 6, 865.
[7]	Ambjorn, J. and Wolfram, S. (1983) Annals of Physics, 147, 1-32. http://dx.doi.org/10.1016/0003-4916(83)90065-9
[8]	Oikonomou, V.K. and Tracas, N.D. (2010) International Journal of Modern Physics A, 25, 5935. http://dx.doi.org/10.1142/S0217751X10051189
[9]	Dufour, G., Cassidy, D.B., Crivelli, P., Debu, P., Lambrecht, A., Nesvizhevsky, V.V., Reynaud, S., Voronin, A.Y. and Wall, T.E. (2015) Advances in High Energy Physics, 2015, Article ID: 379642. http://dx.doi.org/10.1155/2015/379642
[10]	Fulling, S.A., Kaplan, L., Kirsten, K., Liu, Z.H. and Milton, K.A. (2009) Journal of Physics A: Mathematical and Theoretical, 42, Article ID: 155402. http://dx.doi.org/10.1088/1751-8113/42/15/155402
[11]	Elizalde, E., Odintsov, S.D. and Saharian, A.A. (2009) Physical Review D, 79, Article ID: 065023. http://dx.doi.org/10.1103/PhysRevD.79.065023
[12]	Oikonomou, V.K. (2009) Modern Physics Letters A, 24, 2405-2423. http://dx.doi.org/10.1142/S0217732309031703
[13]	Bender, C.M. and Milton, K.A. (1994) Physical Review D, 50, 6547-6555. http://dx.doi.org/10.1103/PhysRevD.50.6547
[14]	Cognola, G., Elizalde, E. and Kirsten, K. (2001) Journal of Physics A, 34, 7311-7327. http://dx.doi.org/10.1088/0305-4470/34/36/311
[15]	Bordag, M., Elizalde, E., Kirsten, K. and Leseduarte, S. (1997) Physical Review D, 56, 4896-4904. http://dx.doi.org/10.1103/PhysRevD.56.4896
[16]	Kirsten, K. (2000) http://arxiv.org/abs/hep-th/0005133.
[17]	Saharian, A.A. (2001) Physical Review D, 63, Article ID: 125007. http://dx.doi.org/10.1103/PhysRevD.63.125007
[18]	de Mello, E.R.B., Bezerra, V.B. and Khusnutdinov, N.R. (2001) Journal of Mathematical Physics, 42, 562. http://dx.doi.org/10.1063/1.1333699
[19]	Balian, R. and Duplantier, B. (1978) Annals of Physics, 112, 165-208. http://dx.doi.org/10.1016/0003-4916(78)90083-0
[20]	Teo, L.P. (2013) Journal of Mathematical Physics, 54, Article ID: 103505. http://dx.doi.org/10.1063/1.4824466
[21]	Bordag, M. and Kirsten, K. (1995) http://arxiv.org/abs/hep-th/9501064.
[22]	Bordag, M., Elizalde, E. and Kirsten, K. (1996) Journal of Mathematical Physics, 37, 895. http://dx.doi.org/10.1063/1.531418
[23]	Bordag, M. and Kirsten, K. (1996) Physical Review D, 53, 5753-5760. http://dx.doi.org/10.1103/PhysRevD.53.5753