Molecular Structure, Vibrational Assignments and Non-Linear Optical Properties of 4,4’ Dimethylaminocyanobiphenyl (DMACB) by DFT and ab Initio HF Calculations ()
1. Introduction
Non linear optical (NLO) phenomena are of significance because they form the basis of the optical processing and data storage. Therefore, they are important in the development of the future generations of communication systems and computers, and much effort has been devoted to increasing the useful non linearity of optical materials [1] [2] . Depending on the particular application, the use of organic materials may offer majored vantages over conventional inorganic crystals [3] [4] . In the past years, considerable efforts focused on the development of organic materials with large molecular hyperpolarizabilities, improved optical transparency, etc. [5] [6] . For a material having useful and highly efficient nonlinear optical properties, the constituting molecules need first to exhibit large molecular hyperpolarizabilities, which are generally characterized by a highly extended π-conju- gated chain with electron donor-acceptor pair at the ends (D-π-A). The existences of strong intermolecular charge transfer excitations in a noncentrosymmetric molecular environment are key to the non linear optical activity. The first criterion can be satisfied by considering a polarizable molecular system (e.g. π conjugated pathway) having an uneven or asymmetric charge distribution. The simplest way to achieve this is to have a donor (D)―acceptor (A) system with a bridge (D-π-A) which can help the electronic communication between the donor and the acceptor. In this study, the geometrical parameters, fundamental frequencies of the title compound in the ground state have been calculated by using the HF and DFT (B3LYP, B3PW91) methods with 6-31G(d, p) basis set. The non-linear optical properties are also addressed theoretically. The electric dipole moment μ, the isotropic polarizability α and the first hyperpolarizability β of the title compound are calculated.
DMACB is a derivative of a “Push Pull” molecule crystallises in a non centrosymetric group Cc, with four molecules in the unit cell. This molecule consists of the set of two benzene rings which are fixed to oppose an electron donor (dimethylamino group), characterized by Hammett coefficient (−1.70) and an electron acceptor (cyano group) (electron-withdrawing by a Hammett’s coefficient equal to 0.66). The positive value of Hammett coefficient reflects an electro-attractor acceptor effect. This compound is a very suitable material for the non-linear optics. Our objective is to design a range of molecular systems, which show NLO activity. The approach is based on the concept of charge transfer (CT) between donor and acceptor through a biphenyl. The designing of systems with high CT is key to this part, as intra molecular CT between the donor and acceptor will lead to a very large value for β.
2. Computation Methods
The HF theory applies the self-consistent field level and is thus very appropriate for such calculations. On the other hand, DFT was applied using the B3LYP which is the keyword for the hybrid functional [7] , which is a linear combination of the gradient functional proposed by Becke [8] and Lee, Yang and Parr [9] , together with the Hartree Fock local exchange function [10] . DFT was also applied using the B3PW91 functional, which implies its use of a three-parameter scheme, as well as, the generalized gradient approximation exchange and correlation functional B [7] and PW91 [11] . PW91 uses a different expression for the local density approximation and contains no empirical parameters. Calculations were performed using the Gaussian 03 [12] . The HF and DFT methods with 6-31G(d, p) basis set calculations were made first to optimize the structures. The vibrational frequencies and non-linear optical properties were calculated by means of the HF and DFT methods at the corresponding optimized geometries. All the calculations converged to an optimized geometry which corresponds to a true energy minimum as revealed by the lack of imaginary values in the calculate vibration frequencies. Vibration frequencies are calculated using HF/6-31G(d, p), B3LYP/6-31G(d, p), B3PW91/6-31G(d, p) and then scaled by 0.89, 0.95, and 1 respectively. In this work, to improve the agreement with experiment, the B3LYP/ 6-31G(d, p) harmonic frequencies were scalled by a factor of 0.95. The NLO response calculation was performed on the optimized geometry using the same level of theory. The first static hyperpolarizability β is a third rank tensor that can be described by a 3 × 3 × 3 matrix. The 27 components of the 3D matrix can be reduced to 10 components due to the Kleinman symmetry [13] (βxyy = βyxy = βyyx, βyyz = βyzy = βzyy ..., likewise other permutations also take same value). It can be given in the lower tetrahedral format. The output from Gaussian 03 provides 10 components of this matrix as βxxx, βxxy, βxyy, βyyy, βxxz, βxyz, βyyz, βxzz, βyzz, βzzz, respectively. Many types of hyperpolarizabilities have been discussed in the literature [14] . When reporting a single value of β, one of the common formats is to simply treat the three independent values for β as a quasi-Pythagorean problem and solve for the average β by Equation (1):
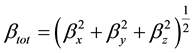 (1)
(1)
The complete equation for calculating the magnitude of the total first static hyperpolarizability from Gaussian 03 output is given as Equation (2):
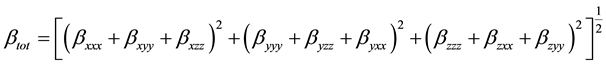 (2)
(2)
3. Results and Discussion
3.1. Molecular Parameters
The atomic numbering scheme and the theoretical geometric structure for the title compound crystal [15] are shown in Figure 1 and Figure 2. The crystal structure of the title compound is monoclinic with space group Cc. The crystal structure parameters of the title compound are a = 9.503(2) Å, b = 16.429(6) Å, c = 8.954(4) Å, β = 122.04(3) Å, The volume of the unit cell is V= 1185.0(8) Å3 [15] . The optimized parameters (bond lengths and angles of the title compound have been obtained at the HF and B3LYP methods with 6-31G (d, p) basis set.
![]() (a)
(a)![]() (b)
(b)
Figure 1. The DMACB molecule projected on a plane parallel. (a) and perpendicular; (b) to the cyanobenzene ring [15] .
![]()
![]()
Figure 2. B3LYP/6-31G** optimized structure of 4, 4’dimethylaminocyanobiphenyl.
These results are listed in Table 1 and Table 2 and compared with the experimental data of the title compound. The geometries predicted by the HF calculations are a little better than the DFT computations. For C(13)≡N(1) distance, the good agreement between experiment and calculation was noticed. In real crystal, this distance is equal to 1.14 Å and in DFT approach is a little bigger (1.16 Å). The all calculated C-H distances are very similar and equal (1.085 Å). In experimental results the differences are observed. These lengths are included in the range of 0.90 - 1.05 Å. from the theoretical values; it is noteworthy that most of the optimized angles have slightly larger values than the corresponding experimental ones, due to the fact that theoretical calculations imply isolated molecules in gaseous phase state while experimental results refer to molecules in the solid state.
3.2. Assignments of the Vibration Modes
The vibrational spectral studies also provide information about the charge transfer interaction between the donor
![]()
Table 1. Optimized geometry of DMACB calculated at the Hartree Fock, DFT levels of theory using the 6-31G(d, p) basis set (bond length ) ,with estimated standard deviations in parentheses.
![]()
Table 2. Optimized geometry of DMACB calculated at the Hartree Fock, DFT levels of theory using the 6-31G(d, p) basis set (bond angle) with estimated standard deviations in parentheses.
and acceptor groups through π-electron movement. This π-electron cloud makes the molecule highly polarized and the intermolecular charge transfer interaction is highly responsible for the NLO properties of the title compound. Based on optimized geometries, the vibrational frequencies have been performed by the same methods and basis set. The vibrational bands assignments have been made by using Gauss-View molecular visualization program [16] . Theoretical results of the title compound are shown in Table 3. Nitrogen compounds featuring triple or cumulated double bonds, such as cyanides or nitriles (−C≡N) and cyanates −O−(C≡N), all provide a unique spectrum, typically with a single, normally intense absorption at 2280 - 2200 cm−1 (for cyano compounds) and 2285 - 1990 cm−1 (for cyanates, isocyanates and thiocyanates) [17] [18] . The calculated value for the stretching mode υ C≡N with DFT-B3LYP is 2342 cm−1, Medium to weak absorption bands for the unconjugated C-N linkage in primary, secondary and tertiary aliphatic amines appear in the region of 1250 - 1020 cm−1 [19] . The vibrations responsible for these bands involve C-N stretching couples with the stretching of adjacent bonds in the molecules. The position of absorption in this region depends on the class of amine and the pattern of substitution on the α carbon. Aromatic amines display strong C-N stretching absorption in 1342 - 1266 cm−1 region [19] [20] . The absorption appears at higher frequencies than the corresponding absorption of aliphatic amines because the force constant of the C−N bond is increased by resonance with the ring. Louran et al. [21] reported a value at 1220 cm−1 for υ CN for polyaniline. For the title compound the υ CN mode is observed at 1203 cm−1 theoretically. For benzenes υ CH stretching mode are seen in the range 3230 - 3188 cm−1, υ CC stretching mode are seen in the range 1676 - 1447 cm−1 and δ CH vibrations are seen in the range 1230 - 1280 cm−1 and 1170 - 1000 cm−1 [21] .We have observed theoretical values at 1480 to 1394 and 1312 to 1145 cm−1. The out-of-plane CH deformation bands ω CH are expected in the range 740 - 990 cm−1 [21] . As seen from Table 3, the DFT-B3LYP calculation give wave numbers at 863,829 cm−1. The theoretical calculation Bands corresponding to CH3 asymmetric and symmetric bending vibrations are observed at 3150 cm−1 to 2995 cm−1 respectively.
![]()
Table 3. Calculated vibrational spectra of the title compound (C15H14N2).
ν stretching modes (νs symmetric, ν as antisymmetric). δ in plane valence angle bending. τ, ω, β: torsion out of plan, wagging and rocking deformations respectively.
(a) ![]() (b)
(b) ![]() (c)
(c) ![]()
Table 4. (a) The electric dipole moment μ (D); (b) The average polarizability αtot (×10−24 esu); (c) The first hyperpolarizability βtot (×10−31 esu).
3.3. Hyperpolarizability Calculation
As mentioned above, this study is extended to the determination of the electric dipole moment μ, the isotropic polarizability α and the first hyperpolarizability β of the title compound. Since the values of the polarizability α and the first hyperpolarizability β of Gaussian 03 output are reported in atomic units (a.u.), the calculated values have been converted into electrostatic units (esu) (α: 1 a.u. = 0.1482 × 10−24 esu; β: 1 a .u. = 8.6393 × 10−33 esu). Table 4 listed the HF/6-31G(d, p), B3LYP/6-31G(d, P) ,B3LYP/6-31G/(d, p) results of the electronic dipole moment µ, polarizability α and the first hyperpolarizability β for 4,4’ dimethylaminocyanobiphenyl. The highest value of dipole moment is calculated by B3PW91 is equal to 8.66 D (Debye). The highest value of dipole moment is observed for component µz. In this direction, this value is equal to 0.12 D. For direction x and y, these values are equal to −8.66 D and 0.03 D respectively. The dipole moment by HF and B3LYP values of the title compound are 6.60 D, 8.50 D respectively. The calculated polarizability α by HF, B3LYP and B3PW91 are equal to 24.39 × 10−24 esu, 28.87 × 10−24 esu, and 28.88 × 10−24 respectively. As we can see in Table 4, the calculated polarizability αij have non zero values and was dominated by the diagonal components. The first hyperpolarizability values βtot of the title compound are equal to 99.77 × 10−31 esu, 489.88 × 10−31 esu and 499.87 × 10−31 esu calculated by HF, B3LYP and B3PW91 respectively. The hyperpolarizability β dominated by the longitudinal component of βzzz. Domination of particular components indicates on a substantial delocalization of charges in these directions. Consequently, we can finally infer from the above discussion of the contents of Table 4 that the introduction of electron correlation in the method applied for the analysis of the hyperpolarizability, such as the DFT method, will probably predict more reasonable values as opposed to those converged upon use of the HF method, which yields very poor results.
4. Conclusion
In this work we have calculated the geometric parameters, the vibrational frequencies and the non linear optical properties of 4,4’ dimethylaminocyanobiphenyl by using HF and DFT (B3LYP and B3PW91) methods. The optimized geometric bond lengths and bond angles obtained by using HF and DFT (B3LYP and B3PW91) show a good agreement with the experimental data. The comparison between the calculated vibrational frequencies by using HF and DFT methods indicates that B3PW91 is superior to the scaled HF and B3LYP approach for molecular vibrational problems. Nonlinear optical NLO behavior of the examined compound is investigated by the determination of the electric dipole moment, the polarizability and the hyperpolarizability by using the HF and DFT methods.