A Strong Law of Large Numbers for Set-Valued Random Variables in Gα Space ()
1. Introduction
We all know that the limit theories are important in probability and statistics. For single-valued case, many beautiful results for limit theory have been obtained. In [1], there are many results of laws of large numbers at different kinds of conditions and different kinds of spaces. With the development of set-valued random theory, the theory of set-valued random variables and their applications have become one of new and active branches in probability theory. And the theory of set-valued random variables has been developed quite extensively (cf. [2]- [7] etc.). In [1], Artstein and Vitale used an embedding theorem to prove a strong law of large numbers for independent and identically distributed set-valued random variables whose basic space is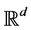 , and Hiai extended it to separable Banach space
, and Hiai extended it to separable Banach space 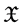 in [8]. Taylor and Inoue proved SLLN's for only independent case in Banach space in [7]. Many other authors such as Giné, Hahn and Zinn [9], Puri and Ralescu [10] discussed SLLN's under different settings for set-valued random variables where the underlying space is a separable Banach space.
in [8]. Taylor and Inoue proved SLLN's for only independent case in Banach space in [7]. Many other authors such as Giné, Hahn and Zinn [9], Puri and Ralescu [10] discussed SLLN's under different settings for set-valued random variables where the underlying space is a separable Banach space.
In this paper, what we concerned is the SLLN of set-valued independent random variables in 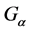 space. Here the geometric conditions are imposed on the Banach spaces to obtain SLLN for set-valued random varia- bles. The results are both the extension of the single-valued’s case and the extension of the set-valued’s case.
space. Here the geometric conditions are imposed on the Banach spaces to obtain SLLN for set-valued random varia- bles. The results are both the extension of the single-valued’s case and the extension of the set-valued’s case.
This paper is organized as follows. In Section 2, we shall briefly introduce some definitions and basic results of set-valued random variables. In Section 3, we shall prove a strong law of large numbers for set-valued inde- pendent random variables in 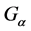 space.
space.
2. Preliminaries on Set-Valued Random Variables
Throughout this paper, we assume that 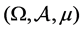 is a nonatomic complete probability space,
is a nonatomic complete probability space, 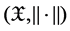 is a real separable Banach space,
is a real separable Banach space, 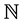 is the set of nature numbers,
is the set of nature numbers, 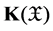 is the family of all nonempty closed subsets of
is the family of all nonempty closed subsets of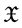 , and
, and 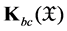 is the family of all nonempty bounded closed convex subsets of
is the family of all nonempty bounded closed convex subsets of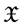 .
.
Let 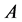 and
and 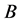 be two nonempty subsets of
be two nonempty subsets of 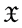 and let
and let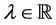 , the set of all real numbers. We define addi- tion and scalar multiplication as
, the set of all real numbers. We define addi- tion and scalar multiplication as
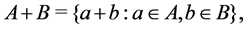
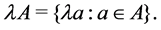
The Hausdorff metric on ![]() is defined by
is defined by
![]()
for![]() . For an
. For an ![]() in
in![]() , let
, let![]() . The metric space
. The metric space ![]() is complete , and
is complete , and ![]() is a closed subset of
is a closed subset of ![]() (cf. [6], Theorems 1.1.2 and 1.1.3). For more general hyper-
(cf. [6], Theorems 1.1.2 and 1.1.3). For more general hyper-
spaces, more topological properties of hyperspaces, readers may refer to a good book [11].
For each![]() , define the support function by
, define the support function by
![]()
where ![]() is the dual space of
is the dual space of![]() .
.
Let ![]() denote the unit sphere of
denote the unit sphere of![]() ,
, ![]() the all continuous functions of
the all continuous functions of![]() , and the norm is defined as
, and the norm is defined as ![]()
The following is the equivalent definition of Hausdorff metric.
For each![]() ,
,
![]()
A set-valued mapping ![]() is called a set-valued random variable (or a random set, or a multifunction) if, for each open subset
is called a set-valued random variable (or a random set, or a multifunction) if, for each open subset ![]() of
of![]() ,
,![]() .
.
For each set-valued random variable![]() , the expectation of
, the expectation of![]() , denoted by
, denoted by![]() , is defined as
, is defined as
![]()
where ![]() is the usual Bochner integral in
is the usual Bochner integral in![]() , the family of integrable
, the family of integrable ![]() -valued random variables, and
-valued random variables, and![]() . This integral was first introduced by Aumann [3], called Aumann integral in literature.
. This integral was first introduced by Aumann [3], called Aumann integral in literature.
3. Main Results
In this section, we will give the limit theorems for independent set-valued random variables in ![]() space. The following definition and lemma are from [1], which will be used later.
space. The following definition and lemma are from [1], which will be used later.
Definition 3.1 A Banach space ![]() is said to satisfy the condition
is said to satisfy the condition ![]() for some
for some![]() , if there exists a mapping
, if there exists a mapping ![]() such that
such that
(i)![]() ;
;
(ii)![]() ;
;
(iii) ![]() for all
for all ![]() and some positive constant
and some positive constant![]() .
.
Note that Hilbert spaces are ![]() with constant
with constant ![]() and identity mapping
and identity mapping![]() .
.
Lemma 3.1 Let ![]() be a separable Banach space which is
be a separable Banach space which is ![]() for some
for some ![]() and let
and let ![]() be single-valued independent random elements in
be single-valued independent random elements in ![]() such that
such that ![]() and
and ![]() for each
for each ![]() then
then
![]()
where ![]() is the positive constant in (iii).
is the positive constant in (iii).
Theorem 3.1 Let ![]() be a separable Banach space which is
be a separable Banach space which is ![]() for some
for some![]() . Let
. Let ![]() be a sequence of independent set-valued random variables in
be a sequence of independent set-valued random variables in![]() , such that
, such that ![]() for each
for each![]() . If
. If
![]()
where ![]() for
for ![]() and
and ![]() for
for![]() , then
, then ![]() converges with probability 1 in the sense of
converges with probability 1 in the sense of![]() .
.
Proof. Define
![]()
Note that ![]() for each
for each ![]() and that both
and that both ![]() and
and ![]() are independent se- quences of set-valued random variables. Next, for each
are independent se- quences of set-valued random variables. Next, for each ![]() and
and ![]()
![]()
That means ![]() is a Cauchy sequence and hence
is a Cauchy sequence and hence
![]()
as![]() . Since convergence in the mean implied convergence in probability, Ito and Nisio’s result in [12] for independent random elements(rf. Section 4.5) provides that
. Since convergence in the mean implied convergence in probability, Ito and Nisio’s result in [12] for independent random elements(rf. Section 4.5) provides that
![]()
Then for![]() , by triangular inequality we have
, by triangular inequality we have
![]()
By the completeness of![]() , we can have
, we can have ![]() converges almost everywhere in the sense of
converges almost everywhere in the sense of![]() .
.
Since by equivalent definition of Hausdorff metric, we have
![]()
For any fixed![]() , there exists a sequence
, there exists a sequence![]() , such that
, such that
![]()
Then by dominated convergence theorem, Minkowski inequality and Lemma 3.1, we have
![]()
for each ![]() and
and![]() . Thus,
. Thus, ![]() is a Cauchy sequence, and hence converges. Hence, by the similar way as above to prove
is a Cauchy sequence, and hence converges. Hence, by the similar way as above to prove ![]() converges with probability one in the sense of
converges with probability one in the sense of![]() . We also can prove that
. We also can prove that
![]()
with probability one in the sense of![]() . The result was proved. W
. The result was proved. W
From theorem 3.1, we can easily obtain the following corollary.
Corollary 3.2 Let ![]() be a separable Banach space which is
be a separable Banach space which is ![]() for some
for some![]() . Let
. Let ![]() be a sequence of independent set-valued random variables in
be a sequence of independent set-valued random variables in ![]() such that
such that ![]() for each
for each![]() . If
. If
![]() are continuous and such that
are continuous and such that ![]() and
and ![]() are non-decreasing, then for each
are non-decreasing, then for each ![]() the convergence of
the convergence of
![]()
implies that
![]()
converges with probability one in the sense of![]() .
.
Proof. Let
![]()
If![]() , by the non-decreasing property of
, by the non-decreasing property of![]() , we have
, we have
![]()
That is
![]() (4.1)
(4.1)
If![]() , by the non-decreasing property of
, by the non-decreasing property of![]() , we have
, we have
![]()
That is
![]() (4.2)
(4.2)
Then as the similar proof of theorem 3.1, we can prove both ![]() and
and ![]() converges with probability one, and the result was obtained. W
converges with probability one, and the result was obtained. W
Acknowledgements
The research was supported by NSFC(11301015, 11401016, 11171010), BJNS (1132008).