Uniform Convergence and Dynamical Behavior of a Discrete Dynamical System ()
1. Introduction
Let 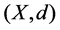 be a compact metric space and let
be a compact metric space and let 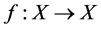 be a continuous map. Then the rule
be a continuous map. Then the rule 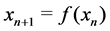 defines a discrete dynamical system. For an given initial condition
defines a discrete dynamical system. For an given initial condition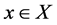 , the set
, the set 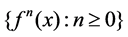 defines the orbit of the system.
defines the orbit of the system.
A point 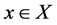 is called periodic if
is called periodic if 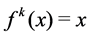 for some positive integer
for some positive integer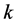 , where
, where 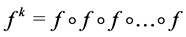 (
(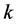 times). The least such
times). The least such 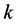 is called the period of the point
is called the period of the point . A map
. A map 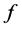 is called transitive if for any pair of non-empty open sets
is called transitive if for any pair of non-empty open sets ![]() in
in![]() , there exist a positive integer
, there exist a positive integer ![]() such that
such that![]() . A map
. A map ![]() is called weakly mixing if for any pairs of non-empty open sets
is called weakly mixing if for any pairs of non-empty open sets ![]() and
and ![]() in
in![]() , there exists
, there exists ![]()
such that ![]() for
for![]() . It is known that for any continuous self map
. It is known that for any continuous self map![]() , if
, if ![]() is weakly mixing and
is weakly mixing and ![]() are non-empty open sets, then there exists a
are non-empty open sets, then there exists a ![]() such that
such that ![]() for
for![]() . A map
. A map ![]() is called mixing or topologically mixing if for each pair of non-empty open sets
is called mixing or topologically mixing if for each pair of non-empty open sets ![]() in
in![]() , there exists a positive integer
, there exists a positive integer ![]() such that
such that ![]() for all
for all![]() .
.
A map ![]() is called sensitive if there exists a
is called sensitive if there exists a ![]() such that for each
such that for each![]() ,
, ![]() there exists
there exists ![]() and a positive integer
and a positive integer ![]() such that
such that ![]() and
and![]() . A map
. A map ![]() is called strongly sensitive if there exists a
is called strongly sensitive if there exists a ![]() such that for each
such that for each ![]() and each neighborhood
and each neighborhood ![]() of
of![]() , there exists a positive integer
, there exists a positive integer ![]() such that
such that ![]() for all
for all![]() . For Details refer [1]-[3].
. For Details refer [1]-[3].
For non-empty open subsets ![]() of
of![]() , Define,
, Define,
![]()
![]()
![]()
![]()
For any two continuous self maps ![]() on
on![]() , define
, define
![]() .
.
It can be seen that ![]() defines a metric on the space of all continuous functions.
defines a metric on the space of all continuous functions.
Let ![]() be sequence of continuous maps on
be sequence of continuous maps on![]() . The sequence is said to converge uniformly to a function
. The sequence is said to converge uniformly to a function ![]() if for each
if for each![]() ,
, ![]() such that
such that![]() .
.
In real systems, it is often observed that due to natural constraints, any modeling of a system yields a discrete or continuous system which approximates the behavior of the original system. Thus, it is interesting to see how the dynamics of approximations effect the dynamics of the original system. In this direction, we prove that many of the dynamical properties of the system cannot be concluded even with the strongest form of approximation. We prove that if a sequence of sensitive maps converges uniformly to a function![]() , the map
, the map ![]() need not be sensitive. Similar conclusions can be made for dynamical properties like transitivity and dense set of periodic points. We derive conditions under which uniform limit of weakly mixing/topologically mixing maps is weakly mixing/topologically mixing. In recent times, some of these questions have grabbed attention. In [4], authors claimed that uniform limit of a sequence of transitive maps is transitive. However, the claim proved to be false, was corrected in [5] [6] where authors proved that uniform convergence of transitive maps need not be transitive.
need not be sensitive. Similar conclusions can be made for dynamical properties like transitivity and dense set of periodic points. We derive conditions under which uniform limit of weakly mixing/topologically mixing maps is weakly mixing/topologically mixing. In recent times, some of these questions have grabbed attention. In [4], authors claimed that uniform limit of a sequence of transitive maps is transitive. However, the claim proved to be false, was corrected in [5] [6] where authors proved that uniform convergence of transitive maps need not be transitive.
In this paper we try to answer some of the above raised questions. We prove that many of the above mentioned properties are not preserved even under the strongest notion of convergence. In particular we prove that if the maps ![]() have positive topological entropy, the limit map need not have a positive topological entropy. We derive conditions under which properties like transitivity, dense periodic points and sensitive dependence on initial conditions are preserved.
have positive topological entropy, the limit map need not have a positive topological entropy. We derive conditions under which properties like transitivity, dense periodic points and sensitive dependence on initial conditions are preserved.
2. Main Results
We first give some examples to show that properties under consideration need not be preserved under uniform convergence.
Example 1: Let ![]() be a sequence of irrational numbers converging to 1. Let
be a sequence of irrational numbers converging to 1. Let ![]() defined as,
defined as,
![]()
It may be noted that as ![]() are irrationals, each
are irrationals, each ![]() is transitive but the limit is the identity map which is not transitive.
is transitive but the limit is the identity map which is not transitive.
If we take the sequence ![]() of rational numbers converging to an irrational number
of rational numbers converging to an irrational number![]() , then the sequence
, then the sequence ![]() is a sequence of maps with dense periodic; points but the limit function does not contain any periodic point.
is a sequence of maps with dense periodic; points but the limit function does not contain any periodic point.
Example 2: Let ![]() be the unit interval and
be the unit interval and ![]() be the unit circle. Then the product
be the unit circle. Then the product ![]() is a cylinder and the metric
is a cylinder and the metric ![]() gives the product topology on it.
gives the product topology on it.
For each![]() , define
, define ![]() as,
as,
![]()
Then for the map![]() , as any two points at different heights rotate with different velocities and move apart in finitely many iterates, for each
, as any two points at different heights rotate with different velocities and move apart in finitely many iterates, for each ![]() and any neighborhood
and any neighborhood ![]() of
of![]() , there are points in
, there are points in ![]() (at different height) which move apart in finitely many iterates and hence each
(at different height) which move apart in finitely many iterates and hence each ![]() is strongly sensitive. However, the limit of the sequence
is strongly sensitive. However, the limit of the sequence ![]() is the identity map which is not sensitive and hence sensitivity/strong sensitivity is not preserved under uniform convergence.
is the identity map which is not sensitive and hence sensitivity/strong sensitivity is not preserved under uniform convergence.
From the examples above, it is proved that the dynamical behavior of a sequence of dynamical systems need not be preserved even under the strongest form of convergence. We now give some necessary and sufficient conditions under which some of the dynamical properties of a sequence of dynamical systems ![]() are preserved in the limit map
are preserved in the limit map![]() .
.
Result 1: Let ![]() be a compact metric space and let
be a compact metric space and let ![]() be a sequence of self maps on
be a sequence of self maps on ![]() converging uniformly to
converging uniformly to![]() . Then,
. Then, ![]() is transitive if and only if for any pair of non-empty open sets in
is transitive if and only if for any pair of non-empty open sets in![]() ,
,
![]() .
.
Proof. Let ![]() be transitive and let
be transitive and let ![]() be two non-empty open sets in
be two non-empty open sets in![]() . As
. As ![]() is transitive, there exists
is transitive, there exists ![]() such that
such that![]() . Therefore, there exists
. Therefore, there exists ![]() such that
such that![]() . As
. As![]() , there exists
, there exists ![]() such that
such that ![]()
![]() . Thus,
. Thus,![]() . Consequently
. Consequently ![]() and proof of the forward part is complete.
and proof of the forward part is complete.
Conversely, let ![]() be two non-empty open sets in
be two non-empty open sets in![]() . Let
. Let ![]() and
and![]() . Choose
. Choose ![]() such that
such that ![]() and
and![]() . Let
. Let ![]() and
and![]() . By given condition, there exists
. By given condition, there exists ![]() such that
such that![]() . Let
. Let![]() . As
. As ![]() uniformly, there exists
uniformly, there exists ![]() such that
such that ![]()
![]() . Choose
. Choose![]() . Then,
. Then, ![]() implies that there exist
implies that there exist ![]() such that
such that![]() . Further, as
. Further, as![]() ,
,![]() . Thus,
. Thus,![]() . Thus
. Thus![]() . As the proof can be replicated for any pair of non-empty open sets
. As the proof can be replicated for any pair of non-empty open sets![]() ,
, ![]() is transitive.
is transitive.
Result 2: Let ![]() be a compact metric space and let
be a compact metric space and let ![]() be a sequence of self maps on
be a sequence of self maps on ![]() converging uniformly to
converging uniformly to![]() . Then,
. Then, ![]() is weakly mixing if and only if for any pair of non-empty open sets
is weakly mixing if and only if for any pair of non-empty open sets![]() ,
, ![]() in
in![]() ,
,![]() .
.
Proof. Let ![]() be weakly mixing and let
be weakly mixing and let ![]() be two non-empty open sets in
be two non-empty open sets in![]() . As
. As ![]() is weakly mixing, there exists
is weakly mixing, there exists ![]() such that
such that![]() . Therefore, there exists
. Therefore, there exists ![]() such that
such that![]() . As
. As ![]() uniformly, there exists
uniformly, there exists ![]() such that
such that ![]()
![]() . Thus,
. Thus,![]() . Consequently
. Consequently![]() .
.
Conversely, let ![]() be non-empty open sets in
be non-empty open sets in![]() . Let
. Let ![]() and
and ![]() for
for![]() . Choose
. Choose ![]() such that
such that ![]() and
and![]() . Let
. Let ![]() and
and![]() . By given condition, there exists
. By given condition, there exists ![]() such that
such that![]() . Let
. Let ![]() . As
. As ![]() uniformly, there exists
uniformly, there exists ![]() such that
such that ![]()
![]() . Choose
. Choose![]() . Then,
. Then, ![]() implies that there exist
implies that there exist ![]() such that
such that![]() . Further, as
. Further, as![]() ,
,![]() . Thus,
. Thus,![]() . Thus
. Thus![]() . As the proof can be replicated for any collection of non-empty open sets in X,
. As the proof can be replicated for any collection of non-empty open sets in X, ![]() is weakly mixing.
is weakly mixing.
Corollary 1: Let ![]() be a compact metric space and let
be a compact metric space and let ![]() be a sequence of self maps on
be a sequence of self maps on ![]() converging uniformly to
converging uniformly to![]() . Then,
. Then, ![]() is topologically mixing if and only if for any pair of non-empty open
is topologically mixing if and only if for any pair of non-empty open
sets ![]() in
in![]() ,
, ![]() is cofinite.
is cofinite.
Proof. If ![]() is cofinite for a pair of open sets
is cofinite for a pair of open sets ![]() in
in![]() , then there exists a
, then there exists a ![]() such that
such that ![]() and
and ![]() interact under the map
interact under the map ![]() at time instant
at time instant![]() , for all
, for all![]() . Using previous result,
. Using previous result,![]() . However as
. However as ![]() is cofinite, such interaction happens for all
is cofinite, such interaction happens for all ![]() and hence
and hence ![]() for all
for all![]() . Thus
. Thus ![]() is topologically mixing.
is topologically mixing.
Result 3: Let ![]() be a compact metric space and let
be a compact metric space and let ![]() be a sequence of self maps on
be a sequence of self maps on ![]() converg-
converg-
ing uniformly to![]() . Then,
. Then, ![]() is sensitive if and only if there exists a
is sensitive if and only if there exists a ![]() such that for any non-empty open set
such that for any non-empty open set ![]() in
in![]() ,
,![]() .
.
Proof. Let ![]() be sensitive with sensitivity constant
be sensitive with sensitivity constant ![]() and let
and let ![]() be a non-empty open set in
be a non-empty open set in![]() . As
. As ![]() is sensitive, there exists
is sensitive, there exists ![]() and
and ![]() such that
such that![]() . As
. As ![]() uniformly,
uniformly,
there exists ![]() such that
such that![]() . Consequently
. Consequently ![]() for all
for all![]() . Thus
. Thus ![]() for all
for all![]() . Consequently,
. Consequently, ![]() and proof of the forward part is complete.
and proof of the forward part is complete.
Conversely, let ![]() be an arbitrary non-empty open set and let
be an arbitrary non-empty open set and let![]() . As
. As ![]() uniformly, there exists
uniformly, there exists ![]() such that
such that![]() ,
,![]() . Choose
. Choose![]() . Then, there exists
. Then, there exists ![]() such that
such that![]() . Also, as
. Also, as![]() ,
,![]() . Consequently,
. Consequently,![]() . As
. As ![]() was arbitrary,
was arbitrary, ![]() is sensitive.
is sensitive.
Corollary 2: Let ![]() be a compact metric space and let
be a compact metric space and let ![]() be a sequence of self maps on
be a sequence of self maps on ![]() converging uniformly to
converging uniformly to![]() . Then,
. Then, ![]() is strongly sensitive if and only if there exists a
is strongly sensitive if and only if there exists a ![]() such that for
such that for
any non-empty open set ![]() in
in![]() ,
, ![]() is cofinite.
is cofinite.
Proof. Similar
Result 4: Let ![]() be a compact metric space and let
be a compact metric space and let ![]() be a sequence of self maps on
be a sequence of self maps on ![]() converging uniformly to
converging uniformly to![]() . Then,
. Then, ![]() has dense set of periodic points if and only if for any non-empty open
has dense set of periodic points if and only if for any non-empty open
set ![]() in
in![]() ,
, ![]() , where
, where ![]() varies over all neighborhoods of
varies over all neighborhoods of![]() .
.
Proof. Let ![]() has dense set of periodic points and let
has dense set of periodic points and let ![]() be a non empty open set in
be a non empty open set in![]() . Let
. Let ![]() be periodic with period
be periodic with period![]() . As
. As ![]() uniformly,
uniformly, ![]() converges to
converges to![]() . Thus, for each neighborhood
. Thus, for each neighborhood ![]() of
of![]() , there exists
, there exists ![]() such that
such that ![]() for all
for all![]() . Thus,
. Thus, ![]() for all
for all ![]() which implies
which implies![]() . As the steps can be repeated for any neighborhood
. As the steps can be repeated for any neighborhood ![]() of
of![]() ,
,![]() . Consequently,
. Consequently,![]() .
.
Conversely, let ![]() be an arbitrary non-empty open set in
be an arbitrary non-empty open set in ![]() and let
and let![]() . Thus, there exists
. Thus, there exists ![]() such that for each neighborhood
such that for each neighborhood ![]() of
of![]() ,
, ![]() , i.e. every
, i.e. every
neighborhood ![]() of
of ![]() contains the tail of the sequence
contains the tail of the sequence![]() . Thus
. Thus ![]() converges to
converges to![]() . But as
. But as ![]() uniformly,
uniformly, ![]() and
and ![]() is a periodic point in
is a periodic point in![]() . As
. As ![]() was arbitrary,
was arbitrary, ![]() has a dense set of periodic points.
has a dense set of periodic points.
Acknowledgements
The author would like to thank the referees for their valuable comments and suggestions.