On No-Node Solutions of the Lazer-McKenna Suspension Bridge Models

Fanglei Wang, Kangbao Zhou

College of Science, Hohai University, Nanjing, China.

DOI: 10.4236/jamp.2015.37088                

Abstract

In this paper, we are concerned with the existence and multiplicity of no-node solutions of the Lazer-McKenna suspension bridge models by using the fixed point theorem in a cone.

Keywords

Differential Equations, Periodic Solution, Cone, Fixed Point Theorem

1. Introduction

In [1], the Lazer-McKenna suspension bridge models are proposed as following

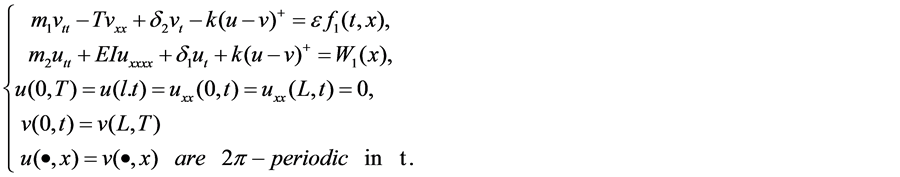
If we look for no-node solutions of the form 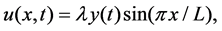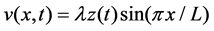and impose a forcing term of the form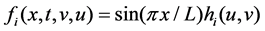, then via some computation, we can obtain the following system:

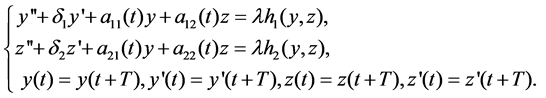(1)

In this paper, by combining the analysis of the sign of Green's functions for the linear damped equation, together with a famous fixed point theorem, we will obtain some existence results for (1) if the nonlinearities satisfy the following semipositone condition

(H) The function 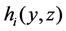is bounded below, and maybe change sign, namely, there exists a sufficiently large constant M > 0 such that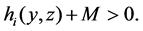

Such case is called as semipositone problems, see [2]. And one of the common techniques is the Krasnoselskii fixed point theorem on compression and expansion of cones.

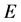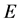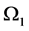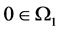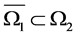Lemma 1.1 [3]. Let be a Banach space，and be a cone in. Assume， are open subsets of with, , Let 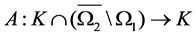be a completely continuous operator such that either

(i); or

(ii);

Then, has a fixed point in

2. Preliminaries

If the linear damped equation

(2)

is nonresonant, namely, its unique T-periodic solution is the trivial one, then as a consequence of Fredholm’s alternative in [4], the nonhomogeneous equation admits a unique T-periodic solution

which can be written as where G(t; s) is the Green’s function of (2). For convenience,

we will assume that the following standing hypothesis is satisfied throughout this paper:

(H1) are T-periodic functions such that the Green’s function, associated with the linear damped equation

is positive for all, and

(H2) are negative T-periodic functions, and satisfy:

Let E denote the Banach space with the norm for. Define K to a cone in E by where. Also, for r > 0 a positive number, let

If (H), (H1) and (H2) hold, let, (1) is transformed into

(3)

where is chosen such that

Let be a map, which defined by, where

t is straightforward to verify that the solution of (1) is equivalent to the fixed point Equation

Lemma 2.1 Assume that (H), (H1) and (H2) hold. Then is compact and continuous.

For convenience, define, for any.

Lemma 2.2 [2] Assume that (H), (H1) and (H2) hold. If, then, for i = 1, 2, the functions are continuous on, for, and

Lemma 2.3 [2] Assume that (H), (H1) and (H2) hold. If, then, for i = 1, 2, the functions are continuous on, for, and

3. Main Results

Theorem 3.1 Assume that (H), (H1) and (H2) hold.

(I) Then there exists a such that (1) has a positive periodic solution for

(II) If, then for an, (1) has a positive periodic solution;

(III) If, then (1) has two positive periodic solutions for all sufficiently small.

Proof. (I) On one hand, take R > 0 such that

Set Then, for each, we have

Then from the above inequalities, it follows that there exists a such that

Furthermore, for any, we obtain

In the similar way, there exists a, such that and we also have

So let us choose and we can obtain

On the other hand, from the condition for all, it follows that there is a sufficient small r > 0 such that for and where is chosen such that

Then, for any, we obtain

So we have

Therefore, from Lemma 1.1, it follows that the operator B has at least one fixed point in, for

(II) Since, then from Lemma 2.1, it follows that Define a function as By Lemma 2.5 in [2], it is easy to see that Thus by the definition, there is an such that where satisfying

Then, for each, we have

In the similar way, for any, we also have Furthermore, from The above inequalities, we get

Therefore, from Lemma 1.1, it follows that B has one fixed point in for any

(III) Since, then from Lemma 2.2, it follows that By the definition, there exists such that where is chosen such that

Choosing and for any, we have and

Thus from the above inequalities, we can get

Therefore, from Lemma 1.1, it follows that the operator B has at least two fixed points in and in. Namely, system (1) has two solutions for sufficiently small

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Lazer, A.C. and McKenna, P.J. (1990) Large-Amplitude Periodic Oscillations in Suspension Bridges: Some New Connections with Nonlinear Analysis. Siam Review, 32, 537-578. http://dx.doi.org/10.1137/1032120
[2]	Wang, H. (2009) Periodic Solutions to Non-Autonomous Second-Order Systems. Nonlinear Analysis: Theory, Methods & Applications, 71, 1271-1275. http://dx.doi.org/10.1016/j.na.2008.11.079
[3]	Dajun, G. and Lakshmikantham, V. (1988) Nonlinear Problems in Abstract Cones.
[4]	Chu, J., Fan, N. and Torres, P.J. (2012) Periodic Solutions for Second Order Singular Damped Differential Equations. Journal of Mathematical Analysis and Applications, 388, 665-675. http://dx.doi.org/10.1016/j.jmaa.2011.09.061