Block Unification Scheme for Elliptic, Telegraph, and Sine-Gordon Partial Differential Equations ()
1. Introduction
The method of lines approach which involves replacing the spatial derivatives with finite difference approximations is commonly used for solving PDEs; whereby, the PDE is transformed into systems of ODEs and solved by reliable ODE solvers (see Lambert [1] , Ramos and Vigo-Aguiar [2] , Brugnano and Trigiante [3] , D’Ambrosio and Paternoster [4] , and). Our objective is to convert the elliptic and hyperbolic PDEs into systems of ODEs by replacing the appropriate derivatives with central difference methods. The resulting systems of ODEs are then solved using an EBNUM via a block unification technique. We consider the two-dimensional PDE
 (1)
(1)
subject to Dirichlet or Neumann boundary conditions, where 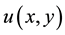 denotes the dependent variable, x and y are spatial variables,
denotes the dependent variable, x and y are spatial variables, 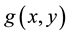 is a distributed source, and when
is a distributed source, and when , (1) becomes the two-dimensional convection diffusion equation given in Sun and Zhang [5] . We note that for
, (1) becomes the two-dimensional convection diffusion equation given in Sun and Zhang [5] . We note that for 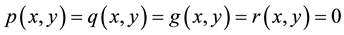 (1) is the Laplace equation, for
(1) is the Laplace equation, for 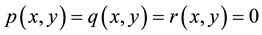 (1) is the Poisson equation, and for
(1) is the Poisson equation, and for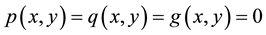 , (1) becomes the Helmoltz equation. The Sine- Gordon and telegraph equations can also be obtained from (1) by obvious notational modifications.
, (1) becomes the Helmoltz equation. The Sine- Gordon and telegraph equations can also be obtained from (1) by obvious notational modifications.
We invoke the method of lines approach in which for real numbers , we seek a solution in the strip
, we seek a solution in the strip  by first fixing the grid in the spatial variable x; then, approximating this spatial derivative using central difference methods, and finally solving the resulting system of second order time independent ODEs in the spatial variable y. Specifically, we discretize the x variable such that with mesh spacings
by first fixing the grid in the spatial variable x; then, approximating this spatial derivative using central difference methods, and finally solving the resulting system of second order time independent ODEs in the spatial variable y. Specifically, we discretize the x variable such that with mesh spacings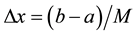 ,
,
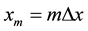 ,
,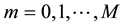 .
.
We then define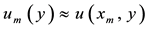 ,
, 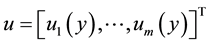 ,
, 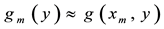 ,
,  , and replace the partial derivatives
, and replace the partial derivatives 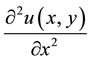 and
and ![]() occurring in (1) by their corresponding central difference approximations
occurring in (1) by their corresponding central difference approximations
![]() and.
and.
The problem (1) then leads to the resulting semi-discrete problem
![]() (2)
(2)
which can be written in the form
![]() (3)
(3)
subject to the boundary conditions
![]() ,
,
where![]() ,
, ![]() is a vector of constants, and A is an
is a vector of constants, and A is an ![]() matrix arising from the semi-discretized system (2) which is expressed in the form (3) and solved by a block unification method. We note that the EBNUM is an extended version of the method given in [6] for solving second order initial value problems.
matrix arising from the semi-discretized system (2) which is expressed in the form (3) and solved by a block unification method. We note that the EBNUM is an extended version of the method given in [6] for solving second order initial value problems.
The paper is organized as follows. In Section 2, we derive a continuous linear multistep method (LMM) which is used to formulate the EBNUM. The computational aspects of the method are given in Section 3. Numerical examples are given in Section 4 to show the accuracy of the method. Finally, the conclusion of the paper is discussed in Section 5.
2. Continuous LMM and EBNUM
In this section, we derive a continuous representation of a LMM which is used to generate the EBNUM. On the interval![]() , we approximate the exact solution by the interpolating function
, we approximate the exact solution by the interpolating function ![]() of the form
of the form
![]() (4)
(4)
where ![]() are parameters to be uniquely determined. Let
are parameters to be uniquely determined. Let ![]() denote the numerical approximation to the analytical solution at
denote the numerical approximation to the analytical solution at![]() ,
, ![]() ,
, ![]() , and n is a grid index. We impose that the interpolating function (4) coincides with the analytical solution at the points
, and n is a grid index. We impose that the interpolating function (4) coincides with the analytical solution at the points![]() ,
, ![]() to obtain the following pair of equations:
to obtain the following pair of equations:
![]() (5)
(5)
If the function (4) satisfies the scalar form of the differential Equation (3) at the points![]() , we obtain the following set of three equations:
, we obtain the following set of three equations:
![]() (6)
(6)
Thus, Equations (5) and (6) lead to a system involving the following five equations
![]()
which is solved with the aid of Mathematica to obtain![]() . The continuous LMM is constructed by substituting the values of
. The continuous LMM is constructed by substituting the values of ![]() into Equation (4) and after simplifying, the method is expressed in the form
into Equation (4) and after simplifying, the method is expressed in the form
![]() (7)
(7)
where![]() ,
, ![]() ,
, ![]() ,
, ![]() are continuous coefficients. The first derivative of (7) can easily be expressed as
are continuous coefficients. The first derivative of (7) can easily be expressed as
![]() (8)
(8)
The EBNUM is then obtained by evaluating (7) at ![]() and (8) at
and (8) at ![]()
![]() (9)
(9)
Remark 1 We note that the first two members of (9) were given in [7] and used for solving the special second order initial value problem.
The order of each method in (9) is given by the vector ![]() and local truncation errors associated with (9) are given by
and local truncation errors associated with (9) are given by
![]() (10)
(10)
The method (9) can be expressed in block form as
![]() (11)
(11)
where the positive integer ![]() is the number of blocks,
is the number of blocks, ![]() is the step number,
is the step number,
![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and![]() ,
, ![]() ,
, ![]() , and
, and ![]() are matrices each of dimension 4 whose entries are
are matrices each of dimension 4 whose entries are
given by the coefficients of (9).
Let the local truncation error be defined by![]() , and let the exact form of the system is given by (11) be defined as
, and let the exact form of the system is given by (11) be defined as
![]() (12)
(12)
where
![]() ,
,
![]()
![]() ,
,
![]()
Theorem 2 Let ![]() be an approximation of the solution vector
be an approximation of the solution vector ![]() for the system obtained on the interval
for the system obtained on the interval
![]() from the method (11). If
from the method (11). If![]() ,
, ![]() , where the exact solution
, where the exact solution ![]() is several times differentiable on
is several times differentiable on ![]() and if
and if![]() , then, the BLMM is convergent of order 4, which implies that
, then, the BLMM is convergent of order 4, which implies that![]() .
.
Proof. See Jator [8] .
Stability
The linear-stability of (11) is discussed by applying the method to the test equation![]() , where
, where ![]() is a real constant (see [9] ). Letting
is a real constant (see [9] ). Letting![]() , it is easily shown that the application of (11) to the test equation yields
, it is easily shown that the application of (11) to the test equation yields
![]() (13)
(13)
where the matrix ![]() is the amplification matrix which determines the stability of the method.
is the amplification matrix which determines the stability of the method.
Definition 3 Let ![]() be the spectral radius, the interval of stability is an interval throughout which
be the spectral radius, the interval of stability is an interval throughout which![]() . We then define the interval of periodicity as the largest interval
. We then define the interval of periodicity as the largest interval ![]() such that
such that ![]() for all steplengths
for all steplengths![]() . Suppose
. Suppose ![]() is finite, and
is finite, and ![]() also holds for
also holds for![]() , for
, for![]() , then,
, then, ![]() is the secondary interval of periodicity (see [10] ).
is the secondary interval of periodicity (see [10] ).
Remark 4 We found that ![]() if
if![]() , hence the stability interval for the EBNUM is
, hence the stability interval for the EBNUM is![]() ;
;
which is twice the stability interval of the standard Numerov method. In this case, the interval of stability is the same as the interval of periodicity.
3. Computational Aspects via Block Unification
Recall that the semi-discretization of (1) is initially performed on the partition
![]()
![]() . The resulting system of ODEs (3) is then solved on the partition
. The resulting system of ODEs (3) is then solved on the partition![]() .
.
Next, we summarize the block unification algorithm. Let ![]() be the number of blocks and let
be the number of blocks and let ![]() be the individual blocks obtained on the rectangles
be the individual blocks obtained on the rectangles![]() ; then, the blocks are unified and solved as follows:
; then, the blocks are unified and solved as follows:
Step 1: Use the block extension of (11) for ![]() to obtain
to obtain ![]() on the rectangle
on the rectangle![]() , for
, for![]() ,
, ![]() is obtained on the rectangle
is obtained on the rectangle![]() , and on the rectangles
, and on the rectangles![]() , for
, for![]() ,
, ![]() , we obtain
, we obtain![]() .
.
Step 2: The blocks are unified to form a system given by![]() . The system is then simultaneously solved to obtain approximations
. The system is then simultaneously solved to obtain approximations![]() .
.
Step 3: The solution of (1) is approximated by the solutions in step 2 as![]() ,
,![]() .
.
We emphasize that the block unification technique leads to a single matrix of finite difference equations, which is solved to provide all the solutions of (1) on the entire grid given by the rectangle![]() . We note that the computations were carried out using a written code in Mathematica 10.0.
. We note that the computations were carried out using a written code in Mathematica 10.0.
4. Numerical Examples
4.1. Elliptic PDEs
In this subsection, the performance of the EBNUM is tested on five problems, which include the Poisson equation, Laplace equation subject to Neumann boundary conditions, Laplace equation subject to Dirichlet boundary conditions, Helmoltz equation, and the two-dimensional convection diffusion equation. In all the figures, the EBNUM is represented by uapprox and the exact solution is represented by uexact.
Example 5 As our first test example, we solve the given Poisson equation (see Burden and Faires [11] ).
![]()
![]() ,
,
![]()
The exact solution is given by![]() .
.
This example was chosen to demonstrate that the EBNUM can be used to solve the Poisson equation with Dirichlet boundary conditions. The results produced by the EBNUM are accurate as shown by the graphical evidence given in Figure 1.
Example 6 As our second test example, we solve the given Laplace equation subject to Neumann boundary conditions (see Zill and Cullen [12] ).
![]()
![]() ,
,
![]()
The exact solution is given by![]() .
.
This example was chosen to illustrate that the EBNUM is cable of solving the Laplace equation with Neumann boundary conditions. The results produced by the EBNUM are accurate as shown by the graphical evidence given in Figure 2.
Example 7 As our third test example, we solve the given Laplace equation subject to Dirichlet boundary conditions (see Zill and Cullen [12] ).
![]()
![]()
Figure 1. Approximate and exact solutions for example 4.1, h = 1/64; Δx = 1/64.
![]()
Figure 2. Approximate and exact solutions for example 4.2, h = 1/128; Δx = 1/128.
![]() ,
,
![]()
The exact solution is given by
![]()
This example was chosen to demonstrate the performance of the EBNUM on the Laplace equation with Dirichlet boundary conditions. We truncated the exact solution at 50, since the exact solution is an infinite series. The results produced by the EBNUM are accurate as shown by the graphical evidence given in Figure 3.
Example 8 We consider the given two-dimensional Helmoltz equation (see Cheney [13] ).
![]()
The exact solution is given by![]() .
.
The Dirichlet boundary conditions are chosen accordingly. This example was chosen to demonstrate that the EBNUM can be used to solve the Helmoltz equation. The results produced by the EBNUM are accurate as shown by the graphical evidence given in Figure 4.
Example 9 We consider the given two-dimensional convection diffusion equation (see Sun and Zhang [5] ).
![]()
![]()
Figure 3. Approximate and exact solutions for example 4.3, h = 1/128; Δx = 1/128.
The exact solution is given by ![]() and the convection coefficients are
and the convection coefficients are ![]() and
and![]() .
.
The Dirichlet boundary conditions and ![]() are chosen accordingly. This example was chosen to demonstrate that the EBNUM can be used to solve the two-dimensional convection diffusion equation. The results produced by the EBNUM are accurate as shown by the graphical evidence given in Figure 5.
are chosen accordingly. This example was chosen to demonstrate that the EBNUM can be used to solve the two-dimensional convection diffusion equation. The results produced by the EBNUM are accurate as shown by the graphical evidence given in Figure 5.
![]()
Figure 4. Approximate and exact solutions for example 4.4, h = 1/128; Δx = 1/128.
![]()
Figure 5. Approximate and exact solutions for example 4.5, h = 1/128; Δx = 1/128.
4.2. Hyperbolic PDEs
Example 10 We consider the following one-dimensional nonlinear undamped Sine-Gordon equation given in Dehghan and Shokri [14] )
![]()
![]() ,
,
![]() .
.
The exact solution is given by![]() ,
,
C is the velocity of the solitary wave, and the boundary conditions are given according. The problem is solved for![]() ,
, ![]() , and
, and![]() . This example was chosen to demonstrate that the EBNUM can be used to solve the Sine-Gordon equation. The results produced by the EBNUM are accurate as shown by the graphical evidence given in Figure 6.
. This example was chosen to demonstrate that the EBNUM can be used to solve the Sine-Gordon equation. The results produced by the EBNUM are accurate as shown by the graphical evidence given in Figure 6.
Example 11 We consider the given Telegraph equation (see Ding et al. [15] ).
![]()
![]()
Figure 6. Approximate and exact solutions for example 4.6, h = 1/50; Δx = 1/150.
The exact solution is given by![]() .
.
The boundary conditions are chosen accordingly. This example was chosen to demonstrate that the EBNUM can be used to solve the telegraph equation. The results produced by the EBNUM are accurate as shown by the graphical evidence given in Figure 7.
4.3. Comparison of EBNUM and FDM
In this subsection, we compare the errors ![]() and CPU time in seconds for
and CPU time in seconds for ![]() of the EBNUM and FDM for all the examples.
of the EBNUM and FDM for all the examples.
5. Conclusion
A block unification method based on the EBNUM is proposed and applied to elliptic and hyperbplic PDEs via the method of lines technique. It is shown that the method is very flexible as it can be applied to solve a variety of elliptic and hyperbolic PDEs with either Dirichlet or Neumann boundary conditions. The method is also shown to have both accuracy and speed advantages when compared with the FDM (see Table 1). Our future re-
![]()
Figure 7. Approximate and exact solutions for example 4.7, h = 1/16; Δx = 1/16.
![]()
Table 1. Comparison of errors and CPU time in seconds.
search will be to search for higher order LMMs that can solve the general forms of elliptic and hyperbolic PDEs.