Saint-Venant Equations and Friction Law for Modelling Self-Channeling Granular Flows: From Analogue to Numerical Simulation ()
1. Introduction
Rock avalanches are rare but catastrophic events in which large volume of granular material (>106 m3) flows downslope at high velocities (up to 100 m/s) [1] . They can cover areas over 0.1 km2 and reach great and unusual distances of runout. They are costly in term of human life losses and can have consequent impact in the environmental and the economic system. Rock avalanches or Sturzstroms as called by Heim [2] are defined as an extremely rapid, massive, flow-like motion of rock fragments derived from a bed-rock failure and which exhibits greater mobility than could be predicted using frictional models [3] . The excess travel distance of these masses was first observed by Heim [2] and quoted by Hsü [4] who proposed that the runout depends directly on the volume of the flowing mass and suggests that the propagation follows more the characteristics of fluid flow rather than the sliding accumulation of debris. This volume influence was also investigated by Scheidegger [5] and Nicoletti and Sorriso-Valvo [6] . Other theories were proposed to explain this excess travel distance as the transfer of momentum between the rear and the front of the mass [7] , the fragmentation [8] [9] or that the frequency of collisions could cause a longer runout [10] [11] . Other theories proposed to reduce the basal friction, as proposed by Kent [12] , where entrapped and compressed air fluidizes the landslide or a layer of a trapped air at the base. As these events are rare, laboratory experiments can give crucial information about their propagation and the influence of parameters on the mobility under idealized conditions (i.e. [8] [9] [13] -[16] ). These laboratory experiments are widely used to calibrate numerical models.
In natural sciences, phenomenon like landslides, debris or pyroclastic flows are associated to large scale to large-scale flow of grains [17] . Recent studies proposed numerical model of frictional flows based on the Saint- Venant equations to simulate such phenomenon [18] -[25] .
As landslides are complex phenomena that cannot be described with simple hydrodynamic assumptions and involve different materials (plastic, fluid, rigid components) the concept of equivalent fluid approach is useful to describe their behaviour. This equivalent fluid is supposed incompressible and is governed by frictional rheology. The numerical model proposed in this work is based on the continuum mechanics approach considering that the thickness and length of the mass is greater than the particles composing the mass. The avalanche is then described from a eulerian point of view within a continuum framework as single phase of incompressible granular material following a Mohr-Coulomb friction law. In order to calibrate the numerical model, analogue experiments were carried out in laboratory on simple inclined plane geometry.
2. Methodology
In order to constrain and understand the different parameters constraining a granular flow, a detail laboratory campaign were carried out. The experimental setup is a simple aluminium slope geometry composed of two distinct parts (Figure 1): 1) a 90 × 70 cm slope with an inclination α which can be precisely controlled, 2) a 120 cm
![]()
Figure 1. Sketch of the setup. The mass is represented by the grey dot. G, N and S are the forces acting on the mass motion and are respectively the Gravity, Normal stress and Shear at the base. “θ” is the slope, “L the slope length,” “l the surface of deposition length and w the width of the setup.
long horizontal surface (surface of deposition) connected to the slope. Both slope and surface of deposition are made of aluminium in order to have low basal friction. The setup includes a starting box (11 × 8 × 7 cm) where the loose material is enclosed at the beginning of the experiment. This box is separated of the setup to avoid vibrations during the release of the material and is quickly separated of the slope means of a retractile jack. When the trap opens, the mass is released along a slope and deposits on a horizontal plane. The granular material is angular and calibrated carborandum sand (SiC, density = 3.21 g/cm3) with a mean grainsize of 2605 µm. The choice of carborandum is to avoid the static electricity effect that can falsify the analysis by means of a cohesive effect. In addition the angular shape is to have similitudes with natural material.
A volume of 400 cm3 of granular material is poured in the starting box and the setup is adjusted to have a slope angle of 45˚ and a height of fall of 50 cm. Then, the mass is released and flow freely on the slope without any lateral constrains until it reached the surface of deposition, where it is slowed down and stopped. The flow is recorded by a high speed camera to see how the granular flow behaves during its motion. Once the mass stopped, the deposit was manually measured (length, width). Then it was scanned by a 3D digitizer (Konica Minolta vivid 9i micro-Lidar) in order to get a 3D geometrical model. Based on the 3D model, the profile of the deposit can be drawn along the flow direction, through the center of mass. In order to have significant results, the experiment is repeated three times. The results presented in this paper are the mean average of each measured parameters. Numerical tests were carried on the Matlab software with the same physical constants than analogue tests. The volume was set to 400 cm3 and positioned at the center of the ramp at a height of fall of 50 cm. The slope angle θ is 45˚. The density ρ of the material is 3.21 g/cm3 and the basal friction μ is 0.6.
3. Numerical Model
3.1. Continuum Mechanics Approach
A granular flow consists into an assemblage of discrete particles of different size (from blocks to dust) but if the dimension of the flowing mass are bigger than the dimensions of the standard particles, then the material can be treated as continuum. Therefore, the mass can be associated to an apparent equivalent fluid with rheological properties such that the bulk behavior of the flowing body simulates the expected bulk behavior of the landslide [23] . To summarize, the granular flow is described within a continuum theoretical framework as a single-phase, incompressible material with a constant density [19] [25] -[27] . As the lateral extension of the mass is large compared to the thickness of the layer, the use of the depth-average equations are used to describe the flow. The derivation proceeds from an Eulerian frame of reference. In each direction, the variation in time between two points can be considered as the integration of the velocities at each of these points and the sum of the forces applied in these 2 points [26] :
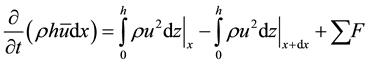 (1)
(1)
where ρ is the density, h the local thickness, and u corresponds to velocity.
The integrals represent the variation over the x direction of the square velocity and Equation (1) can therefore be rewritten as [26] :
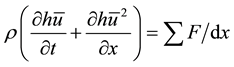 (2)
(2)
Along the slope θ, the sum of the forces 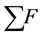 is composed of the four following elements [28] :
is composed of the four following elements [28] :
・ The normal stress vector 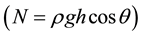
・ The driven gravity force parallel to the flow direction 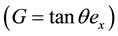
・ The shear at the base and is opposed to the motion of the mass 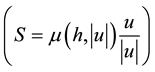
・ The pressure force link to the thickness and to the earth pressure coefficient 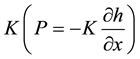
This allows by replacing the sum in Equation (2) by its elements to obtain the momentum conservation equation on the x dimension [28] :
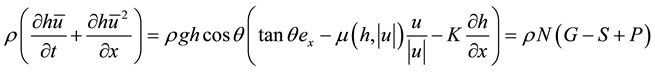 (3)
(3)
Generalizing this equation over the y dimension with the same method and simplifying the density present on each side of the equation gives the momentum conservation equation we will use for the model, which we write here together with the mass conservation equation (modified after [28] ):
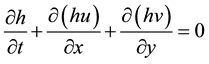 (4)
(4)
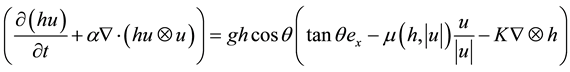 (5)
(5)
where ρ is the density and is constant, g the terrestrial gravity, h the local thickness, θ the slope angle, µ the basal friction coefficient, K the earth pressure coefficient and α the acceleration term [28] (as the flow of a granular
mass is close to a linear profile, then 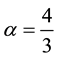 after [28] ). u and v correspond to depth averaged velocity and can
after [28] ). u and v correspond to depth averaged velocity and can
be expressed as followed [28] : .
.
The Earth pressure coefficient K was introduced by Savage and Hutter [24] to describe the state of stress depending upon whether an element of material is being elongated or compressed in the direction parallel to the bed. The coefficient K can then be active or passive, dependent whether the motion is dilatational or compressional: he represents the ration of the vertical normal stress to the horizontal stress and it can be calculated from the Mohr-Coulomb model for quasi-static deformation. However, material used to simulate granular flows on rough surfaces behaves more like a fluid. Moreover, numerical simulations tend to show that vertical and horizontal stresses are equal [28] . In this study, we used K = 1, corresponding to the isotropy of normal stress. In their study, Pouliquen and Forterre [28] showed that changing K does not influence the propagation.
The conventional method in computational fluid dynamics is the Eularian approach: this numerical model is described following this framework.
3.2. Frictional Law and Flow Conditions
As mentioned in §3.1, we assumed the isotropy of normal stresses (σxx= σyy= σzz). The Coulomb-type behavior can be written as follow [19] :
 (6)
(6)
 (7)
(7)
where 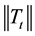 is the norm of the tangential traction T,
is the norm of the tangential traction T, ![]() and σc defines the upper bound of the admissible stress (
and σc defines the upper bound of the admissible stress (![]() , after [19] ). This means that, if
, after [19] ). This means that, if![]() , then the mass flows following the dynamical equations whereas if
, then the mass flows following the dynamical equations whereas if![]() , the mass stops.
, the mass stops.
In their work, [27] [28] highlighted the existence of two critical angles to describe the onset of a granular flow. Both are dependent of the initial thickness h of the layer. The mass starts to flow when the inclination reaches a value of θstart(h) and stops when the slope decreases to θstop(h). They proposed an empirical friction law ![]() (where
(where![]() ) as a function of the Froude number
) as a function of the Froude number![]() . The friction coefficient can be written as followed [28] :
. The friction coefficient can be written as followed [28] :
If Fr > β:
![]() (8)
(8)
If 0 < Fr < β:
![]() (9)
(9)
If Fr = 0:
![]() (10)
(10)
where β is a constant equal to 0.136 [28] . This constant was calculated by Pouliquen [27] and it is independent of the slope angle, the size of the grains and the roughness of the path. In its work, he illustrated the Froude number ![]() as a linear function of h/hstop and this value of β correspond to the best fit. hstop is there the critical thickness when the flow stops. The power γ seems to have little influence on the model and was chosen equal to 10−3 according Pouliquen and Forterre [28] .
as a linear function of h/hstop and this value of β correspond to the best fit. hstop is there the critical thickness when the flow stops. The power γ seems to have little influence on the model and was chosen equal to 10−3 according Pouliquen and Forterre [28] .
3.3. Numerical Model
The model is based on the finite volume approach. F was calculates in the continuum mechanics section (Equation (3)) and obtained the combination of normal stress, gravity, shear forces and internal pression as following:
![]() (11)
(11)
This expression is valid for our x dimension and can be modified for the y dimension by taking out the gravity as there is no level difference in this direction for the model. Combining these into a two dimension vectorial expression (t, x, y) and replacing the forces with their calculated expressions gives the following relation:
![]() (12)
(12)
The Equations (1) and (2) are rewritten in the following conservative form, as proposed by Pouliquen and Forterre [28] :
![]() (13)
(13)
where U, Bx and By are vectors depending on the thickness h and the velocities u and v.
The flux q in the model is defined by a U vector with q = hu, lets us obtain:
![]() (14)
(14)
The mass going downslope is driven by the Bx and By vectors, each in one direction over the dimensions t, x, y. These vectors are defined as following:
![]() (15)
(15)
In these expressions the main driver in each direction is given by the corresponding dimension of the vector taking into account simultaneously the acceleration due to the flux and the gravity effect. To ensure the numerical stability of this system, we applied the Lax-Friedrichs scheme (Appendix A).
For each iteration, the velocities are updated as followed:
![]() (16)
(16)
with i representing each cell of the grid and t the time step.
3.4. Boundary and Initial Conditions
To ensure the stability of the system and avoid the loss of mass outside of the system, there is a need of boundary conditions for Bx and By. These conditions are that there is no driving force on the border of the simulated slope, i.e. the time values for Bx and By at the boundaries are set to zero:
![]() (17)
(17)
where L is the length of the slope, l the length of the surface of deposition and w the width of the setup (Figure 1).
As initial conditions, at the beginning of the simulation, the mass is in place without moving. All parameters (velocities, forces) are set to zero.
4. Results
4.1. Influence of the Friction Law on the Numerical Model
In order to see how the fiction law influenced the runout, two models were carried out with same physical constants (volume = 400 cm3, θ = 45˚, ρ = 3.21 g/cm3 and μ = 0.6), same resolution (600 elements in x, 200 elements in y), and 5000 iterations. The first trial was made without any friction law. In the second trial the Coulomb-like friction law was added. Figure 2 compares both cases at same time steps. During the mass collapse (Figure 2(a)) as well as the flow along the slope (Figure 2(b)), the propagation of the mass in both tests is similar. Major differences appeared when the mass reached the surface of deposition (Figure 2(c)). By definition, a mass without friction law does not stop and continue to spread laterally. This is observable in the numerical test without friction. On the contrary, the experiment with the friction is stopped once the velocity equals 0 (Figure 2(d)). Moreover, the result without friction law is more diffusive. The results are summarized in Table 1.
4.2. Influence of the Resolution on the Numerical Model
Another parameter influencing the numerical runout is the numerical resolution. In order to see how it influences the mass propagation, two numerical tests were carried out with the same physical constants (volume = 400 cm3, θ = 45˚, ρ = 3.21 g/cm3 and μ = 0.6), 5000 iterations and without frictional law. The first one has a low resolution (300 elements in x, 100 elements in y) whereas the second one has a higher resolution (600 elements in x, 200 elements in y). Figure 3 shows that the resolution is a crucial parameter influencing the diffusion. The diffusion phenomenon is visible as early as the mass collapses (Figure 3(a)). It is increasing during the flow (Figure 3(b)) and is maximal when the mass stops (Figure 3(c)). The runout obtained with a low resolution is greater than the one obtained with higher resolution. The results are summarized in Table 1.
4.3. Comparison between the Analogue Experiment and Numerical Model
On this paper, only the experiments carried with a slope angle of 45˚ and a height of fall of 50 cm are presented. Figure 4 shows the flow of the granular mass. First, the trap opens and the material is released (Figures 4(a)-(b)). Then, it flows freely on the slope and where it spreads laterally (Figure 4(c)). When the front of the mass hits the surface of deposition (Figure 4(d)), the lateral extension is maximal and the velocity of the flow starts to slow down (Figure 4(e)). Finally, all the granular material is on the surface of deposition and the mass is stopped (Figure 4(f)). The elapsed time between Figure 4(a) and Figure 4(f) is 3.8 seconds. By dividing the distance traveled by the mass by the elapsed time, we obtained an average velocity of 0.2 m/s.
To reproduce the analogue experiments, similar parameters were used for the numerical model: the volume is set to 400 cm3, the slope θ to 45˚, the density ρ is 3.21 g/cm3, the basal friction μ is 0.6 and with friction law. The resolution is 600 elements in x, 200 elements in y and the number of iterations is 5000. Figure 2 presents the numerical simulation of the flow at different time step. First, the mass is set at the center of the slope (Figure 4(g)): this position corresponds to the enclosed granular material in the analogue experiments (Figure 4(a)). Then the mass collapses (Figure 4(h)): this corresponds to the mass released in the analogue experiment (Figure 4(b)). After the collapse, the mass starts to flow, increasing its velocity and extending laterally (Figures 4(h)-(i)). As for the analogue granular flow, the maximum of the lateral extension is reached once the mass hits
![]()
Figure 2. Influence of the friction on the numerical runout (V = 400 cm3, θ = 45˚, ρ = 3.21 g/cm3 and μ = 0.6).
![]()
Figure 3. Influence of the numerical resolution on the propagation (V = 400 cm3, θ = 45˚, ρ = 3.21 g/cm3 and μ = 0.6).
the surface of deposition (Figure 4(j)). Once the surface of deposition is hit, the velocity decreases rapidly. The mass continues to propagate on the surface of deposition (Figure 4(k)) until the friction is too high leading to the velocity deceleration and the stop of the mass (Figure 4(l)). In the model, we can see that the mass is not constrained and is free to extend laterally. The results are summarized in Table 1.
Figure 5 compares both deposits, numerical and analogue. The length of the granular deposit is 25.3 cm and its width is 36.6 cm (Figure 5(a)). For the numerical deposit, we have a length of 31.25 cm and a width of 38.6 cm. Cross sections were drawn along the flow direction through the center of the deposit (Figures 5(c)-(d)). The cross section obtained with the laboratory deposit (Figure 5(a)) has an elongated shape with a thickness presenting no important variations. On the contrary, the cross section of the numerical deposit has a different shape, where the thickness is greater close the slope-break and gently decreases.
The velocity profile obtained with the numerical experiments (Figure 6(a)) shows that the velocity rapidly increases when the mass collapses and flows and decreases when the mass hits the surface of deposition until it stops.
![]()
Figure 4. (a)-(f) are pictures of an analogue experiments from the release of the mass until the deposition. The time between each picture is 0.6 s; (g)-(l) represent the numerical propagation at similar stages than the analogue propagation. (V = 400 cm3, θ = 45˚, ρ = 3.21 g/cm3 and μ = 0.6).
![]()
Figure 5. (a) Result of the analogue experiment; (b) Result of the numerical model; (c) Cross section of the analogue deposit deduced from the 3D model of the deposit; (d) Cross section of the numerical deposit (V = 400 cm3, θ = 45˚, ρ = 3.21 g/cm3 and μ = 0.6).
![]()
Figure 6. (a) Numerical velocity profile; (b) Mass conservation profile.
![]()
Table 1. Results of the height, length and width of analogue and numerical deposits for 5000 iterations. Maximum velocity is only obtained with the numerical simulation. FL is for friction law. Low resolution: 300 elements in x, 100 elements in y. High resolution: 600 elements in x, 200 elements in y.
During the simulation, the mass is verified (Figure 6(b)).
5. Discussion and Conclusions
As it is presented in this paper, the flow of a granular mass along a planar surface can be described in a depth- average description by introducing a friction law. As it is shown in Figure 4, the spreading of a granular flow is predicted by the model from the release of a uniform granular mass initially static up to the deposit.
Table 1 summarizes and compares the results obtained with the analogue experiment with those get numerically. The differences between numerical and analogical length, width and height are probably caused by the manual measurement in laboratory. Indeed, for the experiments, only the distinct part of the front mass was measured: particles separated by a distance greater than their own diameter were not considered as part of the deposit. The mean numerical velocity is 0.3 m/s which is higher compare to the one estimated during the analogue modeling (0.2 m/s).
The numerical model has been extended to model simple granular flows on a simple topography. The code analysis the propagation of a flow with an earth friction coefficient K equals 1 as it does not provide better agreement for the propagation [28] and the system has been described using a Coulomb-type friction law. The Coulomb-type friction law describes the interaction between the basal layer, the granular mass and topography and is closely linked to the starting and stopping angle (Equations (10)-(12)).
To summarize, the main points resulting from this study are the following:
1) It is well known that Coulomb-type like friction law in a depth average description allowed simulating the flow. In our model, an initial static layer is simulated until to its deposition when the velocity equals 0;
2) The granular mass flows freely along the slope and the surface of deposition: contrary to previous work, no topographic constraints or special border conditions are required to enable this self-channelization;
3) Once the front of the mass reaches the slope break, the whole mass slows down until its stops completely on the surface of deposition. At this point, the velocity equals 0;
4) Even if the velocity is higher with numerical simulation, numerical and analogue modelling give the same magnitude of velocities;
5) During the whole simulation, the mass is conserved;
6) The numerical model is validated through analogue modeling. With same parameters and conditions, the results of the numerical model confirms to those observed with laboratory experiments;
7) Simulations on simple slope geometry allowed us to test the capability and limitations of the numerical model.
The main aim of this work was to have a numerical tool applicable to back analysis of laboratory experiments and able to predict the propagation and the deposit shape of a granular mass along a slope. The results are promising, as laboratory experiments are correctly described with this model, and therefore further developments on this work are required to improve the imprecision linked to the numerical artifacts and provide a useful tool for real cases back analysis. The application of such model to natural hazard will improve risk assessment and provide tools to understand the behaviour of rock avalanches.
Acknowledgements
The authors are grateful to Martin Franz and Remo Gygax for their precious advices and help and to Martin Aeberhardt for his constructive comments that improved the manuscript. Many thanks to the reviewers for critical comments on the manuscript
Annexe A: Lax-Friedrichs Scheme
To computes the Bx and By vectors (Equation (15)), the Lax-Friedrichs scheme was used:
![]() (18)
(18)
![]() (19)
(19)
After [29] , the Lax-Friedrichs method is the most robust. Indeed, with this method, diffusive problems observed during the simulations disappear by increasing the resolution. Moreover, it has advantage of capturing correct propagation velocities, being non-oscillatory, being relatively fast and very easy to implement.