Fast Time-Varying Channel Model Research for Data Processing of Wireless ()
1. Introduction
Broadband mobile communication transmission is changing people’s life. Due to complexity and uncertainty of the mobile communication network environment, higher requirements and challenges are put forward to realize the high-speed broadband data transmission. Through the analysis of the lack of existing communication model, setting up new mathematical models will be a good role in promotion to improve the channel capacity, increase the information transmission rate and reduce the error rate. In a communication system, transmitter transmits signals to the receiver through channel which inevitably brings about the noise interference. The noise-contami- nated signal is reasonably decoded by the receiving end, getting the right information to complete the information transmission. There are more than one signal transmission path between the sending and receiving wireless channel [1] .
The model tree was first proposed by Quinlan in 1992. It is a classical model for regression tasks. The model tree is different from the regression tree which is proposed by Breiman. The regression tree has real value only in the leaf node of the decision tree, and it will give the real value to the example which falls into the corresponding leaf node. The model tree constructs multivariate linear regression model. Thus, the model tree is similar to the piecewise linear model. Through the analysis of the measured data in this paper, the real and imaginary parts are discussed respectively. The real and imaginary parts of the data are highly cyclical from the analysis. The Fourier series has a good fitting for periodic data. Accordingly, the model tree of basis function method based on Fourier series is proposed, as shown in Figure 1. Model tree method is the improvement of regression tree analysis. No longer using values for node in the tree structure characteristics, the method replaces them by the corresponding basis function. Compare the dispersions between the data before and after branching and the original data to decide whether or not to branch and carry out the pre-pruning treatment, in order to reduce the complexity of tree structure. Basis function applied here is four-order Fourier series. When the Fourier coefficients are calculated, the Gauss elimination method is implemented for solving equations. Data file 1 is the impulse response sequence of a channel, developed from the data change relation. Pretreat the impulse response sequence, separating the real and imaginary parts. The real and imaginary parts are highly cyclical. Fitting processing is conducted by the Fourier series in this paper. In view of the fact that the General Fourier series requires a very high order to achieve better prediction, I propose the segmented Fourier series based on model tree method so as to reduce the order of Fourier series and also the complexity of the algorithm.
2. Partial Modeling of Complex Data―Regression Tree of Fourier Model
There are a large number of model examples solved through statistical probability model and basis expansion method, but they are too complex to reach the conclusions quickly [2] . This paper presents a regression tree method of Fourier model, as shown in Figure 2. Regression tree belongs to the improved method of decision tree. Generally speaking, the decision tree requires that data segmentation should be cut into small data set until they can’t be subdivided. Decision tree is a greedy algorithm, and with the given eigen values to partition the data, it will make the best choice in a given time but don’t care about whether the global optimum is reached or not. Data can be cut through the tree structure for complex data model, how to carry out effective data segmentation depends on the modeling way of the leaf node [3] .
2.1. Data Preprocessing
The data file 1 is the tested impulse function values of a channel (velocity 180 Km/h, carrier frequency 3 GHz, channel sampling frequency 200 KHz). Because this kind of impulse response value is a set of plural, it is complex and time-consuming to build the model via the perspective of channel modeling. The paper starts with the data relationship [4] . The data file 1 is a series of impulse response sequences with an increasement during each unit sampling time, and the values are plural. I separate the real and imaginary parts and draw respectively the corresponding diagram.
Figure 3 and Figure 4 show that, whether the imaginary or real parts, they have obvious periodicity with respect to time. The better approach of fitting periodic data is to use the Fourier series method.
2.2. Fourier Series Approximation
Any periodic function can be reconstructed with the infinite series of the sine and cosine function (because of their orthogonality, I select the sine and cosine function as the basis function). Fourier series is a special trigonometric series. I use the Fourier least square method, assuming 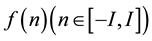 is on behalf of the original signal, whose Fourier series approximation is:
is on behalf of the original signal, whose Fourier series approximation is:
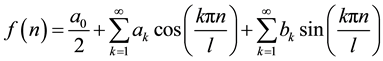 (1)
(1)
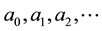 and
and  are the Fourier factors of
are the Fourier factors of , K is the harmonic coefficient with the approximation degree of
, K is the harmonic coefficient with the approximation degree of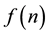 . Fundamental frequency
. Fundamental frequency 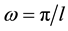 and Fourier factor
and Fourier factor 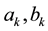 are calculated using the following algorithm:
are calculated using the following algorithm:
Counting u1 and u2:
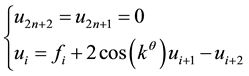 (2)
(2)
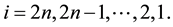
 (3)
(3)
2n is the length of signal, u1 and u2 are temporary variables, 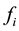 represents the signal value at
represents the signal value at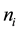 .
.
This recursive numerical analysis algorithm is superior in solving the Fourier faction. The Fourier series of higher order in this paper will be solved via this method. The column main element method of Gauss elimination method is used for solving iterative equations [5] . High frequency of noise signal has a great impact on source signal. This paper uses the absolute value of difference between the fitted signal and source signal to measure the error [6] :
 (4)
(4)
![]() and
and ![]() represent the i data and fitting data respectively.
represent the i data and fitting data respectively.
![]()
Figure 3. The impulse response of imaginary parts (velocity 180 Km/h).
![]()
Figure 4. The impulse response of real parts (velocity 180 Km/h).
2.3. Model Tree
The tree structure is used for data modeling. This paper proposes that the segmented Fourier series will be applied for fitting in addition to setting the leaf nodes simply as constant or linear function. This so-called segmentation refers to that the model tree is composed of several segments of Fourier series. The advantage of model tree compared to other machine learning models is with a more easily understandable outcome. Obviously, the segmented Fourier series are clear and easy to understand.
Model tree is a predictive model, representing a mapping relationship between object attribute and object value. Each node in the tree is representation of an object. Each branch path represents the possible attribute value while each leaf node corresponds to the value of the object represented by all the paths from root node to leaf node. The decision tree has only one single output, thus independent decision trees can be built to deal with different output if the desired outcome are more than one outputs. The decision tree is a frequently used technique in data mining, and it can be used to analyze the data as well as for prediction. This paper will take the Fourier series model as the basis function for model tree.
2.4. Pre-Pruning
Avoiding over fitting is realized mainly through the tree pruning which includes pre-pruning and post-pruning. The former is to find a wrong result, then stop the splitting process of the node. The latter is to let it keep splitting up till its limit, and then find the branches of no significance. But the computational cost of post-pruning is much greater than pre-pruning method, especially with a large sample set.
The Fourier series equation is used as the model tree in the process of modeling the regression tree. If a tree has excessive nodes, in order to avoid the increasing complexity of the tree, the pre-pruning technology can be used to prune the potentially over-fitting branches. Model tree is binary tree. During each division only the best segmentation is selected. The application of pre-pruning technology is proposed in the Fourier model regression tree. In the “chooseBestSplit()” function of the program, we carry out an early condition-termination and then pre-pruning treatment is going.
2.5. Segmentation Step
The returned statistics of each category is counted for each feature;
The data set is cut into two categories;
Calculating the segmentation error, which is referred to the returned error of SEER in this paper;
If the error is less than the minimum error, then the current segmentation is set as the best segmentation and update the minimum error;
Return threshold and feature of the best segmentation.
3. The Analysis of the Experiment Results
Firstly implement the pretreatment of the imaginary parts, temporarily taking the first one thousand data and corresponding impulse response time via the solution of Fourier series model tree [7] , as shown in Figure 1.
{'spInd': 0, 'spVal': matrix([[448.]]);
'right': [matrix([[-3.11553926e-05]]), matrix([[-6.23107546e-05]]), matrix([[-0.00571539]])];
'left': [matrix([[0.00035834]]), matrix([[0.00071669]]), matrix([[0.03624532]])]}.
Above are partitioning points of the segmented Fourier series and the corresponding coefficients of the two Fourier series. The Fourier series to be fitted divided into two sections by model tree. The separation point corresponding to impulse response time indicates 448. Fourier series to the right of separation point is:
![]() (5)
(5)
Fourier series to the left of separation point is:
![]() (6)
(6)
Compare the fitting data acquired by the Fourier model tree with imaginary data of the actual impulse response, resulting the following diagram.
In Figure 5, the red line represents the first part of fitted data, the cyan line represents the second part of fitted data, the blue line represents the actually sampled imaginary data. The fitting effect is not particularly good, but it is quite more reliable compared with the linear fitting.
Similarly, Fourier series coefficients of the real parts impulse response are calculated by the model tree.
[matrix([[-9.09316919e-05]]), matrix([[-0.00018186]]), matrix([[ 0.03580918]])]
Because errors of characteristic components do not exceed errors SEER which resulted from branching, new branches don’t appear. The entire Fourier series is:
![]() (7)
(7)
In Figure 6, the red line represents the fitted data, the blue line represents the actually sampled real-part data. The fitting effect is reliable.
Then consider the prediction of the actually measured data, the one thousand data will be used as training data. And the rest of data will be used as test data for forecasting and analysis.
Obtain the fitting Fourier series of the one hundred and eighty thousand impulse response data of the imaginary parts, and draw the comparison chart as the following diagram.
![]()
Figure 5. Comparison of fitting data and imaginary parts data of the actual impulse response is solved by the Fourier series model tree.
![]()
Figure 6. Comparison of fitting data and real parts data of the actual collection.
In Figure 7, the red line represents the fitted data, and the blue line represents the actually measured data. Except for the sudden contour of edge cannot be portrayed in detail. The overall trend can be fitted effectively with the Fourier series. Due to the inadequacy of the terms of Fourier series, the overall trend can’t be described in detail. But this reduces the complexity of algorithm. On balance, select a lower frequency and make general fitting prediction.
The deviation rate is calculated according to formula of variance.
![]() (8)
(8)
The deviation rate between the fitted data and the real data of the imaginary parts is Devimg = 0.0698.
The comparison of one hundred and eighty thousand actually measured impulse response of the real parts is as the following diagram.
In Figure 8, the red line represents the fitted data, and the blue line represents the actually measured data. The
![]()
Figure 7. Comparison of actually measured data and fitting data of imaginary parts.
![]()
Figure 8. Comparison of fitting data and real data of real parts.
effect is good. The main part of the actually measured data can be calculated effectively.
The deviation rate of fitting data and real data of real parts is Devreal = 0.0675.
4. The Complexity of the Algorithm
The Fourier series model tree method is proposed through a lot of optimization in this paper. The platform is developed in Python. Its efficiency is greatly better than MATLAB [8] . The main advantages of performance lie in:
1) Search of two bifurcation tree is used in the model tree. The individual complexity of search is nlog(n), the branch is only two;
2) The calculation of Fourier series coefficients in the basis function does not use FFT transform, but through the establishment of coefficient equations. Gauss elimination method of numerical analysis is applied. Its complexity only depends on the number of iterations. The high number of cycles is two in the iterative operation, the complexity is n2.
To sum up, the total complexity of algorithm can make n3log(n) by multiplying computation complexity of basis function coefficient and the complexity of tree search.
5. Conclusion
The actually measured data by the Fourier series fitting are more reliable. Method of tree structure to achieve the segmented Fourier series can reduce the requirements of Fourier series order. After using the piecewise function, Fourier series can reduce order without sacrificing accuracy at the same time. Model tree of Fourier series will have the phenomenon of excessive segmentation in rare cases.
NOTES
*Author’s brief introduction: Huan Liu (1987- ), female, Harbin in Heilongjiang Province, a master’s degree, Information Engineering Institute of Southwest University of Science and Technology, Research orientation is algorithm. Hanlin Chen (1965- ), male, Sichuan Province, professor.