Boundary Value Problems for Burgers Equations, through Nonstandard Analysis ()
1. Introduction
The nonlinear parabolic partial differential equation
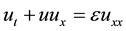 (1.1)
(1.1)
was first introduced by J. M. Burgers [1] [2] as the simplest model for fluid flow, this equation combining both nonlinear propagation effects and diffusive effect. If ε is not null, we approach to the Naveir’s Stokes equations in one dimension. Burgers equation has a wide variety of applications in the modeling of water in unsaturated soil, dynamics of soil water, statistics of flow problems mixing and turbulent diffusion cosmology and seismology.
When ε is null, this equation approaches to the Euler’s equations in one dimension who governs the flows of perfect fluids. It’s the viscid equation. it has the form
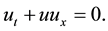 (1.2)
(1.2)
If the viscous term is dropped from the Burgers equation, discontinuities may appear in finite time; even if the initial condition is smooth, they give rise to the phenomenon of shock waves with important application in physics [3] . This property makes Burgers equation a proper model for testing numerical algorithms in flows where severe gradients or shocks are anticipated [4] -[6] . Discretization methods are well-known techniques for solving Burgers equation. Ascher and McLachlan established many methods as multi-symplectic box sheme. For the boundary value problem, Sinai [7] was interested to the initial condition case: null on  and Brownian on
and Brownian on . She, Aurell and Frich [8] with numerical calculations particularly examined the initial conditions of Brownian fraction nair to the asymptotic behavior.
. She, Aurell and Frich [8] with numerical calculations particularly examined the initial conditions of Brownian fraction nair to the asymptotic behavior.
A remarkable feature of viscid Burgers equation is that its solutions with initial conditions of the form
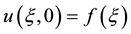 (1.3)
(1.3)
can be explicitly written down. Hopf [9] and Cole [10] independently showed that the Equation (1.1) can be linearized through the transformation
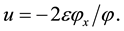 (1.4)
(1.4)
Then Hopf [9] showed that if  satisfies the linear heat equation
satisfies the linear heat equation
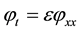 (1.5)
(1.5)
with initial condition
 (1.6)
(1.6)
Then 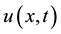 defined by Equation (1.4) solves (1.1) and (1.3). Conversely, if
defined by Equation (1.4) solves (1.1) and (1.3). Conversely, if  is a solution of problem (1.1) and (1.3) then
is a solution of problem (1.1) and (1.3) then  defined by Equation (1.4) is a solution of problem (1.5) and (1.6). Solving for
defined by Equation (1.4) is a solution of problem (1.5) and (1.6). Solving for 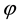 from (1.5) and (1.6) and substituting it into Equation (1.3) we obtained explicit formula for the solution of problem (1.1) and (1.2) namely:
from (1.5) and (1.6) and substituting it into Equation (1.3) we obtained explicit formula for the solution of problem (1.1) and (1.2) namely:
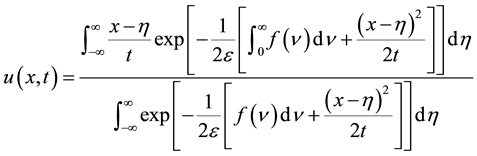 (1.7)
(1.7)
and studied the asymptotic behavior of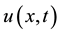 .
.
Explicit solutions of the Burgers equation (1.1) in the quarter plane with integrable initial data and piecewise constant boundary data were constructed by [11] using Hopf-Cole transformation [9] . He obtained a formula for its weak limit as viscosity parameter goes to 0. Although, there are many results for initial value problem has been studied less. Using maximum principle, this formula for weak limit was extended to general boundary data. ε is a positive parameter small enough. The problem is considered by [12] . As the fact that ε multiplies the largest derivative, one is in the presence of a singular perturbation problem. The purpose of Singular Perturbation Theory is to investigate the behavior of solutions of (1.1) as ![]()
The aim of the present article is to study solutions of Inviscid and Viscid Burgers equation if the initial condition admits several singular points, i.e. in the case of a finite number of shocks. A simple formulation is given for the asymptotic behavior based on the evaluation of integrals which is a method of the non standard perturbation theory of differential equations proposed by Imm Van Den Berg [13] and improved by Lutz and Callot.
Historically the subject non standard was developed by Robinson, Reeb, Lutz and Goze [14] . The nonstan- dard perturbation theory of differential equations, which is today a well-established tool in asymptotic theory, has its roots in the seventies, when the Reebian school (see [14] [15] ) introduced the use of nonstandard analysis into the field of perturbed differential equations. Our goal in this paper is to generalize these techniques on EDP and our general purpose is to describe the asymptotic behavior of solutions in boundary value problem with a small parameter ε and to discuss in particular the cases of confluence and the interacting shocks with new technical infinitesimal of non-standard analysis. We can conclude that the solutions of the problem: (1.1) and (1.3) are infinitely close to the solutions of problems (1.2) and (1.3), as ![]() is a parameter positive sufficiently small.
is a parameter positive sufficiently small.
In Section 2, we treat the boundary value problem for inviscid Burgers equation, solve it and study it. Section 3 is devoted to useful lemmas for our main results. In Section 4, we study viscid Burgers equation, solve exactly the initial value problems for it, and describe the asymptotic behavior of solutions with a non standard form. Some components, such as multi-leveled equations, graphics, and tables are not prescribed, although the various table text styles are provided. The formatter will need to create these components, incorporating the applicable criteria that follow.
2. Initial Boundary Value Problem for Inviscid Burgers’ Equation
2.1. Shock Fitting
We consider the inviscid Burgers equation:
![]()
In:![]() ,
, ![]() with the initial condition
with the initial condition
![]()
where ![]() is continuous.
is continuous.
This problem not admits the regular solutions but some weak solutions with certain regularity exist. The Burgers equation on the whole line is known to possess traveling wave solutions. The solution of (1.2) and (1.3) may be given in a parametric form and shocks must be fitted in such that:
![]() (2.1)
(2.1)
where ![]() and
and ![]() are the value of
are the value of ![]() on the two sides of the shock [16] .
on the two sides of the shock [16] .
According to Equation (1.2), the solution at time t is obtained from the initial profile ![]() by translating each point a distance
by translating each point a distance ![]() to the right. The shock cuts out the part corresponding to
to the right. The shock cuts out the part corresponding to![]() . If the discontinuity line, it is a straight line chord property still holds. The cord on the f curve cuts off lobes of equal area. The shock determination can then be describe entirely on the fixe
. If the discontinuity line, it is a straight line chord property still holds. The cord on the f curve cuts off lobes of equal area. The shock determination can then be describe entirely on the fixe ![]() curve by drawing all the chords with the equal area property can be written analytically as between the points
curve by drawing all the chords with the equal area property can be written analytically as between the points ![]() and
and ![]() on the curve
on the curve![]() . Moreover since areas are preserved under the mapping, the equal area
. Moreover since areas are preserved under the mapping, the equal area
![]() (2.2)
(2.2)
This is the differential equation for the line cord of shock that checks the condition of entropy such as [16] [17] Corresponding to the two inflection points.
2.2. Confluence of Shocks
When a number of shocks are produced, in general it is possible for one of them to overtake the shock ahead. Then they combine and continue as a single shock. This is also described by our shock solution.
Consider the curve given by f Figure 1, then two shocks are formed corresponding to the inflection points p and q with families of equal area chords, typified by ![]() and
and![]() .
.
As time goes, the points ![]() and
and ![]() approach each other until the stage in Figure 2 is reached where a common chord cuts off lobes of equal area for both humps.
approach each other until the stage in Figure 2 is reached where a common chord cuts off lobes of equal area for both humps.
At this stage the characteristics corresponding to ![]() and
and ![]() are the same and therefore the shocks have just combined into one as shown in Figure 3. Characteristics
are the same and therefore the shocks have just combined into one as shown in Figure 3. Characteristics ![]() and
and ![]() combined. All the characteristics between
combined. All the characteristics between ![]() and
and ![]() have now been absorbed by one or other of the shocks. A single shock proceeds using chords
have now been absorbed by one or other of the shocks. A single shock proceeds using chords![]() .
.
In the plane ![]() the shocks can be represented by Figure 4.
the shocks can be represented by Figure 4.
![]()
Figure 1. Graphic representation of the initial condition f.
![]()
Figure 2. Graphical representation from the merger of the two shocks. The characteristics ![]() and
and ![]() merge.
merge.
![]()
Figure 3. Construction for merging shocks in a final stage.
![]()
Figure 4. The (x, t) diagram for merging shocks corresponding to Figure 1.
3. Preliminaries
In this section we present some lemmas that are important to prove our main result.
Proposition 3.1. Let ![]() be the analytic solution for the initial value problem for the heat equation (1.5) and (1.6). If the initial condition is given as in Figure 1, then u given by the Formula (1.4) is a solution for the initial value problem (1.1) and (1.3). It is explicitly given by:
be the analytic solution for the initial value problem for the heat equation (1.5) and (1.6). If the initial condition is given as in Figure 1, then u given by the Formula (1.4) is a solution for the initial value problem (1.1) and (1.3). It is explicitly given by:
![]() (3.1)
(3.1)
i.e.
![]() (3.2)
(3.2)
Proof: When a shock overtakes another shock, they merge into a single shock of increased strength as described in inviscid solution![]() , on the f curve in Figure 1; It is possible to give a simple solution of Burgers equation that describes this process for arbitrary
, on the f curve in Figure 1; It is possible to give a simple solution of Burgers equation that describes this process for arbitrary![]() . The solution for a single shock is given in [3] [4] and the corresponding expression for
. The solution for a single shock is given in [3] [4] and the corresponding expression for ![]() may be written in the form:
may be written in the form:
![]() (3.3)
(3.3)
In the expression of solution for a single shock given in [3] [4] , the parameters b₁, b₂ witch locate the initial position of the shock are taken to be zero. The expressions ![]() are clearly solutions of the heat equation
are clearly solutions of the heat equation ![]() with
with
![]() (3.4)
(3.4)
Corresponding to the initial conditions:
![]() (3.5)
(3.5)
Then the solutions of the heat equation are given as:
![]() (3.6)
(3.6)
![]() (3.7)
(3.7)
Using Equations (1.4) and (3.1) we obtain the expression (3.2).
And to prove our results, we use the non standard analysis techniques, for that we consider the following lemma.
Lemma 3.2. (The Van. Den. Berg lemma [14] ): Let h be a standard function, defined and increasing on [0,+∞[ such that ![]() where δ for v ≃ 0.
where δ for v ≃ 0.![]() . And let
. And let ![]() be an intern function de-
be an intern function de-
fined on ]0,+∞[ such that :![]() for v ≈ 0, and such that ∀ d > 0, ∃ standard k and standard c
for v ≈ 0, and such that ∀ d > 0, ∃ standard k and standard c
such that:![]() , for
, for![]() . Then
. Then
![]() (3.8)
(3.8)
where a, r are positive standard, m and q are the both positive ![]() is an infinitesimal. b and s are standard,
is an infinitesimal. b and s are standard, ![]() and
and![]() .
.
To give estimation to the solution, given by (3.2), we state the following lemma:
Lemma 3.3. Let ε be a positive real small enough. And let ϕ and h be two standard functions such that: h, is a C2 class function verified the Lemma 3, and admits on the ξ point a unique absolute minimum ![]() and
and![]() .
.![]() . It is S-continuous on ξ and satisfies the conditions of the Lemma 3 in the both ways. Then
. It is S-continuous on ξ and satisfies the conditions of the Lemma 3 in the both ways. Then
![]() (3.9)
(3.9)
δ is an infinitesimal.
Proof: To prove this lemma, we use the “Van Den Berg” method, lemmas: (5.6), (5.7) [14] . It consists in the following steps
1) Search for the absolute minimum (maximum) of the function under the exponential sign and bring it out.
2) Bring back the minimum (maximum) to the zero.
3) Searching the galaxy as well as the main galaxy where the function in the exponential sign is appreciable.
4) Calculate the integral.
As consequence we have the following lemma.
Lemma 3.4. Let f the initial condition as Figure 1. Assume:
(H1): ![]() is C2(R).
is C2(R).
(H2): There exist a, b, c, d and e in R, with a < b < c < d < e, such that
![]()
Then for x and t fixed, the functions defined as:
![]() (3.10)
(3.10)
has at most two minima ![]() and
and ![]() relative to the variable
relative to the variable![]() . These two minima satisfy the equations:
. These two minima satisfy the equations:
![]() (3.11)
(3.11)
And the condition: ![]() is equivalent to the shock conditions:
is equivalent to the shock conditions:
![]() (3.12)
(3.12)
Proof: Let f the initial condition given as in Figure 1, two shocks are formed corresponding to the inflection points of![]() . for some time we see appear an area of three values for the solution
. for some time we see appear an area of three values for the solution![]() . At first the wave breaks on the feature for which:
. At first the wave breaks on the feature for which: ![]() and
and ![]() is a maximum during the time
is a maximum during the time![]() . Inside the zone of each shock and for a point
. Inside the zone of each shock and for a point![]() , there are three characteristics corresponding to two minimum framing a maximum. When a shock overtakes another, they merge into a single shock of increased strength as describe for the inviscid solution
, there are three characteristics corresponding to two minimum framing a maximum. When a shock overtakes another, they merge into a single shock of increased strength as describe for the inviscid solution ![]() on the f curve in Figure 2. The characteristics between
on the f curve in Figure 2. The characteristics between ![]() and
and ![]() are absorbed by one Figure 3. At this stage there are two stationary values that satisfy the equations (3.11) we noted them by
are absorbed by one Figure 3. At this stage there are two stationary values that satisfy the equations (3.11) we noted them by ![]() and
and![]() , each couple frames a maximum. Let:
, each couple frames a maximum. Let:![]() , be the minimum for the functions given by the Formula (3.10), is such that:
, be the minimum for the functions given by the Formula (3.10), is such that:
![]()
This equation is verified at the two minima ![]() and
and![]() . If
. If ![]() and within (3.10) this condition can be written as:
and within (3.10) this condition can be written as:
![]() (3.13)
(3.13)
But ![]() and
and ![]() both verify the equations:
both verify the equations:
![]() (3.14)
(3.14)
The condition of the shock is expressed by (3.12), is the same condition of shock given by (2.2) for invicid Burgers equation.
4. Initial Boundary Value Problem for Inviscid Burgers’ Equation
4.1. Confluence of Shocks
Our general purpose now is to show that the exact solution of (1.1) and (1.3) endorse the ideas regarding shocks in Section 2, we want to confirm that as ![]() is small enough, the solution of (1.1) and (1.3) reduce to solution of (1.2) and (1.3), with discontinuous shocks which satisfy the condition (2.2), and the shocks are located at the positions determined in Section 2. The shocks are formed corresponding to the inflection points of the initial condition
is small enough, the solution of (1.1) and (1.3) reduce to solution of (1.2) and (1.3), with discontinuous shocks which satisfy the condition (2.2), and the shocks are located at the positions determined in Section 2. The shocks are formed corresponding to the inflection points of the initial condition![]() , who assume the assumptions (H1), (H2) in the lemma (3.4). Then we proved the following result:
, who assume the assumptions (H1), (H2) in the lemma (3.4). Then we proved the following result:
Theorem 4.1. Under the assumptions: (H1), (H2) in lemma (3.4), the problem (1.1) and (1.3) admits a unique solution for ![]() given by:
given by:
![]() (4.1)
(4.1)
Such a solution is confluence of shocks and for ε sufficiently small, this solution is infinitely close to the solution of the reduced problem given in (2.2).
Proof: 1) From Figure 2 and Figure 3, after some time the two shocks combine and continue into one, and this is the lowest minimum that carries this amount to the case of a single shock. From the proposition (3.1), the problem (1.1) and (1.3) admits a single solution explicitly given by Formula (4.1). Uniqueness is due to the condition of entropy which restricts the set of solutions to one which is stable with a singular perturbation dissipative nature.
2) Let ![]() be a standard point outside the line of the shock. From the solutions of the equation
be a standard point outside the line of the shock. From the solutions of the equation ![]() , there is only one denoted
, there is only one denoted ![]() is the absolute minimum of the function given by the expression (3.10). Using the expressions (3.1) and (3.2) of the Proposition 3.1
is the absolute minimum of the function given by the expression (3.10). Using the expressions (3.1) and (3.2) of the Proposition 3.1 ![]() is given as:
is given as:
![]()
From the Lemma 3.2 we have
![]()
where δ > 0 is an infinitesimal. And we will have the following estimate
![]()
To conclude we have the following corollary.
Corollary 4.2. Let![]() , be a standard point outside each line of shock. Among the solutions of the equation
, be a standard point outside each line of shock. Among the solutions of the equation![]() , one denoted
, one denoted ![]() is the absolute minimum of the function
is the absolute minimum of the function ![]() given by (3.10), and further the solution of (1.1) and (1.3) verifies at the point
given by (3.10), and further the solution of (1.1) and (1.3) verifies at the point ![]()
![]()
![]()
And the center of the shock when ![]() is that:
is that:
![]()
Proof: Using lemma (3.4), outside the region of each shock. For ![]() fixed, each function
fixed, each function ![]() has an absolute minimum at
has an absolute minimum at![]() . In (3.1)
. In (3.1) ![]() is in the form
is in the form
![]()
With ![]() and
and ![]() are given by (3.6) and (3.7). Then
are given by (3.6) and (3.7). Then
![]()
Using lemma (3.3) we obtain
![]()
And it follows that:
If![]() ,
, ![]() function dominates when x is infinitely large positive and there is obtained
function dominates when x is infinitely large positive and there is obtained
![]()
If![]() ,
, ![]() function dominates when x is infinitely large negative and there is obtained
function dominates when x is infinitely large negative and there is obtained
![]()
4.2. Interacting Shocks
In this section, we discuss the interacting shocks case; before going further in this case we need the following proposition and lemma.
Now since any ![]() a solution of the heat equation, we may clearly add further terms in (3.3) and generate more general solution of burgers’ equation. Such solution represents interacting shocks. As consequence we have the following
a solution of the heat equation, we may clearly add further terms in (3.3) and generate more general solution of burgers’ equation. Such solution represents interacting shocks. As consequence we have the following
Proposition 4.3. Let![]() , be the analytical solution for the problem (1.5) and (1.3). If f is the initial condition admitting three inflection points, then the solution of (1.1) and (1.3) is explicitly given by
, be the analytical solution for the problem (1.5) and (1.3). If f is the initial condition admitting three inflection points, then the solution of (1.1) and (1.3) is explicitly given by
![]() (4.2)
(4.2)
i.e.
![]() (4.3)
(4.3)
Proof: When a shock overtakes another, they merge into a single shock of increased strength as described in inviscid solution![]() . For arbitrary
. For arbitrary![]() , it is possible to provide a simple solution to the Burgers equation that describes this process. The solution for a single shock is given in [4] and the corresponding expression for
, it is possible to provide a simple solution to the Burgers equation that describes this process. The solution for a single shock is given in [4] and the corresponding expression for ![]() is written as:
is written as:
![]()
In the solution for a single shock given in [4] , the parameters ![]() which locate the initial position of the
which locate the initial position of the
shock are taken to be zero and![]() . The expressions
. The expressions![]() ,
, ![]() and
and ![]() are clearly solution of the
are clearly solution of the
heat equation ![]() with
with
![]() (4.5)
(4.5)
And
![]() (4.6)
(4.6)
Corresponding to the initial conditions:
![]() (4.7)
(4.7)
Then the solutions of the heat equation are given as:
![]() (4.8)
(4.8)
and
![]() (4.9)
(4.9)
Using (1.4) and (4.4) we obtain the expression (4.3). Then we have the following.
Theorem 4.4. For![]() , and for
, and for![]() , the problems (1.1) and (1.3) have a unique solution given by:
, the problems (1.1) and (1.3) have a unique solution given by:
![]()
Such a solution is interacting shocks and for ε sufficiently small, it is infinitely close to the solution of the reduced problems (1.2) and (1.3).
Proof. 1) In the interacting shock case we have three shocks, when a shock overtakes another they merge into a single shock of increased strength and the lowest minimum dominating. Then we go back to the single shock case. Using the proposition (4.3), we deduce the uniqueness of solution explicitly given by (3.4). The uniqueness is due to the entropic condition [3] [4] , which restricts the set of solutions to one, who is stable with singular perturbation with dissipative nature.
2) Let ![]() be a standard point outside the line of the shock. From the solutions of the equation
be a standard point outside the line of the shock. From the solutions of the equation ![]() , there is only one denoted that
, there is only one denoted that ![]() is the absolute minimum of the function given by the expression (3.10).
is the absolute minimum of the function given by the expression (3.10). ![]() is given as
is given as
![]()
From the Lemma 3.2 we have:
![]()
where δ > 0 is an infinitesimal. And we will have the following estimate
![]()
from which the following corollary
Corollary 4.5. Let ![]() be a standard point outside the line of the shock. So there exists a unique solution denoted
be a standard point outside the line of the shock. So there exists a unique solution denoted ![]() which is the absolute minimum of the function given by (3.10). If
which is the absolute minimum of the function given by (3.10). If ![]() is reasonably small, we can recognise shock transition between the states
is reasonably small, we can recognise shock transition between the states ![]() by noting in which regions the corresponding
by noting in which regions the corresponding ![]() dominates. At
dominates. At![]() ,
, ![]() dominates in
dominates in![]() ,
, ![]() in:
in:![]() ;
; ![]() dominates in:
dominates in:![]() . Then
. Then
![]()
![]()
![]()
Proof: For ![]() fixed, outside the shock region and by the use of the lemma (3.2), each function
fixed, outside the shock region and by the use of the lemma (3.2), each function ![]() admits one absolute minimum on the point
admits one absolute minimum on the point![]() . In Formula (3.4),
. In Formula (3.4), ![]() is as
is as
![]() (4.11)
(4.11)
where ![]() are given by (4.8) and (4.9); and using the Lemma 3.2 there are equivalent to those
are given by (4.8) and (4.9); and using the Lemma 3.2 there are equivalent to those
![]() (4.12)
(4.12)
![]() (4.13)
(4.13)
where δ is an infinitesimal positive real.
As shown in Figure 5, If ![]() is reasonably small, we can recognise shock transition between the states
is reasonably small, we can recognise shock transition between the states ![]() by noting in which regions the corresponding
by noting in which regions the corresponding ![]() dominates. At
dominates. At![]() , in:
, in:![]() ,
, ![]() dominates and we have:
dominates and we have:
![]()
![]() dominates in:
dominates in:![]() , then we have:
, then we have:
![]()
In:![]() ,
, ![]() dominates and we obtain:
dominates and we obtain:
![]()
The symbol “≃” means infinitely close to [8] . Thus we have a shock transitions from ![]() to
to ![]() centred at
centred at![]() , and one from
, and one from ![]() to
to ![]() centered at
centered at![]() . For
. For![]() , for early times the transition from
, for early times the transition from ![]() to
to ![]() occurs where
occurs where ![]() on
on
![]() (4.14)
(4.14)
The transition from ![]() to
to ![]() occurs where
occurs where ![]() on
on
![]() (4.15)
(4.15)
Since, ![]() , the second shock overtakes the first at the point
, the second shock overtakes the first at the point ![]() determined by (4.14) and (4.15). At this point
determined by (4.14) and (4.15). At this point
![]()
for![]() , there is no longer any region where
, there is no longer any region where ![]() dominates and the continuing solution describe a single shock transition between u1 and u3, moving with the velocity
dominates and the continuing solution describe a single shock transition between u1 and u3, moving with the velocity
![]()
on the path determined by ![]()
Acknowledgements
I thank the editor and the referee for their comments.