Compressive Sensing Algorithms for Signal Processing Applications: A Survey ()
1. Introduction
The traditional approach of reconstructing signals or images from measured data follows the well-known Shannon sampling theorem, which states that the sampling rate must be twice the highest frequency. Similarly, the fundamental theorem of linear algebra suggests that the number of collected samples (measurements) of a discrete finite-dimensional signal should be at least as large as its length (its dimension) in order to ensure reconstruction. This principle underlies most devices of current technology, such as analog to digital conversion and medical imaging. The novel theory of compressive sensing provides a fundamentally new approach to data acquisition which overcomes this common wisdom. It predicts that certain signals or images can be recovered from what was previously believed to be highly incomplete measurements (information).
The efficiency of many lossy compression techniques, such as JPEG and MP3, relies on the empirical obser- vation that many types of signals can be well-approximated by only a small number of non-zero coefficients. A compression is obtained by simply storing only the largest basis coefficients and the non-stored coefficients are simply set to zero. This is certainly a reasonable strategy when full information of the signal is available. However, when the signal first has to be acquired by a somewhat costly, lengthy or otherwise difficult measurement procedure, this seems to be a waste of resources: Thus, large efforts are spent in order to obtain full information on the signal, and afterwards most of the information is thrown away at the compression stage. In CS based techniques, a clever way is adopted for obtaining the compressed version of the signal directly, by taking only a small number of measurements of the signal. It is not obvious at all whether this is possible since measuring directly the large coefficients requires knowing a priori their location. In fact, compressive sensing provides a way of reconstructing a compressed version of the original signal by taking only a small amount of linear and non- adaptive measurements. The precise number of required measurements is comparable to the compressed size of the signal. In many cases, the measurements are suitably designed through the use of random matrices. It is for this reason that the theory of compressive sensing uses a lot of tools from probability theory.
It is another important feature of compressive sensing that practical reconstruction can be performed by using efficient algorithms. Since the interest is in the vastly under-sampled case, the linear system describing the measurements is underdetermined and therefore has infinitely many solutions. The key idea is that the sparsity helps in isolating the original vector. The first naive approach to a reconstruction algorithm consists in searching for the sparsest vector that is consistent with the linear measurements. This leads to the combinatorial 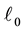 -pro- blem, which unfortunately is Non-deterministic Polynomial-time hard (NP-hard) in general. More precisely, a problem H is NP-hard when every problem L in NP can be reduced in polynomial time to H.
-pro- blem, which unfortunately is Non-deterministic Polynomial-time hard (NP-hard) in general. More precisely, a problem H is NP-hard when every problem L in NP can be reduced in polynomial time to H.
There are essentially two approaches for tractable alternative algorithms. The first is convex relaxation lead- ing to 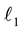 -minimization―also known as basis pursuit, while the second constructs greedy algorithms. By now basic properties of the measurement matrix which ensure sparse recovery by
-minimization―also known as basis pursuit, while the second constructs greedy algorithms. By now basic properties of the measurement matrix which ensure sparse recovery by  -minimization are known: the Null Space Property (NSP) and the Restricted Isometry Property (RIP). The later requires that all column sub- matrices of a certain size of the measurement matrix are well-conditioned. This is where probabilistic methods come into play because it is quite hard to analyze these properties for deterministic matrices with minimal amount of measurements. Among the provably good measurement matrices are Gaussian, Bernoulli random matrices, and partial random Fourier matrices.
-minimization are known: the Null Space Property (NSP) and the Restricted Isometry Property (RIP). The later requires that all column sub- matrices of a certain size of the measurement matrix are well-conditioned. This is where probabilistic methods come into play because it is quite hard to analyze these properties for deterministic matrices with minimal amount of measurements. Among the provably good measurement matrices are Gaussian, Bernoulli random matrices, and partial random Fourier matrices.
To illustrate the above idea, we consider the 300 samples length time-domain signal 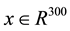 shown in Figure 1(a) that represents 10 different sinusoids as shown in Figure 1(b). From Figure 1(b), it is clear that the signal is sparse in frequency domain since only 10 non-zero values exist among the 300 frequencies. Considering only 30 samples (indicated by the red dots in Figure 1(a)) and adopting a suitable recovery process (e.g.
shown in Figure 1(a) that represents 10 different sinusoids as shown in Figure 1(b). From Figure 1(b), it is clear that the signal is sparse in frequency domain since only 10 non-zero values exist among the 300 frequencies. Considering only 30 samples (indicated by the red dots in Figure 1(a)) and adopting a suitable recovery process (e.g. 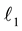 - minimization), the signal is exact reconstruction with no recovery error at all as shown in Figure 1(c).
- minimization), the signal is exact reconstruction with no recovery error at all as shown in Figure 1(c).
This paper gives a literature review of both theoretical and numerical aspects of compressive sensing. This section introduces the CS principals and concepts. The rest of this paper is organized as follows. The notations and concepts including vector spaces, basic notations, the Restricted Isometry Property (RIP) and coherence property
are introduced in Section 2. Sections 3 and 4 present CS motivations and fundamentals respectively. In Section 5, sparse representations including time-domain representation, discrete Fourier, discrete cosine and discrete wavelet transformations are presented. Section 6 presents some signal reconstruction algorithms. Section 7 gives some highlighted results in terms of random sensing matrices, deterministic sensing matrices and their drawbacks. Sections 8 and 9 present some practical CS applications and three illustrative numerical examples respectively. Finally Section 10 gives the main information sources.
2. Preliminaries, Notations and Concepts
For clarity of presentation, it will be convenient to introduce some notations and concepts that we will use throughout the remainder of the paper.
2.1. Vector Spaces and Basic Notation
For much of its history, signal processing has focused on signals produced by physical systems. Many natural and man-made systems can be modeled as linear. Thus, it is natural to consider signal models that complement this kind of linear structure. This notion has been incorporated into modern signal processing by modeling signals as vectors living in an appropriate vector space. This captures the linear structure that we often desire, namely that if we add two signals together then we obtain a new, physically meaningful signal. Moreover, vector spaces allow us to apply intuitions and tools from geometry in R3, such as lengths, and angles, to describe and compare signals of interest.
Throughout this paper, we will treat signals as real valued functions having domains that are either continuous or discrete, and either infinite or finite. In the following only a brief review of some of the key concepts in vector spaces that will be required in developing the theory of compressive sensing will be considered [1] . We will typically be concerned with normed vector spaces, i.e., vector spaces endowed with a norm. In the case of a discrete, finite domain, we can view the signals as vectors in an N-dimensional Euclidean space, denoted by . When dealing with vectors in
. When dealing with vectors in , we will make frequent use of the
, we will make frequent use of the ![]() norms, which are defined for
norms, which are defined for
![]() as
as
![]() (1)
(1)
In Euclidean space we can also consider the standard inner product in![]() , which we denote
, which we denote
![]() (2)
(2)
This inner product leads to the ![]() norm:
norm:![]() . In some contexts it is useful to extend the notion
. In some contexts it is useful to extend the notion
of ![]() norms to the case where
norms to the case where![]() . In this case, the norm defined in (1) fails to satisfy the triangle inequa-
. In this case, the norm defined in (1) fails to satisfy the triangle inequa-
lity, so it is actually a quasi-norm. We will also make frequent use of the notation![]() , where
, where ![]() denotes the support of
denotes the support of ![]() and
and ![]() denotes the cardinality of
denotes the cardinality of![]() . Note that
. Note that ![]() is not even a quasi-norm, but one can easily show that
is not even a quasi-norm, but one can easily show that
![]() (3)
(3)
justifying this choice of notation. The ![]() (quasi-) norms have notably different properties for different values
(quasi-) norms have notably different properties for different values
of![]() . To illustrate this, in Figure 2 we show the unit sphere, i.e.,
. To illustrate this, in Figure 2 we show the unit sphere, i.e.,![]() ; induced by each of these
; induced by each of these
norms in![]() . Note that for
. Note that for ![]() the corresponding unit sphere is non-convex (reflecting the quasi-norm’s violation of the triangle inequality). Typically norms are used as a measure of the strength of a signal, or the size of an error. For example, suppose we are given a signal
the corresponding unit sphere is non-convex (reflecting the quasi-norm’s violation of the triangle inequality). Typically norms are used as a measure of the strength of a signal, or the size of an error. For example, suppose we are given a signal ![]() and wish to approximate it using a point in a one- dimensional affine space A. If we measure the approximation error using an
and wish to approximate it using a point in a one- dimensional affine space A. If we measure the approximation error using an ![]() norm, then our task is to
norm, then our task is to
find the ![]() that minimizes
that minimizes![]() . The choice of
. The choice of ![]() will have a significant effect on the properties of
will have a significant effect on the properties of
the resulting approximation error as illustrated in Figure 3. To compute the closest point in A to ![]() using each
using each ![]() norm, we can imagine growing an
norm, we can imagine growing an ![]() sphere centered on
sphere centered on ![]() until it intersects with A. This will be the point
until it intersects with A. This will be the point ![]() that is closest to
that is closest to ![]() in the corresponding
in the corresponding ![]() norm. It should be noticed that larger
norm. It should be noticed that larger ![]() tends to spread out the error more evenly among the two coefficients, while smaller
tends to spread out the error more evenly among the two coefficients, while smaller ![]() leads to an error that is more unevenly distributed and tends to be sparse. This intuition plays an important role in the development of CS theory.
leads to an error that is more unevenly distributed and tends to be sparse. This intuition plays an important role in the development of CS theory.
2.2. The Restricted Isometry Property
In linear algebra, an orthogonal matrix is a square matrix with real entries whose columns and rows are orthogonal unit vectors (i.e., orthonormal vectors), i.e.![]() , where
, where ![]() is the identity matrix. This leads to the equivalent characterization: a matrix A is orthogonal if its transpose is equal to its inverse; i.e.,
is the identity matrix. This leads to the equivalent characterization: a matrix A is orthogonal if its transpose is equal to its inverse; i.e.,![]() . The determinant of any orthogonal matrix is either +1 or −1. As a linear transformation, an orthogonal matrix preserves the dot product of vectors, and therefore acts as an isometry of Euclidean space, such as a rotation or reflection.
. The determinant of any orthogonal matrix is either +1 or −1. As a linear transformation, an orthogonal matrix preserves the dot product of vectors, and therefore acts as an isometry of Euclidean space, such as a rotation or reflection.
The restricted isometry property characterizes matrices which are nearly orthonormal, at least when operating on sparse vectors. The concept was introduced by Emmanuel Candès and Terence Tao [2] and is used to prove many theorems in the field of compressed sensing. There are no known large matrices with bounded restricted isometry constants (and computing these constants is NP-hard), but many random matrices have been shown to remain bounded. In particular, it has been shown that with exponentially high probability, random Gaussian, Bernoulli, and partial Fourier matrices satisfy the RIP with number of measurements nearly linear in the sparsity level. The current smallest upper bounds for any large rectangular matrices are for those of Gaussian matrices. Let A be an ![]() matrix and let
matrix and let ![]() be an integer. Suppose that there exists a constant
be an integer. Suppose that there exists a constant ![]() such that, for every
such that, for every ![]() sub-matrix
sub-matrix ![]() of A and for every vector y,
of A and for every vector y,
![]() (4)
(4)
Then, the matrix A is said to satisfy the s-restricted isometry property with restricted isometry constant![]() .
.
2.3. The Concept of Coherence
The concept of coherence was introduced in a slightly less general framework in [3] , and has since been used extensively in the field of sparse representations of signals. In particular, it is used as a measure of the ability of suboptimal algorithms such as matching pursuit and basis pursuit to correctly identify the true representation of a sparse signal. Current assumptions in the field of compressed sensing and sparse signal recovery impose that the measurement matrix has uncorrelated columns. To be formal, one defines the coherence or the mutual coherence of a matrix A is defined as the maximum absolute value of the cross-correlations between the columns of A. Formally, let ![]() be the columns of the matrix A, which are assumed to be normalized such that
be the columns of the matrix A, which are assumed to be normalized such that![]() . The mutual coherence of A is then defined as
. The mutual coherence of A is then defined as
![]() (5)
(5)
A lower bound is
![]() (6)
(6)
We say that a dictionary is incoherent if ![]() is small. Standard results then require that the measurement matrix satisfy a strict incoherence property, as even the RIP imposes this. If the dictionary D is highly coherent, then the matrix AD will also be coherent in general.
is small. Standard results then require that the measurement matrix satisfy a strict incoherence property, as even the RIP imposes this. If the dictionary D is highly coherent, then the matrix AD will also be coherent in general.
Coherence is in some sense a natural property in the compressed sensing framework, for if two columns are closely correlated, it will be impossible in general to distinguish whether the energy in the signal comes from one or the other. For example, imagine that we are not under sampling and that A is the identity so that we observe![]() . Suppose the first two columns are identical,
. Suppose the first two columns are identical,![]() . Then the measurement
. Then the measurement ![]() can be explained by the input vectors
can be explained by the input vectors ![]() or
or ![]() or any convex combination. Thus there is no hope of reconstructing a unique sparse signal x from measurements
or any convex combination. Thus there is no hope of reconstructing a unique sparse signal x from measurements![]() . However, we are not interested in recovering the coeffi- cient vector x, but rather the actual signal
. However, we are not interested in recovering the coeffi- cient vector x, but rather the actual signal![]() .
.
3. Compressive Sensing Motivation
In the big data era, in order to control the cost, complexity, and bandwidth of collecting and processing high- dimensional data systems, it is critical to exploit models that encapsulate prior information regarding the signals of interest. Many N-samples signals can be well described by using only K-parameters, where K is much fewer than N. Indeed there exist a wide variety of techniques for data reduction using low dimensional models to re- duce the burden of processing. The field of compressive sensing has been motivated by the goal of reducing sensing costs, for general sensing missions. Examples include:
Data compression: reducing the number of bits required to store a high-dimensional signal while preserving its critical information.
Parameter estimation: discerning the specific values of the underlying degrees of freedom of a high-dimen- sional signal.
Feature extraction: extracting information carrying characteristics from a high-dimensional signal.
Channel estimation: Clearly the motivation to use compressive sensing in channel estimation is the observation that some channels are characterized by sparse multipath―by that we mean that there are much fewer distinct arrivals as there are baseband channel taps.
4. Compressive Sensing Fundamentals
In a traditional acquisition system, all samples of the original signal are acquired. This number of signal samples can be in the order of millions, as is the case for instance with digital images. The acquisition process is followed by compression, which takes advantage of the redundancy (or the structure) in the signal to represent it in a domain where most of the signal coefficients can be discarded with little or no loss in quality. For instance, for a typical image of a natural scene, an almost lossless approximation can be achieved with only about 5% of the frequency (e.g., wavelet, DCT) coefficients. Hence, traditional acquisition systems first acquire a huge amount of data, a significant portion of which is immediately discarded (compression). This creates an important inefficiency in many practical applications. Compressive sensing addresses this inefficiency by effectively combining the acquisition and compression processes. Traditional decoding is replaced by recovery algorithms that exploit the underlying structure of the data [4] .
CS has become a very active research area in recent years due to its interesting theoretical nature and its practical utility in a wide range of applications. Compressive sensing is a new approach to capture a wide range of signals at a rate significantly lower than the Nyquist rate. In the following we provide a brief overview of the basic principles of CS, since they will form the basis of most signal processing applications. The classical sampling theory pioneered by Nyquist, Whittaker and Shannon [5] relies on the assumption that the signals to be acquired are band-limited to a maximum frequency: the Nyquist frequency. Even if this hypothesis does not hold, the signals can simply be low-pass filtered before being sampled at a rate at least twice the Nyquist frequency. Compressed sensing is a revolutionary signal acquisition scheme that allows a signal to be acquired and accurately reconstructed with significantly fewer samples than required by Nyquist-rate sampling. Unlike Nyquist sampling, which relies on the maximum rate-of-change of a signal, compressed sensing relies on the maximum rate-of- information in a signal. Compressed sensing has been instrumental in research for low-power data acquisition methods.
CS theory states that a signal can be sampled without any information loss at a rate close to its information content. CS relies on two fundamental properties: signals parsity and incoherence [6] . Signals are represented with varying levels of sparsity indifferent domains. For example, a single tone sine wave is either represented by a single frequency coefficient or by an infinite number of time-domain samples. Consider a real-valued, finite- length, one-dimensional, discrete-time signal x, which we view as an ![]() column vector in
column vector in ![]() with elements
with elements![]() ,
,![]() . We treat an image or higher-dimensional data by vectorizing it into a long one-
. We treat an image or higher-dimensional data by vectorizing it into a long one-
dimensional vector. Any signal in ![]() can be represented in terms of a basis of
can be represented in terms of a basis of ![]() vectors
vectors![]() . For simplicity, assume that the basis is orthonormal. Forming the
. For simplicity, assume that the basis is orthonormal. Forming the ![]() basis matrix
basis matrix ![]() by
by
stacking the vectors ![]() as columns, we can express any signal x as
as columns, we can express any signal x as
![]() (7)
(7)
where ![]() is the
is the ![]() column vector of weighting coefficients
column vector of weighting coefficients ![]() and where
and where ![]() denotes the
denotes the
transpose operation. Clearly, x and s are equivalent representations of the same signal, with x in the time domain and s in the ![]() domain. We will focus on signals that have a sparse representation, where x is a linear combination of just K basis vectors, with
domain. We will focus on signals that have a sparse representation, where x is a linear combination of just K basis vectors, with![]() . That is, only K of the
. That is, only K of the ![]() in (7) are nonzero and
in (7) are nonzero and ![]() are zero. Sparsity is motivated by the fact that many natural and manmade signals are compressible in the sense that
are zero. Sparsity is motivated by the fact that many natural and manmade signals are compressible in the sense that
there exists a basis ![]() where the representation (7) has just a few large coefficients and many small
where the representation (7) has just a few large coefficients and many small
coefficients. Compressible signals are well approximated by K-sparse representations; this is the basis of transform coding. For example, natural images tend to be compressible in the discrete cosine and wavelet bases on which the JPEG and JPEG-2000 compression standards are based. Audio signals and many communication signals are compressible in a localized Fourier basis.
Transform coding plays a central role in data acquisition systems where the number of samples is high. In this framework, we acquire the full N-sample signal x; compute the complete set of transform coefficients ![]() via
via![]() ; locate the K largest coefficients and discard the
; locate the K largest coefficients and discard the ![]() smallest coefficients; and encode the K values and locations of the largest coefficients. Unfortunately, the sample-then-compress framework suffers from three inherent inefficiencies: First, we must start with a potentially large number of samples N even if the ulti- mate desired K is small. Second, the encoder must compute all of the N transform coefficients
smallest coefficients; and encode the K values and locations of the largest coefficients. Unfortunately, the sample-then-compress framework suffers from three inherent inefficiencies: First, we must start with a potentially large number of samples N even if the ulti- mate desired K is small. Second, the encoder must compute all of the N transform coefficients![]() , even though it will discard all but K of them. Third, the encoder faces the overhead of encoding the locations of the large coefficients. As an alternative, we will study a more general data acquisition approach that condenses the signal directly into a compressed representation without going through the intermediate stage of taking N samples. Consider the more general linear measurement process that computes
, even though it will discard all but K of them. Third, the encoder faces the overhead of encoding the locations of the large coefficients. As an alternative, we will study a more general data acquisition approach that condenses the signal directly into a compressed representation without going through the intermediate stage of taking N samples. Consider the more general linear measurement process that computes ![]() inner products between
inner products between ![]()
and a collection of vectors ![]() as in
as in![]() . Stacking the measurements
. Stacking the measurements ![]() into the
into the ![]() vector y and the measurement vectors
vector y and the measurement vectors ![]() as rows into an
as rows into an ![]() matrix
matrix ![]() and substituting in (7), we can
and substituting in (7), we can
write
![]() (8)
(8)
where ![]() is an
is an ![]() matrix. See Figure 4(a) for a pictorial depiction of (8). Note that the measurement process is non-adaptive; that is,
matrix. See Figure 4(a) for a pictorial depiction of (8). Note that the measurement process is non-adaptive; that is, ![]() does not depend in any way on the signal x. Here, the goal in the following is to design a measurement matrix
does not depend in any way on the signal x. Here, the goal in the following is to design a measurement matrix ![]() and a reconstruction algorithm for K-sparse and compressible signals that require only
and a reconstruction algorithm for K-sparse and compressible signals that require only ![]() or slightly more measurements, or about as many measurements as the number of coefficients encoded in a traditional transform coder. This approach is based on the theory of compressive sensing introduced in [3] - [7] . However, in this case the system is undetermined, which means there are an infinite number of solutions for x. However, the signal is known a-priori to be sparse. Under certain conditions, the sparsest signal representation satisfying Equation (8) can be shown to be unique. Software have explained the first component of compressed sensing; which is the signal sparsity. The next important property of compressed sensing is incoherent sampling. It measures the largest correlation between any two elements of
or slightly more measurements, or about as many measurements as the number of coefficients encoded in a traditional transform coder. This approach is based on the theory of compressive sensing introduced in [3] - [7] . However, in this case the system is undetermined, which means there are an infinite number of solutions for x. However, the signal is known a-priori to be sparse. Under certain conditions, the sparsest signal representation satisfying Equation (8) can be shown to be unique. Software have explained the first component of compressed sensing; which is the signal sparsity. The next important property of compressed sensing is incoherent sampling. It measures the largest correlation between any two elements of ![]() and
and ![]() (i.e., any row of
(i.e., any row of ![]() and column of
and column of![]() ), can be defined as:
), can be defined as:
![]() (9)
(9)
The coherence![]() , can range between 1 and
, can range between 1 and ![]() [5] . As it is shown in [2] , the minimum number of measurements needed to recover the signal with over whelming probability is as follow:
[5] . As it is shown in [2] , the minimum number of measurements needed to recover the signal with over whelming probability is as follow:
![]() (10)
(10)
where, C is appositive constant, K is the number of significant non-zero coefficients in x, and N is the dimension of the signal to be recovered. In other words, the less coherence between Φ and Ψ the fewer number of measurements needed to recover the signal. Hence, to minimize the required number of measurements, it is required to have the minimum coherence between ![]() and
and![]() . Random matrices are a good candidate for sampling matrix as they have low coherence with any fixed basis, and, as a result, the signal basis
. Random matrices are a good candidate for sampling matrix as they have low coherence with any fixed basis, and, as a result, the signal basis ![]() is not required to be known in advance in order to determine a suitable sampling matrix,
is not required to be known in advance in order to determine a suitable sampling matrix, ![]() [7] .
[7] .
5. Sparse Representations
Many natural signals are compressible by transforming them to some domain―e.g. Sounds are compactly re- presented in the frequency domain and images in the wavelet domain. But, compression is typically performed after the signal is completely acquired. Advances in compressive sensing suggest that if the signal is sparse or compressible, the sampling process can itself be designed so as to acquire only essential information. Transforming a signal to a new basis or frame may allow us to represent a signal more concisely. The resulting compression is useful for reducing data storage and data transmission, which can be quite expensive in some applications. Hence, one might wish to simply transmit the analysis coefficients obtained in the new basis or frame expansion instead of its high-dimensional correlate. In cases where the number of non-zero coefficients is small, we say that we have a sparse representation. Sparse signal models allow us to achieve high rates of compression and in the case of compressive sensing we may use the knowledge that the signal is sparse in a known basis or frame to recover the original signal from a small number of measurements. For sparse data, only the non-zero coefficients need to be stored or transmitted in many cases; the rest can be assumed to be zero. Mathematically, we say that a signal x is K-sparse when it has at most K non-zeros, i.e.,![]() . We let
. We let
![]() (11)
(11)
denotes the set of all K-sparse signals. Typically, we deal with signals that are not themselves sparse, but which admit a sparse representation in some basis![]() . In this case we will still refer to x as being K-sparse, with the
. In this case we will still refer to x as being K-sparse, with the
understanding that we can express x as ![]() where
where![]() .
.
Sparsity has long been exploited in signal processing and approximation theory for tasks such as compression [8] and denoising [9] . Sparsity also has been exploited heavily in image processing tasks, since the multi-scale wavelet transform [10] provides nearly sparse representations for natural images. As an example of one-dimen- sional (1-D) signal that has different signal sparisity consider the signal
![]()
where![]() . One can interpret sampling as a basis expansion where the elements in the basis are impulses placed at periodic points along the time axis. In this case, the dual basis consists of sinc functions used to reconstruct the signal from the discrete-time samples. This representation contains many non-zero coefficients, and due to the signal’s periodicity, there are many redundant measurements. Representing the signal in the Four- ier basis, on the other hand, requires only two non-zero basis vectors, scaled appropriately at the positive and negative frequencies. Applying the Discrete Cosine Transform (DCT) to the signal, shows that only 335 non- zero DCT coefficients represents the signal
. One can interpret sampling as a basis expansion where the elements in the basis are impulses placed at periodic points along the time axis. In this case, the dual basis consists of sinc functions used to reconstruct the signal from the discrete-time samples. This representation contains many non-zero coefficients, and due to the signal’s periodicity, there are many redundant measurements. Representing the signal in the Four- ier basis, on the other hand, requires only two non-zero basis vectors, scaled appropriately at the positive and negative frequencies. Applying the Discrete Cosine Transform (DCT) to the signal, shows that only 335 non- zero DCT coefficients represents the signal![]() . Similarly, applying the Discrete Wavelet Transform (DWT) to the signal shows that only 265 non-zero DWT coefficients represents the signal
. Similarly, applying the Discrete Wavelet Transform (DWT) to the signal shows that only 265 non-zero DWT coefficients represents the signal![]() . Figure 5 illustrates the four basis expansions that yield different levels of sparsity for the same signal
. Figure 5 illustrates the four basis expansions that yield different levels of sparsity for the same signal![]() .
.
An important assumption used in the context of compressive sensing is that signals exhibit a degree of structure. Here, it is important to note that there is a difference between signal sparisty and signal compressibility. The signal is considered sparse if it has only a few non-zero values in comparison with its overall length. However, it is considered compressible if it’s sorted coefficient magnitudes decays rapidly. To consider this mathematically, let x be a signal which is compressible in the basis![]() ,
,![]() , where
, where ![]() are the coefficients of x in the basis Ψ. If x is compressible, then the magnitudes of the sorted coefficients observe power law decay;
are the coefficients of x in the basis Ψ. If x is compressible, then the magnitudes of the sorted coefficients observe power law decay;![]() ,
, ![]() signal is defined as being compressible if it obeys this power law decay. The larger q is, the faster the magnitudes decay, and the more compressible a signal is.
signal is defined as being compressible if it obeys this power law decay. The larger q is, the faster the magnitudes decay, and the more compressible a signal is.
5.1. The Time-Domain Representation
Generally, the time-domain representation of most signals has low signal sparisty. Thus, these signals are not the true signals but their representations under a certain basis are sparse or compressible. ECG signal is an example of such signals. Various researchers have reported ECG signals to be sparse in other bases [7] [8] . A variety of compression algorithms represent ECG signals in suitable or thogonal basis and exploit signal redundancy in the transformed domain. Indeed, success of a compression algorithm depends on how compactly the signal is re- presented upon transformation. In this context, many transforming methods for representing signals in sparsity bases are proposed recently, for instance, FFT, DWT and DCT, etc. Generally, the biophysical signals are con-
tinuous and regular in nature. Hence, it can be represented by aforementioned transforms. Every transformation basis is able to provide a way of recovering the signal and should provide a way for retrieving diagnostic information from the signal to form patient’s report of the medical case study. This section introduces the three transformation techniques used for controlling signals’ sparsity.
5.2. Discrete Fourier Transform
Discrete Fourier Transform (DFT) is a fundamental transform in digital signal processing with applications in frequency analysis, signal processing etc. DFT is the transformation of the discrete signal taking in time domain into its discrete frequency domain representation. The periodicity and symmetry properties of DFT are useful for compression. The nth DFT coefficient of length N sequence ![]() is defined as follows:
is defined as follows:
![]() (12)
(12)
And its inverse transform (IDFT) as
![]() (13)
(13)
The number of complex multiplications and additions to compute DFT is![]() . Moreover fast algorithms exist that makes it possible to compute DFT efficiently [1] . This algorithm is popularly known as Fast Fourier Transform (FFT) which reduces the computational burden to
. Moreover fast algorithms exist that makes it possible to compute DFT efficiently [1] . This algorithm is popularly known as Fast Fourier Transform (FFT) which reduces the computational burden to![]() . FFT is computational efficient algorithms to compute the DFT and its inverse. FFT requires the number of data points to be a power of 2 (usually padding is used to make this true). The functions
. FFT is computational efficient algorithms to compute the DFT and its inverse. FFT requires the number of data points to be a power of 2 (usually padding is used to make this true). The functions ![]() and
and ![]() implement the transform and inverse trans- form pair given for vectors of length N by:
implement the transform and inverse trans- form pair given for vectors of length N by:
![]() (14)
(14)
![]() (15)
(15)
5.3. Discrete Cosine Transformation
DCT is a technique for converting a signal into elementary frequency components. It expresses a sequence of finitely numerous data points in terms of a sum of cosine functions oscillating at different frequencies which is widely used in image compression. DCT has the following properties:
It is closely related to the DFT with some dissimilarity.
It is more efficient in concentrating energy into lower order coefficients than the DFT.
It is purely real whereas the DFT is complex (magnitude and phase).
In case of image processing, coefficients produced by a DCT operation on a block of pixels are similar to the frequency domain coefficients produced by a DFT operation. As an N point DCT is closely related to a 2N-point DFT, it has the same frequency resolution. The N frequencies of a 2N point DFT correspond to N points on the upper half of the unit circle in the complex frequency plane. Unlike DCT, the magnitude of the DFT coefficients is spatially invariant (phase of the input does not matter) assuming a periodic input. For processing one-dimen- sional signals such as ECG waveforms one-dimensional DCT is used. For analysis of two dimensional (2D) signals such as images, a 2D version of the DCT is required. As the 2-Dimensional DCT can be computed by applying 1D transforms separately to the rows and columns, it can be said that the 2D DCT is separable in the two dimensions.
The DCT is currently widely used for compressing data such as images (JPEG), video (MPEG) and audio (MP3). It is a basis for many signal and image compression algorithms due to its high decorrelation and energy compaction property. In this paper, DCT is adopted for compressing ECG signals based on CS approach. A DCT of N samples signal is defined as
![]() (16)
(16)
where ![]() for
for ![]() and
and ![]() otherwise. The function
otherwise. The function ![]() represents the value of nth samples of input signals and
represents the value of nth samples of input signals and ![]() represents DCT coefficients. The inverse DCT is defined in similar fashion as
represents DCT coefficients. The inverse DCT is defined in similar fashion as
![]() (17)
(17)
Since DCT belongs to family of DFT there are Fast DCT algorithms of computational complexity N log2 N similar to FFT. Using this equation, it is possible to transform the original signal into a spatial domain to be adopted in the proposed CS compression technique [11] .
5.4. Discrete Wavelet Transformation
By using mathematical transforms such as the FFT or DCT, it is possible to compress data to a very high degree. But, however, these processes usually require large computing efforts. Moreover, the two transforms deals with stationary signals. The wavelet transform describes a multi-resolution decomposition process in terms of expansion of a signal onto a set of wavelet basis functions. Wavelet transforms have become an attractive and efficient tool in many applications especially in coding and compression of signals because of multi-resolution and high-energy compaction properties. Wavelets allow both time and frequency analysis of signals simultaneously because of the fact that energy of wavelet is concentrated in time and still possesses the wave like characteristics.
DWT has its own excellent space frequency localization property. The key issues in DWT and inverse DWT are signal decomposition and reconstruction, respectively. The basic idea behind decomposition and reconstruction is low-pass and high-pass filtering with the use of down sampling and up sampling respectively. The result of wavelet decomposition is hierarchically organized decompositions. One can choose the level of decomposition ![]() based on a desired cutoff frequency. Figure 6(a) shows an implementation of a three-level forward DWT based on a two-channel recursive filter bank, where
based on a desired cutoff frequency. Figure 6(a) shows an implementation of a three-level forward DWT based on a two-channel recursive filter bank, where ![]() and
and ![]() are low-pass and high-pass ana- lysis filters, respectively, and the block $2 represents the down sampling operator by a factor of 2. The input signal
are low-pass and high-pass ana- lysis filters, respectively, and the block $2 represents the down sampling operator by a factor of 2. The input signal ![]() is recursively decomposed into a total of four subband signals: a coarse signal
is recursively decomposed into a total of four subband signals: a coarse signal![]() , and three detail signals,
, and three detail signals, ![]() ,
, ![]() , and
, and![]() , of three resolutions. Figure 6(b) shows an implementation of a three-level inverse DWT based on a two-channel recursive filter bank, where
, of three resolutions. Figure 6(b) shows an implementation of a three-level inverse DWT based on a two-channel recursive filter bank, where ![]() and
and ![]() are low-pass and high-pass synthesis filters, respectively, and the block #2 represents the up sampling operator by a factor of 2. The four subband signals
are low-pass and high-pass synthesis filters, respectively, and the block #2 represents the up sampling operator by a factor of 2. The four subband signals![]() ,
, ![]()
![]() and
and![]() , are recursively combined to reconstruct the output signal
, are recursively combined to reconstruct the output signal![]() . The four finite impulse response filters satisfy the following relationships:
. The four finite impulse response filters satisfy the following relationships:
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
so that the output of the inverse DWT is identical to the input of the forward DWT.
6. Signal Reconstruction Algorithms
Compressive sensing is a sampling method which provides a new approach to efficient signal compression and recovery by exploiting the fact that a sparse signal can be suitably reconstructed from very few measurements. One of the most concerns in compressive sensing is the construction of the sensing matrices. While random sensing matrices have been widely studied, only a few deterministic sensing matrices have been considered. These matrices are highly desirable on structure which allows fast implementation with reduced storage requirements. In this section, a survey of deterministic sensing matrices for compressive sensing is presented. We introduce a basic problem in compressive sensing and some disadvantage of the random sensing matrices. Some recent results on construction of the deterministic sensing matrices are discussed.
The solution of the CS problem consists of two steps. In the first step, we design a stable measurement matrix that ensures that the main information in any K-sparse or compressible signal is not damaged by the dimensiona-
![]() (a)
(a)![]() (b)
(b)
Figure 6. A three-level two-channel iterative filter bank (a) forward DWT; (b) inverse DWT.
lity reduction from ![]() down to
down to![]() . In the second step, a reconstruction algorithm should be developed to recover x from the measurements y. In [3] [4] , it has been shown that a sparse signal can be reconstructed from very few measurements by solving the CS problem via one of the following minimization strategies:
. In the second step, a reconstruction algorithm should be developed to recover x from the measurements y. In [3] [4] , it has been shown that a sparse signal can be reconstructed from very few measurements by solving the CS problem via one of the following minimization strategies:
![]() minimization strategy
minimization strategy
![]() (21)
(21)
![]() minimization strategy
minimization strategy
![]() (22)
(22)
![]() minimization strategy: adopting a strategy between
minimization strategy: adopting a strategy between ![]() minimization and
minimization and ![]() minimization
minimization
![]() (23)
(23)
The sufficient conditions for having the solution of ![]() minimization to coincide with that of
minimization to coincide with that of ![]() minimization are dependent on either mutual coherence or RIP. These conditions are closely related to each other and play an important role in the construction of sensing matrices. To investigate this relation, consider
minimization are dependent on either mutual coherence or RIP. These conditions are closely related to each other and play an important role in the construction of sensing matrices. To investigate this relation, consider ![]() as an
as an ![]() sensing matrix.
sensing matrix. ![]() it has been mentioned by Candes and Donoho, the existence and uniqueness of the solution of any of the above mentioned minimization problems can be guaranteed as soon as the measurement matrix A satisfies the RIP of order s. Suppose that there exists a constant
it has been mentioned by Candes and Donoho, the existence and uniqueness of the solution of any of the above mentioned minimization problems can be guaranteed as soon as the measurement matrix A satisfies the RIP of order s. Suppose that there exists a constant ![]() such that, for every
such that, for every ![]() sub- matrix
sub- matrix ![]() of A and for every vector y,
of A and for every vector y,
![]() (24)
(24)
Then, the matrix A is said to satisfy the s-restricted isometry property with Restricted Isometry Constant (RIC)![]() . A strict condition
. A strict condition ![]() also guarantees exact solution via
also guarantees exact solution via ![]() -minimization. However, the
-minimization. However, the ![]() -minimi- zation problem remains NP-hard; that is, it cannot be solved in practice. For
-minimi- zation problem remains NP-hard; that is, it cannot be solved in practice. For![]() , there is no numerical scheme to compute solutions with minimal
, there is no numerical scheme to compute solutions with minimal ![]() -norm as well. Furthermore, the
-norm as well. Furthermore, the ![]() -minimization problem is a convex optimization problem, and in fact, it can be formulated as a linear optimization problem. Then solving via
-minimization problem is a convex optimization problem, and in fact, it can be formulated as a linear optimization problem. Then solving via ![]() -minimization is efficient with high probability. Hence, most researchers are interested in the recovery via
-minimization is efficient with high probability. Hence, most researchers are interested in the recovery via ![]() - minimization. There are two common ways to solve these problems. First, we can exactly recover
- minimization. There are two common ways to solve these problems. First, we can exactly recover ![]() via
via ![]() - minimization by solving this problem with allowable error
- minimization by solving this problem with allowable error![]() , which is given as
, which is given as
![]() (25)
(25)
The second method is using greedy algorithms for ![]() -minimization, such as Matching Pursuit (MP), Orthogonal Matching Pursuit (OMP), or their modifications [12] . However, in order to ensure unique and stable reconstruction, the sensing matrix
-minimization, such as Matching Pursuit (MP), Orthogonal Matching Pursuit (OMP), or their modifications [12] . However, in order to ensure unique and stable reconstruction, the sensing matrix ![]() must satisfy some criteria. One of the well-known criteria is 2𝑘-RIP.
must satisfy some criteria. One of the well-known criteria is 2𝑘-RIP.
7. Sensing Matrices in Compressive Sensing
In technical literature, more attention has been paid to random sensing matrices generated by identical and independent distributions (i.i.d.) such as Gaussian, Bernoulli, and random Fourier ensembles, to name a few [11] [13] . Their applications have been shown in medical images processing and other various signal processing problems [10] . Even though random sensing matrices ensure high probability in reconstruction, they also have many drawbacks such as excessive complexity in reconstruction, significant space requirement for storage, and no efficient algorithm to verify whether a sensing matrix satisfies RIP property with small RIC value. Hence, exploiting specific structures of deterministic sensing matrices is required to solve these problems of the random sensing matrices. Recently, several deterministic sensing matrices have been proposed [14] - [16] . We can classify them into two categories. First are those matrices which are based on coherence [14] . Second are those matrices which are based on RIP or some weaker RIPs [15] . More recently in [16] some highlighted results such as deterministic construction of sensing matrices via algebraic curves over finite fields in term of coherence and chirp sensing matrices have been introduced. Table 1 illustrates the comparison between random sensing and deterministic sensing.
![]()
Table 1. Comparison between random sensing and deterministic sensing.
7.1. Random Sensing Matrices and Their Drawbacks
Recall that ![]() is the vector we want to recover. Because the number of measurements is much smaller than its dimension
is the vector we want to recover. Because the number of measurements is much smaller than its dimension![]() , we cannot find a linear identity reconstruction map; that is, unique solution does not exist for all
, we cannot find a linear identity reconstruction map; that is, unique solution does not exist for all ![]() in
in![]() . In general, random matrices are easy to construct and ensure high probability reconstruction. However, they also have many drawbacks. First, storing random matrices requires a lot of storage. Second, there is no efficient algorithm verifying RIP condition for such matrices. So far, it is not a good approach because of its lack of efficiency. The recovery problems may be difficult when the dimension of the signal becomes large, and we have to construct a measurement matrix that satisfies RIP with a small δ(s).
. In general, random matrices are easy to construct and ensure high probability reconstruction. However, they also have many drawbacks. First, storing random matrices requires a lot of storage. Second, there is no efficient algorithm verifying RIP condition for such matrices. So far, it is not a good approach because of its lack of efficiency. The recovery problems may be difficult when the dimension of the signal becomes large, and we have to construct a measurement matrix that satisfies RIP with a small δ(s).
By now, many papers deal with Gaussian or Bernoulli random matrices in connection with sparse recovery [13] . The entries of a random Bernoulli matrix take the values ![]() or
or ![]() with equal probability. However, the entries of a Gaussian matrix are independent and follow a normal distribution with expectation 0 and variance
with equal probability. However, the entries of a Gaussian matrix are independent and follow a normal distribution with expectation 0 and variance![]() . With high probability such random matrices satisfy the RIP with a (near) optimal order, and therefore allow sparse recovery using
. With high probability such random matrices satisfy the RIP with a (near) optimal order, and therefore allow sparse recovery using ![]() minimization. Moreover, these matrices have the disadvantage that no fast matrix multiplication, that may speed up recovery algorithms significantly, is available. Thus, large scale problems are not practicable with Gaussian or Bernoulli matrices and storing an unstructured matrix may be difficult.
minimization. Moreover, these matrices have the disadvantage that no fast matrix multiplication, that may speed up recovery algorithms significantly, is available. Thus, large scale problems are not practicable with Gaussian or Bernoulli matrices and storing an unstructured matrix may be difficult.
7.2. Deterministic Sensing Matrices
In [11] , various deterministic sensing matrices have been investigated and presented in terms of coherence and RIP. The advantages of these matrices, in addition to their deterministic constructions, are the simplicity in sampling and recovery process as well as small storage requirement. These methods include:
Chirp sensing matrices.
Second-order Reed-Muller sensing matrices.
Binary bch matrices.
Sensing matrices with statistical restricted isometry property.
Deterministic construction of sensing matrices via algebraic curves over finite fields.
Binary sensing matrices generated by unbalanced expander graphs.
It can be possible to make further improvement in both reconstruction efficiency and accuracy using these deter- ministic matrices in compressive sensing, particularly when some a priori information on location of non-zero components is available.
8. Applications of Compressive Sensing
When a signal is sparse, most of its coefficients is zero, or they are small enough to be ignored without much perceptual loss. Fortunately, in many applications such as wireless sensors, cognitive radios or medical imagers, the signals of interests have sparse representations in some signal domain [17] . For example, in a cognitive radio application, the signal of interest is sparse in the frequency domain since at any one time only a few percentages of total available channels are occupied by users. Also radar imaging seems to be a very promising application of compressive sensing techniques [18] . One is usually monitoring only a small number of targets, so that sparsity is a very realistic assumption. Standard methods for radar imaging actually also use the sparsity assumption, but only at the very end of the signal processing procedure in order to clean up the noise in the resulting image. Us- ing sparsity systematically from the very beginning by exploiting compressive sensing methods is therefore a natural approach. Further potential applications include image processing [19] , and analog to digital conversion [20] .
8.1. Medical Applications of CS
In medical field, bio-signals such as ECG signals are sparse in either Fourier or wavelet domain which makes them good candidate for CS. In computerized tomography, for instance, one would like to obtain an image of the inside of a human body by taking X-ray images from different angles. Taking an almost complete set of images would expose the patient to a large and dangerous dose of radiation, so the amount of measurements should be as small as possible, and nevertheless guarantee a good enough image quality. Such images are usually nearly piecewise constant and therefore nearly sparse in the gradient, so there is a good reason to believe that compres- sive sensing is well applicable [17] .
The traditional process of medical imaging and compression is quite costly. It acquires the entire signal at beginning, then does the compression and throws most of the information away at the end. The new idea of the signal compression combines signal acquisition and compression as one step which improves the overall cost significantly. Compressed sensing captures and represents signals and images at a rate significantly below Nyquist rate. Compressed sensing breaks the canonical rules and effectively reduces the sampling rate without losing the essential information, so it has a wide application in medical applications. By testing the MRI images, both algorithms can provide satisfactory results when the images are smooth. But when the images are rough or have a lot of details, the recovery results are not good. This kind of images needs more measurements to recon- struct the images [21] [22] .
8.2. Wireless Sensor Networks Applications of CS
Wireless sensor networks (WSNs) are critically resource constrained by limited power supply, memory, pro- cessing performance and communication bandwidth [23] . Due to their limited power supply, energy consump- tion is a key issue in the design of protocols and algorithms for WSNs. Energy efficiency are necessary in every level of WSN operations (e.g., sensing, computing, and transmission). In the conventional view, energy consumption in WSNs is dominated by radio communications [24] . The energy consumption of radio communication mainly depends on the number of bits of data to be transmitted within the network. In most cases, computational energy cost is insignificant compared to communication cost. For instance, the energy cost of transmitting one bit is typically around 500 - 1000 times greater than that of a single 32-bit computation [25] . Therefore, using compression to reduce the number of bits to be transmitted has the potential to drastically reduce communication energy costs and increase network lifetime. Thus, researchers have investigated optimal algorithms for the compression of sensed data, communication and sensing in WSNs [26] . Most existing data-driven energy management and conservation approaches for WSNs target reduction in communications energy at the cost of increased computational energy [26] . In principle, compression techniques work on reducing the number of bits needed to represent the sensed data, not on the reducing the amount of sensed data; hence, they are unable to utilize sensing energy costs efficiently in WSNs. Importantly, in most cases, these approaches assume that sensing operations consume less energy than radio transmission and reception [27] .
Sensing of the application environment is the main purpose of a wireless sensor network. Most existing energy management strategies and compression techniques assume that the sensing operation consumes significantly less energy than radio transmission and reception. This assumption does not hold in a number of practical applications. Sensing energy consumption in these applications may be comparable to, or even greater than, that of the radio. In [28] , a quantitative analysis of the main operational energy costs of popular sensors, radios and sensor motes supports this claim. Compressed sensing and distributed compressed sensing have been adopted as potential approaches to provide energy efficient sensing in wireless sensor networks.
8.3. Single-Pixel Compressive Digital Camera
Single-pixel compressive digital camera directly acquires M random linear measurements without first collecting the N pixel values [29] as shown in Figure 7. The incident light field corresponding to the desired image x is not focused onto a CMOS sampling array but rather reflected off a Digital Micro-mirror Device (DMD) consisting of an array of N tiny mirrors. DMDs are found inside many computer projectors and projection televisions. The reflected light is then collected by a second lens and focused onto a single photodiode (the single pixel). Each mirror can be independently oriented either towards the photodiode (corresponding to a 1) or away from the photodiode (corresponding to a 0). Each measurement ![]() is obtained as follows: The random number
is obtained as follows: The random number
![]()
Figure 7. Single-pixel, compressive sensing camera.
generator (RNG) sets the mirror orientations in a pseudorandom 0/1 pattern to create the measurement vector![]() . The voltage at the photodiode then equals
. The voltage at the photodiode then equals![]() , the inner product between
, the inner product between ![]() and the desired image x. The process is repeated M times to obtain all of the entries in y. A major advantage of the single-pixel, compressive sensing approach is that this camera can be adapted to image at wavelengths where it is difficult or expensive to create a large array of sensors. It can also acquire data over time to enable video reconstruction [29] .
and the desired image x. The process is repeated M times to obtain all of the entries in y. A major advantage of the single-pixel, compressive sensing approach is that this camera can be adapted to image at wavelengths where it is difficult or expensive to create a large array of sensors. It can also acquire data over time to enable video reconstruction [29] .
9. Illustrative Numerical Examples
In this section three illustrative examples are given to demonstrate the compressive sensing process. Matlab version 8.1 has been adopted for developing the codes used in getting the results. In the three examples L1-magic software code is used to recover the signal. This software is freely available from the website http://www.acm.caltech.edu/l1magic/. The Matlab codes of the first two examples can be downloaded freely from http://compsens.eecs.umich.edu/sensing_tutorial.php. The first example deals with the signal sparse in frequency- domain and hence random measurements are taken in time-domain. The second example deals with the signal sparse in time domain and the random measurements are taken in the frequency domain. The third example demonstrates the spikes signal case.
Example 1: Signal Sparse in Frequency
This code demonstrates the compressive sensing using a sparse signal in frequency domain. The signal consists of the summation of two sinusoids of different frequencies in time domain; ![]() with
with ![]() samples and
samples and![]() . Figure 8(a) illustrates the time-domain signal, and its DFT spectrum. The signal is sparse in frequency domain and therefore 400 random measurements are taken in time domain adopting random measurements DFT matrix. Using the L1-magic software, the 1024 samples signal is recovered from the 400 measurements. Figure 8(b) shows the recovered signal spectrum along with the recovered time- domain signal. Figure 9 illustrates the difference between the recovered and the original time-domain signals.
. Figure 8(a) illustrates the time-domain signal, and its DFT spectrum. The signal is sparse in frequency domain and therefore 400 random measurements are taken in time domain adopting random measurements DFT matrix. Using the L1-magic software, the 1024 samples signal is recovered from the 400 measurements. Figure 8(b) shows the recovered signal spectrum along with the recovered time- domain signal. Figure 9 illustrates the difference between the recovered and the original time-domain signals.
Example 2: Signal Sparse in Time
This example demonstrates the compressive sensing of a signal sparse in the time domain. The signal consists of a UWB (Ultra Wide Band) pulse in time domain with 4 GHz RF frequency, 16 GHz pulse repetition frequency and 16 GHz sampling frequency. In this case, 90 random measurements are taken in frequency domain from 500 possible coefficients. Figure 10(a) and Figure 10(b) show the time domain signal and its DFT. Using the L1- magic software, the 500 samples signal is recovered from the 90 measurements. Figure 10(c) and Figure 10(d) show the recovered time-domain signal and the difference between the original and recovered signals.
Example 3: Sparse in spikes signal
This example demonstrates the compressive sensing of a spikes sparse signal. The signal length ![]() and the number of spikes in the signal
and the number of spikes in the signal ![]() samples distributed randomly along the signal. For CS test, only
samples distributed randomly along the signal. For CS test, only ![]() observations are used. Figure 11(a) and Figure 11(b) illustrate the original time-domain signal and the recovered signal (after CS) respectively. Figure 12 shows the difference between the spikes signal before and after CS.
observations are used. Figure 11(a) and Figure 11(b) illustrate the original time-domain signal and the recovered signal (after CS) respectively. Figure 12 shows the difference between the spikes signal before and after CS.
10. Information Sources
The initial papers on CS subject are [3] [4] . An introduction to compressive sensing is contained in the monograph [30] by Rauhut and Foucart. Another introductory source is the lecture notes of the summer school
![]()
Figure 9. Difference between the recovered and the original time- domain signals.
![]()
![]() (a) (b)
(a) (b)
Figure 11. CS of spikes sparse signal. (a) Original time-domain signal; (b) Recovered signal after CS.
![]()
Figure 12. Difference between the spikes signal before and after CS.
“Theoretical Foundations and Numerical Methods for Sparse Recovery”, held at RICAM in 2009 [31] [32] . The overview papers [33] - [36] introduce various theoretical and applied aspects of compressive sensing. A large collection of the vastly growing research on CS is available on the webpage http://www.compressedsensing.com.
The other two most visited sources of information are the compressed sensing resource webpage maintained by Richard Baraniuk and his team at the Rice University [37] and Nuit Blancheblog of Igor Carron [11] . The first link lists and classifies new preprints, papers, tutorial and software in the field, often from the personal announcements of the authors. Blanche is realizing the same task than the first link but in addition his author comments the content of added research topics, trying to link certain of these to others, observing some new trends in the theory, disseminating the different software and tool boxes guaranteeing the reproducibility of the experiments. Many other blogs exist in related topics to CS and it could be difficult to list the mall here. We can mention for instance the applied mathematics blog “What’s new” by Terence Tao [38] . The advent of compressed sensing theory is also related to a free dissemination of the numerical codes helping the community to reproduce experiments. A lot of tool boxes have therefore been produced in different languages: C, C++, Matlab and Python [37] -[39] .