On Exact Solutions of Second Order Nonlinear Ordinary Differential Equations ()
1. Introduction
Exact solutions have always played and still play an important role in properly understanding the qualitative features of many phenomena and processes in various fields of natural science. Exact solutions of nonlinear equations, including those without a clear physical sense which do not correspond to real phenomena and pro- cesses, play an important role of test problems for verifying the correctness and assessment of accuracy of various numerical, asymptotic, and approximate methods. Moreover, the model equations admitting exact solutions serve as the basis for the development of new numerical, asymptotic, and approximate methods, which, in turn, enable us to study more complicated problems having no analytical solutions [1] . In the paper [2] , Laith and Nama introduced a new approach for solving second order linear differential equation with variable coefficients
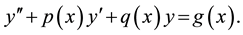 (1)
(1)
To look for exact solution of (1) the authors introduced the substitution
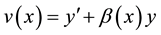 (2)
(2)
and have looked for a solution of the Riccati equation
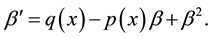 (3)
(3)
In this paper, we generalize the idea of [2] and propose a general approach for solving the nonlinear second order equation
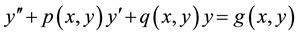 (4)
(4)
which can be written as
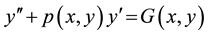 (5)
(5)
where 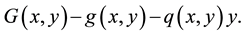
2. The Main Results
In this section, we propose an algorithm that enables us to reduce the Equations (4) and (5) by looking for solutions of the partial differential equations
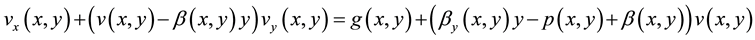 (6)
(6)
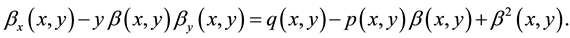 (7)
(7)
Theorem 1. If v(x; y) is any solution of (6) where (x; y) is a solution of (7), then Equation (4) can be reduced to a first order equation.
Proof. In order to prove this theorem, consider the transformation
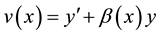 (8)
(8)
if we differentiate both sides of (8) with respect to x we obtain
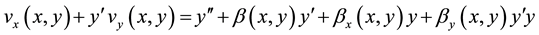 (9)
(9)
substituting (4) and (8) in (9), we have
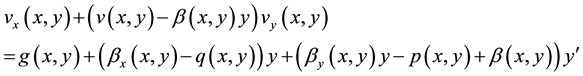 (10)
(10)
assuming that 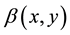 is a solution of (7), Equation (10) can be reduced to (6), solving (6) for
is a solution of (7), Equation (10) can be reduced to (6), solving (6) for 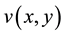 we have the result. ■
we have the result. ■
Theorem 2. If 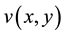 is any solution of the equation
is any solution of the equation
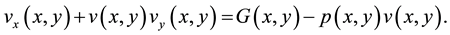 (11)
(11)
Then (5) can be reduced to a first equation.
Proof. From theorem (1) the associated equation with 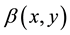 is
is
![]() (12)
(12)
which has a solution![]() , thus the equation associated with
, thus the equation associated with ![]() is (11), solving for
is (11), solving for ![]() Equation (5) reduced to a first order equation. ■
Equation (5) reduced to a first order equation. ■
Theorem 3. If ![]() is any solution of the equation
is any solution of the equation
![]() (13)
(13)
Then Equation (5) can be reduced to first order equation.
Proof. Equation (5) can be written as
![]() (14)
(14)
applying theorem (1), we have that ![]() is a solution of
is a solution of
![]() (15)
(15)
solving (13) for![]() , the result follows. ■
, the result follows. ■
Theorem 4. If![]() , then Equation (5) can be reduced to a first order equation.
, then Equation (5) can be reduced to a first order equation.
Proof. Applying theorem (2) the result follows. ■
3. Examples
In this section, we give some examples on our approach for reduction and finding solutions of nonlinear second order ordinary differential equations, these equations and more equations that can be easily solved by this method can be found in [1] [3] - [7] .
Example 1. Consider the equation
![]() (16)
(16)
comparing with Equation (4) we note that![]() ,
, ![]() ,
,![]() .
.
First, we solve
![]() (17)
(17)
the associated ratios with Equation (17) are
![]()
from which, we find that ![]()
Second, we solve
![]() (19)
(19)
the associated ratios with Equation (19) are
![]() (20)
(20)
from which, we find that ![]()
Finally, we substitute![]() ,
, ![]() in Equation (8) to get
in Equation (8) to get
![]() (21)
(21)
Example 2. Consider the equation
![]() (22)
(22)
this equation can be written as
![]() (23)
(23)
comparing with Equation (5) we have that![]() ,
, ![]() ,
,![]() .
.
The equation associated with ![]() is
is
![]() (24)
(24)
from which we find that![]() . The equation associated with
. The equation associated with ![]() is
is
![]() (25)
(25)
we look for a solution of the form
![]() (26)
(26)
substituting ![]() in Equation (25), we have
in Equation (25), we have
![]() (27)
(27)
Thus, ![]() and
and ![]() must satisfy the following equations
must satisfy the following equations
![]() (28)
(28)
![]() (29)
(29)
![]() (30)
(30)
from which we find that
![]() (31)
(31)
![]() (32)
(32)
so,![]() . Finally we solve
. Finally we solve
![]() (33)
(33)
and two cases are considered,
![]() , the solution is
, the solution is ![]() (34)
(34)
![]() , the solution is
, the solution is ![]() (35)
(35)
Example 3. Consider the equation
![]() (36)
(36)
Equation (36) can be written as
![]() (37)
(37)
Comparing with Equation (5) we have![]() ,
, ![]() , furthermore
, furthermore
![]() . So, theorem (4) can be applied as follows:
. So, theorem (4) can be applied as follows:
![]() (38)
(38)
which implies that
![]() (39)
(39)
Differentiating both sides of (39), we have
![]() (40)
(40)
Assuming that![]() , yields
, yields
![]() (41)
(41)
thus, Equation (36) reduced to the first order exact ordinary differential equation
![]() (42)
(42)
which has the solution
![]() (43)
(43)
4. Conclusion
In this article, a new method is considered for solving second order nonlinear ordinary differential equations. The small size of computation in comparison with the computational size required by other analytical methods [1] , and the dependence on first order partial differential equations show that this method can be improved and introduces a significant improvement in solving this type of differential equations over existing methods. This method is proposed to be considered as an alternative approach being employed to a wide variety of equations.