1. Introduction
The Kuhn-Tucker conditions have been used to derive many significant results in economics, particularly in decision problems that occur in static situations, for instance, to show the existence of an equilibrium for a competitive economy (Negishi [1] ), to carry out the first-order approach to principal-agent problems (Rogerson [2] ), and to examine the need for land reform (Grossman [3] ). Also, the Kuhn-Tucker conditions and/or the method of Lagrange multipliers are usually contained in standard microeconomics textbooks, for instance, Mas-Colell, Whinston and Green [4] , where the Kuhn-Tucker conditions for the problem with both inequality and equality constraints are discussed.
The Kuhn-Tucker conditions for the optimization problem with inequality and equality constraints have a comprehensive form that incorporates the method of Lagrange multipliers (introduced by Lagrange in 1788) in a natural way; therefore, the simple derivation of the Kuhn-Tucker conditions would shed light on the problem’s true nature.
In this paper, the Kuhn-Tucker conditions under the Mangasarian-Fromovitz constraint qualification are derived directly by applying a corollary of Farkas’s lemma without resorting to the Fritz John conditions and the boundedness of Lagrange multipliers is also shown.
2. Preliminaries
The problem to be addressed is as follows:
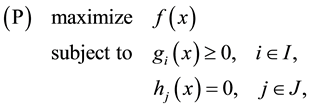
where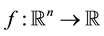 ,
,  , and
, and 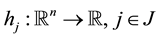 are continuously Fréchet differentiable functions, and
are continuously Fréchet differentiable functions, and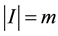 ,
, 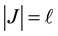 (
( ). If there are no inequality (equality) constraints, we think that
). If there are no inequality (equality) constraints, we think that 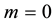 (
(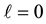 ).
).
Here, we should pay attention to the fact that the problem (P) naturally includes the optimization problem with equality constraints considered by Lagrange in the 18th century.
We postulate the following Mangasarian-Fromovitz constraint qualification (MF) (Mangasarian and Fromovitz [5] ) in association with (P). We define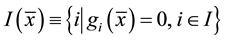 .
.
(MF) For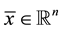 ,
, 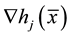 ,
,  are linearly independent, and there exists an
are linearly independent, and there exists an 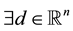 s.t.
s.t.  and
and .
.
Remarks
The linearly independent constraint qualification, which is usually assumed in practice, implies (MF) (see Nocedal and Wright [6] ).
(MF) is equal to the Cottle constraint qualification without the presence of equality constraints, and if the problem (P) is a concave program without equality constraints, the Slater constraint qualification implies the Cottle constraint qualification (Bazaraa and Shetty [7] ).
Finally, we recall the following result to the linear system including equalities for the sake of convenience.
Lemma 1. ([7] , Corollary 2 to Theorem 2.3.5) For![]() ,
, ![]() , and
, and![]() , either
, either
(a)![]() ,
, ![]() ,
, ![]() ,
,
or
(b)![]() ,
, ![]() and
and![]() ,
, ![]()
but never both. ![]()
3. Result
We now establish the main result, which differs from [7] Theorem 5.3.1 in that our result includes complementarity conditions and the boundedness of Lagrange multipliers under (MF).
Theorem 1. Suppose that ![]() is a local solution for (P), and that the constraint qualification (MF) holds at
is a local solution for (P), and that the constraint qualification (MF) holds at![]() . Then, it holds that for
. Then, it holds that for ![]() and
and![]() ,
,
![]() (1)
(1)
![]()
and![]() ,
, ![]() are bounded.
are bounded.
Proof. At a local solution![]() , if we choose
, if we choose ![]() in the feasible region such that
in the feasible region such that![]() ,
,
![]()
![]()
which shows that ![]() satisfies
satisfies![]() ,
, ![]() and
and![]() ,
,![]() .
.
Then, for a local solution![]() , it follows that
, it follows that
![]() (2)
(2)
does not hold, since, if so, ![]() as
as ![]() for
for![]() , which con-
, which con-
tradicts the local optimality of ![]() at
at![]() .
.
Note that (MF) guarantees the existence of such ![]() from the implicit function theorem ([8] , Appendix D-3 with
from the implicit function theorem ([8] , Appendix D-3 with ![]() and
and![]() ) if
) if![]() ; otherwise (2) does not hold for
; otherwise (2) does not hold for![]() . By applying Lemma 1 to (2) and (MF), even if the active constraints are empty, we obtain
. By applying Lemma 1 to (2) and (MF), even if the active constraints are empty, we obtain
![]() (3)
(3)
or, equivalently,
![]()
for![]() ,
,![]() .
.
The rest part of the proof is as follows. From (3) we obtain
![]()
So, if![]() ,
,
![]()
and if![]() ,
, ![]() vanishes. In any case, (3) reduced to
vanishes. In any case, (3) reduced to
![]()
Since![]() ,
, ![]() are linearly independent by (MF),
are linearly independent by (MF), ![]() is determined to a single bounded vector.
is determined to a single bounded vector. ![]()
Example 1.
Consider the problem
![]()
with an optimal solution![]() . At
. At![]() , the linearly independent constraint qualification does not hold, whereas (MF) holds for
, the linearly independent constraint qualification does not hold, whereas (MF) holds for![]() .
.
Indeed, (MF) is valid for problems with a number of inequality constraints and admits feasible directions around ![]() in the orthogonal complementary space of
in the orthogonal complementary space of![]() ,
,![]() .
.
4. Concluding Remarks
In this paper, the Kuhn-Tucker conditions under the Mangasarian-Fromovitz constraint qualification were derived directly by applying a corollary of Farkas’s lemma without resorting to the Fritz John conditions, or without introducing the Bouligand tangent cone, and the boundedness of Lagrange multipliers was also shown.
Considerable effort has been devoted to the generalization of Farkas’s lemma. However, what seems to be lacking is a discrete version of Farkas’s lemma under a mild condition; such a version would be theoretically meaningful and would be help solve the discrete optimization problems that emerge in the economics studying indivisible goods.