1. Introduction
In physics, the uncertainty principle plays an important role in elementary fields, and data concentration is often considered carefully via the uncertainty principle [1] - [8] . In continuous signals, the supports are assumed to be
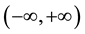 , based on which various uncertainty relations [1] [2] [9] - [21] have been presented. However, in practice, both the supports of time and frequency are often limited. In such case, the support
, based on which various uncertainty relations [1] [2] [9] - [21] have been presented. However, in practice, both the supports of time and frequency are often limited. In such case, the support 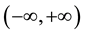 fails to hold
fails to hold
true. In limited supports, some papers such as [22] - [25] have discussed the uncertainty principle in conventional time-frequency domains for continuous and discrete cases and some conclusions are achieved. However, none of them has covered the linear canonical transform (LCT) in terms of Heisenberg uncertainty principles that have been widely used in various fields [4] - [6] . Therefore, there has a great need to discuss the uncertainty relations in LCT domains. As the generalization of the traditional FT, FRFT [5] [6] [26] - [28] and so on, LCT has some special properties with more transform parameters (or freedoms) and sometimes yields the better result [29] . Readers can see more details on LCT in [6] and so on.
2. Preliminaries
2.1. Definition of LCT
Before discussing the uncertainty principle, we will introduce some relevant preliminaries. Here, we first briefly
review the definition of LCT. For given continuous signal 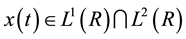 and
and , its LCT [6] is defined as
, its LCT [6] is defined as
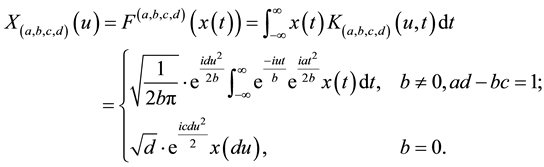 (1)
(1)
where 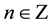 and
and  is the complex unit,
is the complex unit, 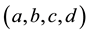 are the transform parameters defined as that in [6] . In addition,
are the transform parameters defined as that in [6] . In addition,  and
and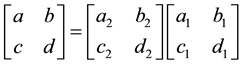 . If
. If 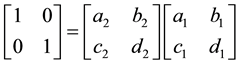 , then
, then 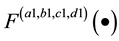 and
and 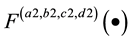 are the LCT transform pairs, i.e.,
are the LCT transform pairs, i.e.,  . Also, if
. Also, if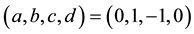 , we have the following equations:
, we have the following equations:
 and.
and.
However, unlike the discrete FT, there are a few definitions for the DLCT (discrete LCT), but not only one. In this paper, we will employ the definition defined as follows [6] :
![]() (2)
(2)
Clearly, if![]() , (2) reduces to the traditional discrete FT [6] . Also, we can rewrite definition (2) as
, (2) reduces to the traditional discrete FT [6] . Also, we can rewrite definition (2) as ![]() with
with ![]() and
and![]() , where
, where![]() ,
,![]() .
.
For DLCT, we have the following property [5] [6] :
![]() .
.
More details on DLCT can be found in [6] .
2.2. Frequency-Limiting Operators
Definition 1: Let ![]() be a complex-valued signal with
be a complex-valued signal with ![]() and its LCT
and its LCT![]() , if there is a function
, if there is a function ![]() vanishing outside
vanishing outside ![]() (
(![]() is a measurable set) such that
is a measurable set) such that![]() , then
, then ![]() is
is ![]() -concentrated.
-concentrated.
Specially, if![]() , then definition 1 reduces to the case in time domain [22] [23] . If
, then definition 1 reduces to the case in time domain [22] [23] . If![]() , then definition 1 reduces to the case in traditional frequency domain [22] [23] .
, then definition 1 reduces to the case in traditional frequency domain [22] [23] .
Definition 2: Generalized frequency-limiting operator ![]() is defined as
is defined as
![]() ,.
,.
If![]() , then definition 2 is the time-limiting operator [22] [23] . If
, then definition 2 is the time-limiting operator [22] [23] . If![]() , then definition 2 is the traditional frequency-limiting operator [22] [23] . Definitions 1 and 2 disclose the relation between
, then definition 2 is the traditional frequency-limiting operator [22] [23] . Definitions 1 and 2 disclose the relation between ![]() and
and![]() . For the discrete case, we have the following definitions.
. For the discrete case, we have the following definitions.
Definition 3: Let ![]()
![]() be a discrete sequence with
be a discrete sequence with ![]() and its DLCT
and its DLCT![]() , if there is a sequence
, if there is a sequence ![]() satisfying
satisfying ![]() such that
such that![]() , then
, then ![]() is
is ![]() -concentrated. Here,
-concentrated. Here, ![]() is the 0-norm operator that counts the non-zero elements.
is the 0-norm operator that counts the non-zero elements.
Definition 4: Generalized discrete frequency-limiting operator ![]() is defined as
is defined as
![]() with
with ![]() is the DLCT of
is the DLCT of ![]() and
and ![]() is the character function on
is the character function on![]() .
.
Clearly, definitions 3 and 4 are the discrete extensions of definitions 1 and 2. They have the similar physical meaning. These definitions are introduced for the first time, the traditional cases [22] [23] are only their special cases. Definition 3 and 4 disclose the relation between ![]() and
and![]() .
.
3. The Uncertainty Relations
3.1. The Uncertainty Principle
First let us introduce a lemma.
Lemma 3: ![]()
where ![]() is the Frobenius matrix norm.
is the Frobenius matrix norm.
Proof: From the definition of the operator ![]() in definition 4, we have
in definition 4, we have
![]() .
.
Exchange the locations of the sum operators, we obtain
![]()
Hence, according to the definition of the Frobenius matrix norm [1] and the definition of DLCT, we have
![]()
In the similar manner with the continuous case, we can obtain![]() . Since
. Since![]() , we have
, we have ![]() , thus, we get
, thus, we get ![]() . Therefore, we can obtain the following theorem 2.
. Therefore, we can obtain the following theorem 2.
Theorem 2: Let ![]()
![]() be the DLCT of the time sequence
be the DLCT of the time sequence ![]()
![]() for transform parameter
for transform parameter![]()
![]() , with
, with ![]()
![]()
![]()
![]() -concentrated on index set
-concentrated on index set ![]()
![]() . Let
. Let ![]()
![]() be the numbers of nonzero entries in
be the numbers of nonzero entries in ![]() (
(![]() respectively). Then
respectively). Then
![]() .
.
3.2. Extensions
Set ![]() in theorem 2, we can obtain the following theorem 3 directly.
in theorem 2, we can obtain the following theorem 3 directly.
Theorem 3: Let ![]()
![]() be the DLCT of the time sequence
be the DLCT of the time sequence ![]()
![]() with
with
length N. ![]()
![]() counts the numbers of nonzero entries in
counts the numbers of nonzero entries in ![]() (
(![]() respectively). Then
respectively). Then
![]()
Clearly, theorem 3 is a special case of theorem 2. Also, this theorem can be derived via theorem 1 in [25] .
Differently, we obtain this result in a different way. Here we note that since![]() , there is at least one non-zero element in every LCT domain for
, there is at least one non-zero element in every LCT domain for![]() . Therefore,
. Therefore, ![]() for
for![]() .
.
Through setting special value for ![]() in theorem 3, we have
in theorem 3, we have
Corollary 1: ![]() with
with![]() .
.
We can obtain the following more general uncertainty relation associated with DLCT.
Theorem 4: Let ![]()
![]() be the DLCT of the time sequence
be the DLCT of the time sequence ![]() (
(![]() and
and![]() ) with length
) with length ![]() and
and![]() .
. ![]() counts the number of nonzero elements in
counts the number of nonzero elements in![]() . Then
. Then
![]() with
with
Proof: From the assumption and the definition of DLCT [6] , we know
![]() for.
for.
where ![]()
![]() . Therefore, let
. Therefore, let![]() , have [25]
, have [25]
![]()
where ![]() and
and ![]() with
with ![]() and
and ![]() with
with![]() .
.
Hence, we obtain
![]()
Set![]() , then
, then
![]()
Using the triangle inequality, we have
![]()
hence
From ![]() and Parseval’s principle [6] , we obtain:
and Parseval’s principle [6] , we obtain:
![]() .
.
Hence
![]() .
.
Therefore, we obtain
![]()
Adding all the above inequalities, we have ![]() with
with![]() . Similarly, from
. Similarly, from ![]() and Parseval’s principle [6] , we obtain
and Parseval’s principle [6] , we obtain![]() , hence
, hence
![]() .
.
From the definition and property of DLCT [6] we have
![]()
with![]() .
.
Hence, we finally obtain ![]() with
with![]() . This theorem is the extension of theorem 3 and discloses the uncertainty relation between multiple signals.
. This theorem is the extension of theorem 3 and discloses the uncertainty relation between multiple signals.
4. Conclusion
In practice, for the discrete data, not only the supports are limited, but also they are sequences of data points whose number of non-zero elements is countable accurately. This paper discussed the generalized uncertainty relations on LCT in terms of data concentration. We show that the uncertainty bounds are related to the LCT parameters and the support lengths. These uncertainty relations will enrich the ensemble of uncertainty principles and yield the potential illumination for physics.
Acknowledgements
This work was fully supported by the NSFCs (61002052 and 61471412) and partly supported by the NSFC (61250006).
Supported
This work was fully supported by the NSFC (61002052) and partly supported by the NSFC (61250006 and 60975016).