1. Introduction
The scale symmetry in input (consumption) space embodied by homothetic production (utility) functions has long been recognized as a benchmark setting for the microeconomics of the producer (consumer). According to Chambers and Mitchell (2001) [1] , “Homotheticity may be the most common functional restriction employed in economics.” In fact, over the last two decades, substantial effort has been devoted to the generalization of homotheticity to multiple output production functions (see for instance the seminal contributions by Färe and Mitchell, 1993 [2] , Chambers and Färe, 1998 [3] , Chambers and Mitchell, 2001 [1] ).
In turn, input homothetic correspondences represent benchmark models in the input radial perspective on productive efficiency, for which Farrell (1957) [4] set forth a landmark approach: productive efficiency is decomposed into technical and allocative measures in a well defined order. Noticeably, in a recent contribution, Bogetoft et al. (2006) [5] generalize the Farrell approach, and fix the relevance of (input and input ray-) homotheticity for such a generalization (Mantovi, 2013 [6] addresses the corresponding problem for the consumer). It is the aim of the present short paper to apply such results, and thereby deepen the benchmark relevance of homotheticity, in terms of decompositions of the Lerner (1934) [7] index which parallel the decomposition set forth by Chambers et al. (2014) [8] .
The plan of the rest of the paper is as follows. In Section 2 we recall the decomposition set forth by Chambers et al. (2014) [8] . In Section 3 we set forth our decompositions. A final section envisages potential lines of progress.
2. Lerner Index and Economic Efficiency
In a seminal paper, Lerner (1934) [7] introduced the index 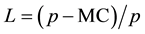 of monopoly power, lately resulted in a cornerstone of industrial economics. In a recent contribution, Chambers et al. (2014) [8] establish that the distance between L and 1 can be written as the product of the cost elasticity e, the Farrell output measure of technical efficiency
of monopoly power, lately resulted in a cornerstone of industrial economics. In a recent contribution, Chambers et al. (2014) [8] establish that the distance between L and 1 can be written as the product of the cost elasticity e, the Farrell output measure of technical efficiency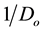 , and the reciprocal of what Georgescu-Roegen (1951) [9] called “return on the dollar”, i.e.
, and the reciprocal of what Georgescu-Roegen (1951) [9] called “return on the dollar”, i.e.
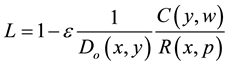 (1)
(1)
being p the price of the single output y, w the price vector for the input vector x, and C and R the cost and revenue functions respectively. Thus, the above measures of economic performance provide a sound factorization of fundamental determinants of market power. Noticeably, a key to such a decomposition is given by the identity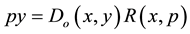 , which provides a handle to represent explicitly the inefficiency of production (an aspect which Lerner, 1934 [7] , does not seem to consider): once the output distance function
, which provides a handle to represent explicitly the inefficiency of production (an aspect which Lerner, 1934 [7] , does not seem to consider): once the output distance function
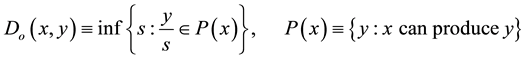 (2)
(2)
takes a value lower than 1, the input bundle x represents an inefficient production plan for the output level y, the lower Do the larger the inefficiency. Then, formula (1) fixes the effect of technical inefficiency on the Lerner index, as modulated by 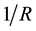 (being Do and R dual quantities). The index (1) is a function on the product of the (primal) technology set and the (dual) space of input and output prices; write X for such a space, domain of L.
(being Do and R dual quantities). The index (1) is a function on the product of the (primal) technology set and the (dual) space of input and output prices; write X for such a space, domain of L.
Noticeably, the Authors establish decomposition (1) in the context of an approach to the Lerner index as the first order derivative of the Nerlovian indicator, upon restricting to single output and fixing the radial perspective in input space (gx = 0 in the Nerlovian indicator). That being the case, homothetic production functions embody the well known properties resulting from input scale symmetry (straight expansion paths and separability of the cost function) which, in turn, fix a benchmark setting for the measurement of overall productive efficiency, as discussed in the following section.
3. Lerner Index and Overall Productive Efficiency
In a celebrated paper, Farrell (1957) [4] introduced a decomposition of overall productive efficiency as the product of technical efficiency and allocative efficiency. The relevance of such a decomposition has long been established; to the extent that technical and allocative efficiency represent a ‘natural’ pair, it is therefore natural to try and reshape the decomposition (1) along such lines.
In a recent article, Bogetoft et al. (2006) [5] challenge the univocity of Farrell decompositions. As is well known, standard Farrell decompositions entail assessing technical efficiency first, by projecting the actual input bundle x onto its correspondent 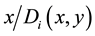 on the efficient frontier (being Di the input distance function), and then establishing allocative efficiency AE in ratio form as
on the efficient frontier (being Di the input distance function), and then establishing allocative efficiency AE in ratio form as
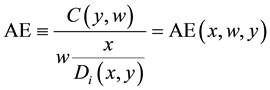 (3)
(3)
([5] , p. 453). That being the case, allocative efficiency “is treated as a residual” (ivi, p. 450). The standard justification for such an approach is that, on the one hand, allocative efficiency is well defined on the efficient frontier, whereas, on the other hand, it may not be well defined outside such a locus. Still, Bogetoft et al. (2006) [5] argue about the relevance of decomposing overall productive efficiency in the reversed order.
The authors define a “reverse Farrell approach”, in which allocative efficiency is established first, and technical efficiency is subsequently fixed by projecting the allocative efficient input bundle onto the efficient frontier. The authors themselves discuss several cases in which organizations may find it optimal to pursue allocative efficiency irrespective of, or at least prior to, technical efficiency; for instance, “it may be easier to reallocate resources within a hierarchy or via markets, than to actually change the production procedures” (ivi, p. 451).
Thus, Bogetoft et al. (2006) [5] define reversed allocative efficiency, with respect to a reference output level 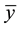 (which identifies an isoquant through x) as
(which identifies an isoquant through x) as
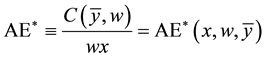 (4)
(4)
and reversed technical efficiency subsequently, and then prove that standard and reversed Farrell decompositions do coincide for (input and input ray-) homothetic technologies. Correspondingly, exploiting the well known isomorphism between the microeconomic problems of the producer and of the consumer, Mantovi (2013) [6] tailors a parallel between such a result and the commutativity of suitably defined finite expansion and substitution effects (recall, the infinitesimal expansion and substitution effects represented in Slutsky decompositions do commute by definition) in terms of the flows of vector fields on consumption space, with the generator of homotheties playing the key role (Tyson, 2013 [10] employs vector fields on consumption space in order to characterize the symmetries of preferences).
How about the consistency of employing the above measures of allocative efficiency in order to reshape the decomposition (1)? True, the technical efficiency measure employed by Chambers et al. (2014) [8] does not coincide with the one employed by Bogetoft et al. (2006) [5] (for instance, constant returns to scale imply that the input and output distance functions are reciprocal, see for instance Chambers et al. (1998) [11] ); let us align with the definition of TE and TE* in [5] , in order to envision the relevance of standard and reversed Farrell decompositions applied to L.
As expected, no problem arises for standard Farrell decompositions: via definition (3) the decomposition (1) can be written
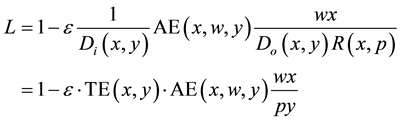 (5)
(5)
in which we factorize the effects of the overall efficiency TE×AE and of the expenditure/revenue ratio wx/py.
Consider then the reversed measures AE*, TE*: following Bogetoft et al. (2006) [5] , one can multiply both
sides of the Chambers-Färe-Grosskopf decomposition (1) by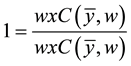 , and employ definition (4) to write
, and employ definition (4) to write
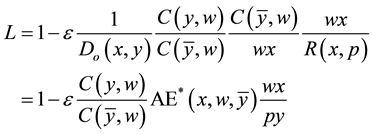 (6)
(6)
with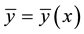 . Then, capitalizing on the results in [5] , we readily establish that we can interpret
. Then, capitalizing on the results in [5] , we readily establish that we can interpret 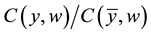 as the measure TE* of technical efficiency if and only if the production function is homothetic (as is well known, that being the case, the cost function can be written as the product of a function of w and a function of y, and therefore the ratio
as the measure TE* of technical efficiency if and only if the production function is homothetic (as is well known, that being the case, the cost function can be written as the product of a function of w and a function of y, and therefore the ratio 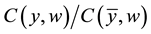 does not depend on w).
does not depend on w).
4. Conclusions
To sum up, overall productive efficiency seems to tailor pregnant parallels to the Chambers-Färe-Grosskopf decomposition of the Lerner index as a function L on X. On conceptual grounds, such a function establishes a fundamental link between production analysis and industrial economics; on analytical grounds, the full range of variables (both primal and dual) which span X enables us in principle to employ the full theory of duality in order to express L in terms of the relevant quantities. In such respects, our expressions (5) and (6) of L establish a connection with the celebrated Farrell decomposition of overall productive efficiency, and in fact with the interesting advances set forth by Bogetoft et al. (2006) [5] , in which the order does matter with which (input) technical efficiency is computed with respect to allocative efficiency, unless the scale symmetry of the problem guarantees the commutativity of expanding along rays and sliding along isoquants. We thereby envision one more instance of the benchmark relevance of homothetic models. Chambers et al. (2014) [8] envision the generalization of their decomposition to multiple output as a natural line of progress. In the author’s view, such a perspective may prove relevant for our decompositions as well, on account of the ongoing progresses in the analysis of homotheticity (see for instance Zelenyuk, 2014 [12] and references therein).
Still, the single output case may prove quite interesting for deepening the properties of nonhomothetic models. In such respects, Mantovi (2013) [6] tailors a differential geometric approach to the commutativity of (suitably defined) expansion and substitution effects, which are isomorphic to technical and allocative (in)efficiency measures for a single output production function, in terms of Lie brackets. Such a geometric approach to overall productive efficiency (and its reflection on the Lerner index) may shed light on the “second order” allocative inefficiency defined by Bogetoft et al. (2006) [5] , and, in turn, on the dynamics of efficient input allocations (see for instance Choi et al., 2006 [13] and references therein) and construction of index numbers (Cross and Färe, 2015 [14] assume homotheticity in their construction of the Fisher index). In addition, a connection may emerge with the path dependence of Divisia indices for non-homothetic problems (Samuelson and Swamy, 1974) [15] ; notice for instance that if the time rates of change of individual inputs do coincide, the factor wx/py
emerges in the definition ![]() of the time rate of change of the aggregate input index (Chambers, 1988
of the time rate of change of the aggregate input index (Chambers, 1988
[16] , p. 238).