Existence of Viscosity Solutions to a Parabolic Inhomogeneous Equation Associated with Infinity Laplacian ()
1. Introduction
In this paper, we consider the nonlinear degenerate parabolic inhomogeneous equation involving infinity La- place
 , (1)
, (1)
where
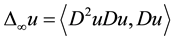
denotes the 3-homogeneous infinity Laplacian. We want to establish the existence result of viscosity solutions to the initial and Dirichlet boundary problem.
The homogeneous infinity Laplace equation 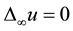 is the Euler-Lagrange equation associated with
is the Euler-Lagrange equation associated with  - variational problem. See for details [1] -[5] and the references therein. Recently, Juutinen and Kawohl [6] con- sidered the degenerate and singular parabolic equation
- variational problem. See for details [1] -[5] and the references therein. Recently, Juutinen and Kawohl [6] con- sidered the degenerate and singular parabolic equation
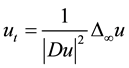 . (2)
. (2)
They proved the existence and uniqueness for both Dirichlet and Cauchy problems, established interior and boundary Lipschitz estimates and a Harnack inequality, and also provided numerous explicit solutions. Due to the degeneracy and the singularity of the Equation (2), they introduced the approximating equations to obtain the existence result with the aid of the uniform continuity estimates. And in [7] we considered the corresponding inhomogeneous parabolic equation. Notice that the 1-homogeneous infinity Laplacian
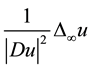 (3)
(3)
is related to game theory named tug-of-war [8] . In [9] -[12] , Akagi, Suzuki, et al. considered the following degenerate parabolic equation
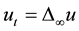 .
.
They also introduced the corresponding approximating equations and got the uniform continuity estimates of approximate solutions by the barrier function arguments. By this approximate procedure, the existence of the solutions was obtained. They also proved the uniqueness and the asymptotic behavior of the viscosity solutions. In [13] , Portilheiro and Vázquez considered the parabolic equation
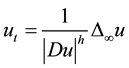 ,
,
with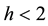 . They proved existence and uniqueness of viscosity solutions and derived the asymptotic behavior of the solutions for the Cauchy problem and the initial and Dirichlet problem with zero boundary conditions. In [14] , Portilheiro and Vázquez studied the nonlinear porous medium type equation involving the infinity Laplacian operator
. They proved existence and uniqueness of viscosity solutions and derived the asymptotic behavior of the solutions for the Cauchy problem and the initial and Dirichlet problem with zero boundary conditions. In [14] , Portilheiro and Vázquez studied the nonlinear porous medium type equation involving the infinity Laplacian operator
 . (4)
. (4)
By the density-to-pressure transformation, they transformed the Equation (4) into a new equation, then the existence, uniqueness and asymptotic behavior etc. were obtained.
In this article, we are interested in the parabolic version of the infinity Laplacian here. We think that Equation (1) is interesting, because it not only is degenerate, but also has many applications in image processing and optimal transportation etc. The parabolic equation involving infinity Laplacian operator has received a lot of attention in the last decade, notably due to its application to image processing, the main usage being in the reconstructions of damaged digital images [15] . For numerical purposes it has been necessary to consider also the evolution equation corresponding to the infinity Laplace operator. We prove the existence of viscosity solu- tions to the initial-Dirichlet problem by approximating procedure. The approximation process is introduced in [6] for the infinity Laplacian evolution and followed in [9] [13] [14] etc.
This paper is organized in the following order. In Section 2, we give the notations, definitions of viscosity solutions related to the Equation (1). In Section 3, we prove our main existence result by approximating pro- cedure.
2. Preliminaries
Throughout of this paper, we use the following notation: If ,
, 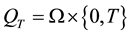 ,
, 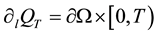 denotes the lateral bouncary,
denotes the lateral bouncary, ![]() the bottom boundary, and
the bottom boundary, and ![]() (the para- bolic boundary of
(the para- bolic boundary of![]() ).
). ![]() and
and ![]() denote the largest and the smallest of the eigenvalues to a symmetric matrix.
denote the largest and the smallest of the eigenvalues to a symmetric matrix. ![]() denotes those functions which are twice differentiable in
denotes those functions which are twice differentiable in ![]() and once in
and once in![]() .
.
In the following paper, we adopt the definition of viscosity solutions, (see for example [16] ).
Definition 2.1. Suppose that ![]() is upper semi-continuous. If for every
is upper semi-continuous. If for every ![]() and
and ![]() test function
test function ![]() such that
such that ![]() has a strict local maximum at point
has a strict local maximum at point![]() , that is
, that is ![]() and
and ![]() in a neighborhood of
in a neighborhood of![]() , there holds
, there holds
![]() , (5)
, (5)
then we say that ![]() is a viscosity sub-solution of (1).
is a viscosity sub-solution of (1).
Similarly, ![]() is lower semi-continuous. If for every
is lower semi-continuous. If for every ![]() and
and ![]() test function
test function ![]() such that
such that ![]() has a strict local minimum at point
has a strict local minimum at point![]() , there holds
, there holds
![]()
then we say that ![]() is a viscosity super-solution of (1).
is a viscosity super-solution of (1).
If ![]() is both a viscosity sub-solution and a viscosity super-solution, then we say that
is both a viscosity sub-solution and a viscosity super-solution, then we say that ![]() is a vis- cosity solution of (1).
is a vis- cosity solution of (1).
3. Existence Theorem
In this section we will prove the existence of viscosity solutions to (1) with the initial and boundary data![]() . The method we adopt is the approximation procedure introduced in [6] and used in [9] [13] [14] etc. The main existence result we obtain is.
. The method we adopt is the approximation procedure introduced in [6] and used in [9] [13] [14] etc. The main existence result we obtain is.
Theorem 3.1. Let![]() , where
, where ![]() is a bounded domain,
is a bounded domain, ![]() is continuous in
is continuous in![]() , and let
, and let![]() . Then there exists a function
. Then there exists a function ![]() such that
such that ![]() on
on ![]() and
and
![]() (6)
(6)
in ![]() in the viscosity sense.
in the viscosity sense.
We use the approximate procedure, cf, [6] [9] [14] . We consider the approximating equations
![]() , (7)
, (7)
where
![]() (8)
(8)
with![]() . For this equation with smooth initial and boundary data
. For this equation with smooth initial and boundary data![]() , the existence of a smooth solution
, the existence of a smooth solution ![]() is guaranteed by classical results in [17] . Our goal is to obtain a solution of (1) as a limit of these functions as
is guaranteed by classical results in [17] . Our goal is to obtain a solution of (1) as a limit of these functions as![]() . This amounts to proving uniform estimates for
. This amounts to proving uniform estimates for ![]() that are independent of
that are independent of![]() . The estimates we require will be obtained by using the standard barrier method.
. The estimates we require will be obtained by using the standard barrier method.
Theorem 3.2. (Boundary regularity at![]() ) Let
) Let![]() , where
, where ![]() is a bounded domain,
is a bounded domain, ![]() is continuous in
is continuous in![]() , and let
, and let![]() . Suppose that
. Suppose that ![]() is a smooth solution satisfying
is a smooth solution satisfying
![]()
Then there exists a constant ![]() depending on
depending on![]() ,
, ![]() and
and ![]() but independent of
but independent of ![]() such that
such that
![]() .
.
Moreover, if ![]() is only continuous in
is only continuous in ![]() (possibly discontinuous in
(possibly discontinuous in![]() ) and bounded in
) and bounded in![]() , then the modulus of continuity of
, then the modulus of continuity of ![]() on
on ![]() (for small
(for small![]() ) can be estimated in terms of
) can be estimated in terms of![]() ,
, ![]() and the modulus of continuity of
and the modulus of continuity of ![]() in
in![]() .
.
Proof. Step 1. Suppose first that ![]() and we consider the upper barrier function
and we consider the upper barrier function
![]() ,
,
where ![]() is to be determined. We have
is to be determined. We have
![]()
if![]() . Therefore
. Therefore ![]() is a super-solution.
is a super-solution.
Clearly, ![]() for all
for all![]() . Moreover, for
. Moreover, for ![]() and
and![]() ,
,
![]() ,
,
if![]() , That is,
, That is, ![]() on
on![]() .
.
Thus, by the classical comparison principle, we obtain
![]()
for every![]() . Similarly, by considering also the lower barrier function
. Similarly, by considering also the lower barrier function
![]() ,
,
we obtain the symmetric inequality, and hence the Lipschitz estimate
![]() (9)
(9)
for ![]() and
and
![]() .
.
Step 2. Suppose now that ![]() is only continuous in
is only continuous in ![]() and let
and let ![]() be its modulus of continuity. Let us fix
be its modulus of continuity. Let us fix
a point ![]() and
and![]() . Let us consider the smooth functions
. Let us consider the smooth functions
![]() .
.
It is easy to check that ![]() on the parabolic boundary
on the parabolic boundary![]() .
.
Thus if ![]() are the unique classical solutions to (7) with boundary and initial data
are the unique classical solutions to (7) with boundary and initial data![]() , respectively, we have
, respectively, we have ![]() in
in ![]() by the classical comparison principle again. Since
by the classical comparison principle again. Since ![]() are smooth, we can use estimate (9) to conclude that
are smooth, we can use estimate (9) to conclude that
![]() ,
,
where ![]() depends on
depends on![]() ,
, ![]() and
and![]() . Therefore,
. Therefore,
![]()
with this inequality it is straightforward to complete the proof. □
The full Lipschitz estimate in time now follows easily with the aid of the comparison principle and the fact that the Equation (7) is translation invariant.
Corollary 3.3. (Lipschitz regularity in time) If ![]() is continuous in
is continuous in![]() ,
, ![]() and
and ![]() is as in
is as in
Theorem 3.2, then there exists a constant ![]() depending on
depending on![]() ,
, ![]() and
and ![]() but independent of
but independent of
![]() such that
such that
![]()
for all ![]() and
and![]() . Moreover, if
. Moreover, if ![]() is only continuous, then the modulus of continuity of
is only continuous, then the modulus of continuity of ![]() on
on ![]() can be estimated in terms of
can be estimated in terms of![]() ,
, ![]() and the modulus of continuity of
and the modulus of continuity of![]() .
.
Proof. Let![]() ,
,![]() . Then both u and ũ are smooth solutions to (7) in
. Then both u and ũ are smooth solutions to (7) in![]() ,
,
and hence if![]() , we have
, we have
![]()
by the classical comparison principle and Theorem 3.2. This implies the Lipschitz estimate asserted above, and the proof for the case when ![]() is only continuous is analogous. □
is only continuous is analogous. □
Theorem 3.4. (Hölder regularity at the lateral boundary) Let![]() , where
, where ![]() is a bounded domain,
is a bounded domain, ![]() is continuous in
is continuous in![]() , and let
, and let![]() . Suppose that
. Suppose that ![]() is a smooth solution satisfying
is a smooth solution satisfying
![]()
Then for each![]() , there exists a constant
, there exists a constant ![]() depending on
depending on![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() but independent of
but independent of ![]() and
and ![]() sufficiently small such that
sufficiently small such that
![]() ,
,
for all ![]() and
and![]() .
.
Proof. Step 1. For every ![]() and
and![]() , let
, let
![]() ,
,
where![]() ,
, ![]() are to be determined. Then a straightforward computation gives
are to be determined. Then a straightforward computation gives
![]()
If ![]() and
and![]() , we have
, we have
![]() .
.
Therefore
![]() ,
,
if![]() .
.
We have shown that ![]() is a super-solution of (7).
is a super-solution of (7).
Step 2. Let![]() , where
, where![]() . We want to prove first
. We want to prove first ![]() on
on![]() . Case 1. If
. Case 1. If![]() , then
, then
![]()
provided ![]() and
and![]() .
.
Case 2. If![]() , it is easy to see that
, it is easy to see that ![]() is a super-solution of (7) in
is a super-solution of (7) in ![]() and
and ![]() on
on![]() . Hence, we have
. Hence, we have
![]()
provided![]() , and in the last inequality we have used the comparison principle.
, and in the last inequality we have used the comparison principle.
Step 3. To prove ![]() on
on![]() .
.
Case 1. If![]() , then
, then![]() , and notice that since
, and notice that since ![]() on the bottom of this cylinder,
on the bottom of this cylinder,
![]()
if ![]() and
and![]() .
.
Case 2. If![]() , then
, then![]() . Using the comparison principle again, we have
. Using the comparison principle again, we have
![]()
if![]() .
.
Step 4. In conclusion, we have shown that ![]() on
on![]() , if we choose
, if we choose
![]() ,
,
![]() .
.
Therefore, we have ![]() in
in ![]() by the comparison principle. In particular,
by the comparison principle. In particular,
![]()
for![]() . Using the lower barrier
. Using the lower barrier
![]() ,
,
we get the symmetric inequality. This finishes the proof. □
Due to the translation invariant of the equation and the comparison principle, we can extend the Hölder estimate to the interior of the domain, cf. [6] [14] etc.
Corollary 3.5. (Hölder regularity in space) Let![]() , where
, where ![]() is a bounded domain,
is a bounded domain, ![]() is continuous in
is continuous in![]() , and let
, and let![]() . Suppose that
. Suppose that ![]() a smooth solution satisfying
a smooth solution satisfying
![]()
Then there exists![]() , and constants
, and constants![]() , depending on
, depending on ![]()
![]() ,
, ![]() ,
, ![]() and
and ![]() but independent of
but independent of ![]() and
and ![]() sufficiently small such that
sufficiently small such that
![]() ,
,
for all![]() .
.
Proof. Step 1. For fixed![]() , take a point
, take a point ![]() and let
and let![]() . Define
. Define![]() .
.
By Theorem 3.4 we have that ![]() on
on ![]() (noting that in this case
(noting that in this case ![]() or
or
![]() ). Hence
). Hence ![]() for every
for every ![]() by the comparison principle. This means that whenever
by the comparison principle. This means that whenever ![]() or
or ![]() with
with![]() , we have
, we have![]() .
.
Step 2. When![]() , using the comparison principle we get
, using the comparison principle we get
![]() .
.
This finishes the proof. □
The following theorem shows that one can obtain the Lipschitz estimate when one remove the Laplacian term from the equation, cf. [6] .
Theorem 3.1 follows now easily from Theorem 3.2 and 3.3 and the stability properties of viscosity solutions.
Proof. (Proof of Theorem 3.1) If ![]() and
and ![]() is the unique smooth solution to
is the unique smooth solution to
![]()
Corollaries 3.3 and 3.5 and the comparison principle imply that the family of functions ![]() is equicon- tinuous and uniformly bounded. Therefore, up to a subsequence,
is equicon- tinuous and uniformly bounded. Therefore, up to a subsequence, ![]() as
as ![]() and
and ![]() is the unique viscosity solution to (7) by the stability properties of viscosity solutions.
is the unique viscosity solution to (7) by the stability properties of viscosity solutions.
The existence for a general continuous data ![]() follows by approximating the data by smooth functions and using Corollaries 3.3 and 3.5 and the stability properties of viscosity solutions again. □
follows by approximating the data by smooth functions and using Corollaries 3.3 and 3.5 and the stability properties of viscosity solutions again. □
Acknowledgements
The author would like to thank the anonymous referee for some valuable suggestions.
Support
This work is supported by the National Natural Science Foundation of China, No.11171153.