Some New Delay Integral Inequalities Based on Modified Riemann-Liouville Fractional Derivative and Their Applications

Zhimin Zhao, Run Xu^*

Department of Mathematics, Qufu Normal University, Qufu, China.

DOI: 10.4236/jamp.2015.35059                

Abstract

By using the properties of modified Riemann-Liouville fractional derivative, some new delay integral inequalities have been studied. First, we offered explicit bounds for the unknown functions, then we applied the results to the research concerning the boundness, uniqueness and continuous dependence on the initial for solutions to certain fractional differential equations.

Keywords

Modified, Riemann-Liouville, Fractional Derivative, Integral Inequalities, Delay Fractional Differential Equation

1. Introduction

The common differential and integral inequalities are playing an important role in the qualitative analysis of differential equations. At the same time, delay integral and differential inequality have been studied due to their wide applications [1] -[3] . In recent years, the fractional differential and fractional integrals are adopted in var- ious fields of science and engineering. In addition, the fractional differential inequalities have also been studied [4] -[10] . We also need to study the delay differential equation and delay differential inequalities when dealing with certain problems. However, to the best of our knowledge, very little is known regarding this problem [11] . In this paper, we will investigate some delay integral inequalities.

In 2008, Zhiling Yuan, et al. [3] studied the following form delay integral inequality

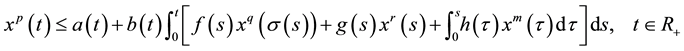(1)

then they offered an explicit estimate for, and applied this result to research the properties of solution to certain differential equations.

In 2013, Bin Zheng and Qinghua Feng [6] put forward the following form of fractional integral inequality

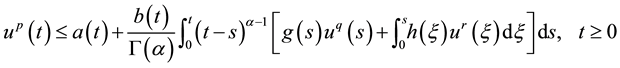, (2)

and they applied the obtained results to study the properties of solution.

In this paper, combining (1) and (2), we will explore the following form of delay integral inequality

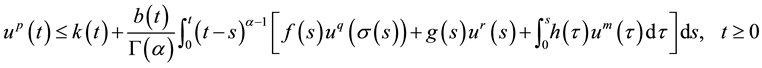. (3)

Now we list some Definitions and Lemmas which can be used in this paper.

Definition 1. [6] The modified Riemann-Liouville derivative of order 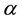is defined by

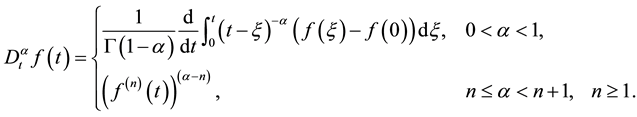
Definition 2. [6] The Riemann-Liouville fractional integral of order 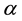on the interval 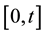is defined by

.

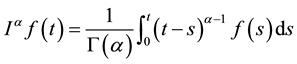Some important properties for the modified Riemann-Liouville derivative and fractional integral are listed as follows [6] (the interval concerned below is always defined by).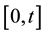

(1),

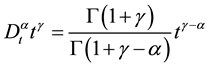(2),

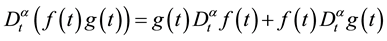(3),

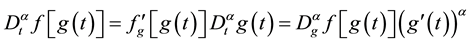(4),

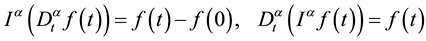(5).

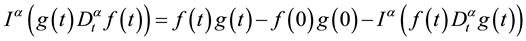Lemma 1. [3] Assume that, , and, then

.

Lemma 2. [6] Let, , , be continuous functions defined on.

Then for,

Implies

.

2. Main Results

Theorem 1 Assume that, , , , , , , and, are nondecreasing functions in. If satisfies the following form of delay integral inequality

, (4)

with the initial condition

,

(5)

where, , , , , , , are constants, , ,

and, then we have

(6)

for any, where

Proof. Fix, let

, (7)

,

Since, , , , , , , there’s exist a constant, such that

,

and is convergence integral,

so we have

we have is a nonnegative and nondecreasing. From (4) and (7) we get

, (8)

and

. (9)

So for with, we have

, (10)

for with, we have

. (11)

Combining (10) and (11), we obtain

, (12)

From (8), (9) and (12) we get

, (13)

By Lemma 1 we have

(14)

Since, , are continuous and there exists a constant satisfies

for, where. Then we get

,

so we have

, (15)

Using Lemma 2 to (14) we get

(16)

Letting in (16) and considering is arbitary, after substituting with, we get

(17)

Combining (8) and (17), we get (6).

Remark 1. Assume, then the inequalities in Theorem 1 reduce to Lemma 5 in [6] .

Theorem 2. Assume that, , , , , , , are defined as in Theorem 1. If satisfies the following form of integral inequality,

, (18)

where, , , are constants and satisfy

, (19)

with the condition (5) in Theorem 1, then we have

, (20)

where

.

Proof. Let

, (21)

Since are nonegative functions, is also nonegative and nondecreasing func- tion, in addition, there exists a constant satisfying

for, where. Then we get

,

so we can get. From (18) we have

, (22)

and

. (23)

By Lemma 1 we get for any,

. (24)

Proceeding the similar proof of Theorem 3 in [3] , we can get

. (25)

From (23), (24), (25) and condition (19) we have

(26)

By Lemma 2 we have

. (27)

Combining (22) and (27), (20) can be obtained subsequently.

Theorem 3. Assume that, , , , , and is nondecreasing with for. If satisfies

, (28)

then

, (29)

where

.

Proof. Let

,

then we get

. (30)

Since are both continuous functions, is continuous and there exists a con-

stant satisfying for, where. Then we get

,

so we get and

By Lemma 2 we have

. (31)

Combining (30) and (31), we get (29).

Remark 2. Considering in Theorem 3, proceeding the similar proof of Theorem 3, we can get

.

Theorem 4. Assume that, , , , and is nonde- creasing with for, with. If satisfies the following form of delay integral inequality

, (32)

then

, (33)

where

,

.

Proof. Let

,

then we get

, (34)

The assumptions on and imply that is nondecreasing and there exists a constant

satisfying for, where.

Then we get

,

so we have. For, we have

,

and

(35)

Using Lemma 4 to (35), we can get

. (36)

Combining (34) and (36), we get (33).

Remark 3. Considering and in Theorem 4, we can get Remark 2.

3. Applications

In this section, we will show that the inequalities established above are useful in the research concerning the boundness, uniqueness and continuous dependence on the initial value for solutions to fractional differential equations.

3.1. Consider the Following Fractional Differential Equation

,

. (37)

with the condition

,

, (38)

where, is a constant, , , ,

And

,

Example 1. Assume that satisfies

, (39)

where are nonnegative continuous functions on, then we have the following estimate for,

(40)

where

.

Proof. By Equation (37), we have

. (41)

By (39) and (41) we can get

(42)

With a suitable application of Theorems 1 to (42) (with, , , ,), we can obtain the desired result. This complete the proof of Example 1.

Example 2. Assume that

, (43)

where are nonnegative continuous functions defined, is the quotient of two odd num- bers. Equation (37) has a unique solution.

Proof. Suppose are two solutions of Equation (37), then we have

Furthermore,

which implies

(44)

Through a suitable application of Theorem 1 to (44) (with, ,), we can obtain

,

which implies. So Equation (37) has a unique solution.

Example 3. Suppose that is the solution of (37) and be the solution of the following fractional integral equation,

,

. (45)

If satisfies the condition (43), then the solution of Equation (37) depends on the initial value continuously.

Proof. By Equation (45), we have

, (46)

so we get

Furthermore

(47)

Apply Theorem 1 to (47) (with, , ,), we get

,

where. This gives that the solutions of Equation (37) depends on the initial value continuously.

3.2. Consider the Following Fractional Differential Equation

,

. (48)

Example 4. Assume that is a solution of Equation (48), then is bounded.

Proof. By Equation (48) we can get

. (49)

with a suitable application of Theorem 3 to (49) (with, , , , for, ,), we have

where we used. This complete the proof of Example 4.

Example 5. If is a solution of (48), then it has a unique solution.

Proof. Suppose are two solutions of Equation (48), then we have

Furthermore,

,

which implies

. (50)

With a suitable application of 3 to (50) (with, , , , , for), we can obtain

,

which implies. So Equation (48) has a unique solution.

Example 6. Suppose that is the solution of (48) and is the solution of the following fractional integral equation,

,

. (51)

Then all the solutions of Equation (48) depend on the initial value continuously.

Proof. By Equation (51), we have

,

so we get

Furthermore

. (52)

Apply Theorem 3 to (52) (with, , , , for,

,), we get

(53)

where we use the fact that

This gives that depends on the initial value continuously.

Acknowledgements

We thank the Editor and the referee for their comments. This work is supported by National Science Foundation of China (11171178 and 11271225).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Jiang, F.C. and Meng, F.W. (2007) Explicit Bounds on Some New Nonlinear Integral Inequalities with Delay. Journal of Computational and Applied Mathematics, 205, 479-486. http://dx.doi.org/10.1016/j.cam.2006.05.038
[2]	Zhang, H.X. and Meng, F.W. (2008) Integral Inequalities in Two Independent Variables for Retarded Volterra Equations. Applied Mathematics and Computation, 199, 90-98. http://dx.doi.org/10.1016/j.amc.2007.09.026
[3]	Yuan, Z.L., Yuan, X.W., Meng, F.W. and Zhang, H.X. (2008) Some New Delay Integral Inequalities and Their Applications. Journal of Computational and Applied Mathematics, 180, 191-200.
[4]	Zheng, B. (2013) Some New Gronwall-Bellman-Type Inequalities Based on the Modified Riemann-Liouville Fractional Derivative. Hindawi Publishing Corporation Journal of Applied Mathematics, 2013, Article ID: 341706. http://dx.doi.org/10.1155/2013/341706
[5]	Zheng, B. (2014) Explicit Bounds Derived by Some New Inequalities and Applications in Fractional Integral Equations. Journal of Inequalities and Applications, 2014, 4. http://www.journalofinequalitiesandapplications.com/content/2014/1/4 http://dx.doi.org/10.1186/1029-242X-2014-4
[6]	Zheng, B. and Feng, Q.H. (2013) New Gronwall-Bellman Type Inequalities and Applications in the Analysis for Solutions to Fractional Differential Equations. Hindawi Publishing Corporation Abstract and Applied Analysis, 2013, Article ID: 705126. http://dx.doi.org/10.1155/2013/705126
[7]	Denton, Z. and Vatsala, A.S. (2010) Fractional Integral Inequalities and Applications. Computers and Mathematics with Applications, 59, 1087-1094. http://dx.doi.org/10.1016/j.camwa.2009.05.012
[8]	Ye, H.P., Gao, J.M. and Ding, Y.S. (2007) A Generalized Gronwall Inequality and Its Application to a Fractional Differential Equation. Journal of Mathematical Analysis and Applications, 328, 1075-1081. http://dx.doi.org/10.1016/j.jmaa.2006.05.061
[9]	Khalil, R., Al Horani, M., Yousef, A. and Sababheh, M. (2014) A New Definition of Fractional Derivative. Journal of Computational and Applied Mathematics, 264, 65-70. http://dx.doi.org/10.1016/j.cam.2014.01.002
[10]	Jessada, T., Ntouyas, S.K. and Weerawat, S. (2014) Some New Riemann-Liouville Fractional Integral Inequalities. Hindawi Publishing Corporation International Journal of Mathematics and Mathematical Sciences, 2014, Article ID: 869434. http://dx.doi.org/10.1155/2014/869434
[11]	Jalilian, Y. and Jalilian, R. (2013) Existence of Solution for Delay Fractional Differential Equations. Mediterranean Journal of Mathematics, 10, 1731-1747.