Numerical Solution of Green’s Function for Solving Inhomogeneous Boundary Value Problems with Trigonometric Functions by New Technique ()
1. Introduction
In mathematics, a Green’s function is the impulse response of an inhomogeneous differential equation defined on a domain, with specified initial conditions or boundary conditions. Via the superposition principle, the con- volution of a Green’s function with an arbitrary function 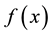 on that domain is the solution to the inhomo- geneous differential equation for
on that domain is the solution to the inhomo- geneous differential equation for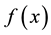 . Green’s functions were named after the British mathematician George Green, who first developed the concept in the 1830s. Under many-body theory, the term is also used in physics, specifically in quantum field theory, aerodynamics, aeroacoustics, electrodynamics and statistical field theory, to refer to various types of correlation functions, even those that do not fit the mathematical definition.
. Green’s functions were named after the British mathematician George Green, who first developed the concept in the 1830s. Under many-body theory, the term is also used in physics, specifically in quantum field theory, aerodynamics, aeroacoustics, electrodynamics and statistical field theory, to refer to various types of correlation functions, even those that do not fit the mathematical definition.
For concreteness, we assume that all functions are defined on the interval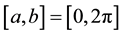 , and we consider second-order ordinary differential operators
, and we consider second-order ordinary differential operators  of the form
of the form
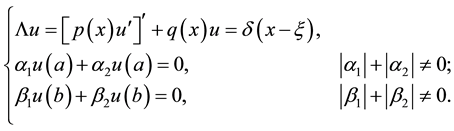 (1)
(1)
where functions 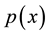 and
and 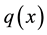 are cntinuous for
are cntinuous for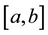 , and
, and 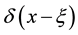 is dirac delta function. We look for a solution of 1 in the form
is dirac delta function. We look for a solution of 1 in the form
 (2)
(2)
where 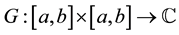 is a suitable function, called the Green’s function of 1.
is a suitable function, called the Green’s function of 1.
In most situations, it is difficult to obtain exact solution of the above integration. Hence, various approxi- mation methods have been proposed and studied. The purpose of the present paper is to develop a trigonometric Hermite wavelet approximation for the computing the Green’s function of the problem 2.
Recently, the arisen wavelet Galerkin method has demonstrated its advantages for the treatment of integral operators [1] -[5] . It is discovered in [6] that wavelet represents the singular integral operator. The development of fast methods for integral equations opens new perspectives. The methods like the fast multipole method [7] and the panel clusteing [8] reduce the complexity largely. A difficulty of using wavelet for the representation of integral operators is that quadrature leads to potentially high cost with sparse matrix. This fact particularly en- courages us in efforts to devote to some appropriate wavelet bases to simplify the computation expense of the reoresentation matrix, which is importent to improve the wavelet method. Nowadays, the trigonometric inter- polant wavelet has arisen in the approximation of operators [9] - [11] . Quack [12] has constructed a multire- solution analysis (MRA) of nested subspace of trigonometric Hermite polynomials. The trigonometric Hermite interpolation enables a completely explicit description of the corresponding decomposition and reconstruction coefficients by means of some circular matrices. Chen [13] [14] presented the feasibility of trigonometric wave- let numerical methods for stokes problem and Hadamard integral equation.
The outline of this paper is as follows. In Section 2, we describe the trigonometric scaling function on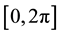 , and in Section 3 we construct the operational matrix of derivative for these function. In Section 4, the proposed method is used to approximate the solution of the problem. As a result, a problem of integration of a matrix is obtained, where by calculating the Green’s function of this matrix we get to the solution of the problem. In Section 5, we report our computational results and demonstrate the accuracy of the proposed numerical schemes by presenting numerical examples. Section 6 ends this paper with a brief conclusion.
, and in Section 3 we construct the operational matrix of derivative for these function. In Section 4, the proposed method is used to approximate the solution of the problem. As a result, a problem of integration of a matrix is obtained, where by calculating the Green’s function of this matrix we get to the solution of the problem. In Section 5, we report our computational results and demonstrate the accuracy of the proposed numerical schemes by presenting numerical examples. Section 6 ends this paper with a brief conclusion.
2. Trigonometric Scaling Function on 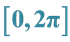
In this section, we will give a brief introduction of Quak’s work on the construction of Hermite interpolatory trigonometric wavelets and their basic properties (see [12] ). For all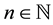 , the Dirichlet kernel
, the Dirichlet kernel 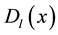 and its conjugate kernel
and its conjugate kernel ![]() are defined as
are defined as
![]()
Obviously, ![]() is the linear space of trigonometric polynomials with degree not exceeding l.
is the linear space of trigonometric polynomials with degree not exceeding l.
The equally spaced nodes on the interval ![]() with a dyadic step are denoted by
with a dyadic step are denoted by![]() , for any
, for any
![]() , and
, and![]() , where
, where![]() ,
, ![]() is the set of all non-negative integers.
is the set of all non-negative integers.
Definition 1 (Scaling functions). (See [12] .) For all![]() , the scaling functions
, the scaling functions![]() ,
, ![]() where
where ![]() for
for ![]() and
and ![]() are defined as
are defined as
![]()
Lemma 1 (See [12] .) For![]() , we have
, we have
![]()
and their derivations are given by
![]()
Theorem 2 (Interpolatory properties of the scaling functions). (See [12] .) For![]() , The following inter- polatory properties hold for each
, The following inter- polatory properties hold for each ![]()
![]() , (3)
, (3)
![]() . (4)
. (4)
From above we can take wavelet functions![]() ,
, ![]() ,
, ![]() as scaling functions. Then we have
as scaling functions. Then we have
Definition 3 (Scaling functions space). For all ![]() define the wave space
define the wave space ![]() as follows
as follows
![]()
As a first step of studying the spaces![]() , the following result identifies the trigonometric polynomials which from alternative bases of these spaces.
, the following result identifies the trigonometric polynomials which from alternative bases of these spaces.
Theorem 4 For any![]() , we have
, we have
![]()
consequently![]() .
.
Definition 5 For any![]() , the interpolation operator
, the interpolation operator ![]() mapping any real valued differentiable
mapping any real valued differentiable ![]() - periodic function
- periodic function ![]() into the space
into the space ![]() is defined as
is defined as
![]() (5)
(5)
where ![]()
![]() , and C and
, and C and ![]() are vectors with dimension
are vectors with dimension![]() .
.
The following properties of the operators ![]() are therefore obvious:
are therefore obvious:
![]()
![]()
![]() .
.
Theorem 6 Let![]() , and its trigonometric wavelet approximation is
, and its trigonometric wavelet approximation is![]() , then we have
, then we have
![]()
where C is a positive constant value.
Proof. See [12] .
3. The Operational Matrix of Derivative
The differentiation of vector ![]() in 5 can be expressed as [15]
in 5 can be expressed as [15]
![]()
where ![]() is
is ![]() operational matrix of derivative for trigonometric scaling function. Suppose
operational matrix of derivative for trigonometric scaling function. Suppose
![]() (6)
(6)
where ![]() and
and![]() . So the matrix
. So the matrix ![]() can be respresented as a block matrix as
can be respresented as a block matrix as
![]()
where ![]() and
and ![]() are
are ![]() matrices. The entries of matrices
matrices. The entries of matrices ![]() and
and ![]() may be finding by using 3
may be finding by using 3
![]()
where ![]() is a
is a ![]() zero matrix,
zero matrix, ![]() is a
is a ![]() identity matrix. Using
identity matrix. Using ![]() we get
we get
![]() (7)
(7)
Using Equation (7) and ![]()
![]() we get
we get
![]() (8)
(8)
and
![]() (9)
(9)
for![]() .
.
4. Function Approximation
In this section, we give the concrete computational schemes for this integral Equation (2) with the Green’s function kernel. The discretization form of (2) is given in the following subsection.
By introducing a basis ![]() for the subspace
for the subspace![]() , the coefficients vector
, the coefficients vector ![]() of the discrete solution
of the discrete solution ![]() is defined by
is defined by
![]() (10)
(10)
where ![]() is
is ![]() unknown vector defined similar to (5). Using (2) we get
unknown vector defined similar to (5). Using (2) we get
![]() (11)
(11)
We tries to solve the above function by picking approximate values for![]() ,
, ![]() and
and![]() . While only defined for the interval [−1, 1], this is a universal function actually, because we can convert the limits of inte- gration for any interval
. While only defined for the interval [−1, 1], this is a universal function actually, because we can convert the limits of inte- gration for any interval ![]() to the Legendre-Gauss or
to the Legendre-Gauss or ![]() interval
interval![]() :
:
![]() (12)
(12)
The abscissas ![]() and weights
and weights ![]() to be used have been tabulated and are easily availabe; Table 1 gives the values up to six points. Also included in the table is the form of the error term
to be used have been tabulated and are easily availabe; Table 1 gives the values up to six points. Also included in the table is the form of the error term ![]() that corresponds to
that corresponds to![]() , and it can be used to determine the accuracy of the Gauss-Legendre integration formula.
, and it can be used to determine the accuracy of the Gauss-Legendre integration formula.
Applying Equation (10) in Equation (12) we have
![]() (13)
(13)
By substituting ![]() in (1), we have a linear system. Now for determining unknown coefficients
in (1), we have a linear system. Now for determining unknown coefficients ![]() and
and![]() , we choose collocation method With collocation points as
, we choose collocation method With collocation points as
![]() (14)
(14)
![]() (15)
(15)
Thus, we have system of linear equation ![]() where
where![]() ,
, ![]() ,
, ![]() is the points of Gauss-Legendre, and
is the points of Gauss-Legendre, and
![]()
![]()
Table 1. Gauss-legendre abscissas and weights.
![]()
![]()
![]()
![]()
So, the unknown function ![]() can be found. Note that we find the function by MATLAB.
can be found. Note that we find the function by MATLAB.
5. Numerical Example
To support our theoretical discussion, we applied the method presented in this paper to several examples. All the generalized Green’s function kernels in this numerical example are solved by trigonometric wavelet. Our me- thod compared with exact solution.
Example. Consider the inhomogeneous differential equation with the following coditions:
![]() (16)
(16)
The exact solution is![]() . If we solve above problem with Green’s function, we have
. If we solve above problem with Green’s function, we have![]() . The linear algebraic system is solved by the steepest
. The linear algebraic system is solved by the steepest
descent method and results are shown in Figure 1. The relative errors between ![]() and
and ![]() in absulote error are given in Table 2 and Table 3, and different Gauss-Legendre Abscissas and Weights. It is easy to see that our error results are greatly small with low computing cost.
in absulote error are given in Table 2 and Table 3, and different Gauss-Legendre Abscissas and Weights. It is easy to see that our error results are greatly small with low computing cost.
The above example states
1. Our numerical method is also efficient when the wave number J is very large, that is to say, the wave number J can hardly affect the convergence rate,
2. Our numerical method is very fast, for example, the run time is only 2.000 s as J = 8, for which the corresponding matrix ![]() is
is![]() .
.
6. Conclusion
The trigonometric scaling function is used to solve the Green’s function of an inhomogeneous differential equation. Some properties of trigonometric scaling function are presented and the operational matrices of derivative for trigonometric scaling function are utilized to reduce the solution of Green’s function to the solution of linear
![]() (a) (b)
(a) (b)
Figure 1. (a) Result for J = 1 and N = 3; (b) Result for J = 3 and N = 3.
![]()
Table 2. Error analysis and numerical results of example for J = 1 and N = 3.
![]()
Table 3. Error analysis and numerical results of example for J = 3 and N = 3.
system of equations with sparse matrix of coefficients. Applications of the wavelets allow the creation of more effective and faster algorithms than the ordinary ones. Illustrative examples are included to demonstrate the vali- dity and applicability of the technique. The main advantage of this method is its simplicity and small com- putation costs.
Acknowledgements
The authors are very grateful to both refrees for carefully reading the paper and for comments and suggestions which have improved the paper.