Modelling and Simulation of the Spread of HBV Disease with Infectious Latent

I. A. Moneim^1,2, H. A. Khalil^1,3

¹Department of Basic and Applied Science, Unaizah Community College, Qassim University, Unaizah, Saudi Arabia.
²Department of Scientific Computing, Faculty of Computers and Information, Benha University, Benha, Egypt.
³Department of Mathematics, Faculty of Science, Zagazig University, Zagazig, Egypt.

DOI: 10.4236/am.2015.65070                

Abstract

This paper studies the global behavior of the spread of HBV using a SEIR model with a constant vaccination rate. The infectivity during the incubation period is considered as a second way of transmission. The basic reproduction number R0 is derived as a function of the two contact rates β1 and β2 . There is a disease free equilibrium point (DFE) of our model. When R0 < 1, the (DFE) is asymptotically stable. On the other hand, if R0 > 1, there is a unique endemic equilibrium. We proved that the endemic equilibrium was globally asymptotically stable when R0 > 1 and that the disease persisted in the population. These results are original for our model with vaccination and two contact rates.

Keywords

HBV Modelling, Global Stability, Simulation, Two Contact Rates, Basic Reproduction Number R0

1. Introduction

Spread of the HBV is a major public health problem. About a third of the worlds population, approximately 2 billion people, get infected with hepatitis B virus in their life time. About 360 million people remain chronically infected carriers of the disease, most of whom are unaware of their HBV status [1] and about 20% - 30% of whom will eventually die from chronic sequel. The prevalence of HBV infection varies from country to country, depending upon a complex behavioral, environmental and host factors [2] . Chronic HBV can lead to hepatocellular carcinoma after 20 years among persons with chronic HBV infection; the risk for premature death from cirrhosis or hepatocellular carcinoma is 15% - 25% [3] .

Medical observations and statistics show that there are many ways for HBV transmission. Blood to blood product and shared syringes act as medical transmissions for the HBV in the developing countries. Also, HBV can transmit through the use of shared razors and brushes. Mosquitoes and bed-bugs can play as another sort of blood to blood tool to transfer the virus. It has been reported that the HBV can be transmitted among sexual partners. Finally, mothers can pass the infection to their children during pregnancy or breast feeding [4] .

It is well documented that many diseases, such as tuberculosis, HIV/AIDS and SARS, etc., have a contagious latent period; a latent individual can transmit the disease to the susceptible. This means that there are two forces of infection during both the latent and infectious periods. This fact has been noticed by some researchers [5] - [7] . HBV has a long incubation period which varies from six weeks to six months. The latent persons can pass the HBV infection during their latent period [3] . So, we add another sort of transmission of the HBV. This second way comes from the contact between the latent persons and the susceptibles.

Li and Jin [5] consider a SEI epidemic model with general contact rate that incorporates constant recruit- ment and has infectious forces in both the latent and infected periods. In their work, Lyapunov function and LaSalles invariant set theorem have been used to prove the global asymptotical stable results of the disease-free equilibrium. They studied the stability of the epidemic equilibrium by using the Poincare Bendixson property. Also, Li and Jin [6] present a SEIR model which has infectious forces in latent, infected and immune period.

Li and Fang [8] studied an age structured SEIR epidemic model with infectivity in both the latent and in- fectious periods. By using the theory and methods of Differential and Integral Equations, they obtained that the disease-free equilibrium was expression for the basic reproduction number locally and globally asymptotically stable if. In this case, the disease always dies out. When, there exists a unique endemic equili- brium which is asymptotically stable under certain conditions [8] .

2. The Model

We have considered a more complicated and realistic SEIR model with vaccination. This type of model which takes account of the infectiousness of disease in the latency state. Here we investigate the effect of the infectivity of the latent population in addition to the transmission between the susceptibles and infective populations. The model makes the following assumptions:

1) The total population size is a constant N, and the population is divided into four groups:

a) The susceptible class, S, comprising those people who are capable of catching the disease;

b) The exposed (or latent) class, , comprising those individuals who are infected but not yet infectious;

c) The infectives, 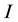, comprising those who are infected and capable of transmitting the disease;

d) The recovered class, 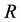, comprising those individuals who are immune.

2) The per capita birth rate is a constant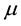. As births balance deaths we must have that the per capita death rate is also.

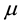3) The population is uniform and mixes homogeneously.

4) The infection rates and are defined as the total rates at which potentially infectious contacts occur between two individuals (in other words contacts which will result in the transmission of infection if one of the individuals is susceptible and the other is infectious for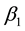) and latent for.

5) The exposed individuals move from the latent class to the infective class at a constant rate 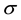and so the average latent period, conditional on survival to the end of it, is.

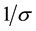6) The infectives move from the infective class to the recovered class at a constant rate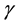, where is the average infectious period, conditional on survival to the end of it.

The SEIR model for the spread of infectious diseases can be written as a set of four coupled non-linear ordinary differential equations as follows:

(1)

, (2)

, (3)

and (4)

with.

The basic reproduction number is defined as the average value of the expected number of secondary cases produced by a single newly infected person entering the population at the disease free state. In this model the average value of the expected number of secondary cases produced by a single infected person is

(5)

It has been shown that with constant transmission rates and our model has one and only one disease free equilibrium (DFE) and another endemic equilibrium state of our SEIR model. In this paper, simulation results have been conducted for parameter values which insure that if the vaccination parameter is not large enough, to force the basic reproductive number to be less than one in value, the disease remains endemic in the population. In the other hand simulations of our model are conducted to show up the effect of introducing the disease transmission between latent and susceptible populations.

3. Equilibrium Points

The system (1)-(4) has two equilibria points the first one is the disease free equilibrium (DFE) point:

where, and. The other one is the endemic equilibrium point which is represented by

where, , and.

Here, it straightforward to show that, exists if and only if.

4. Stability of the Disease Equilibrium Point (DFE)

This section studies the stability of the disease free equilibrium (DFE) point. In this case, there is no disease in the population as. The Jacobian matrix of the system (1)-(4) at the point, (DFE) is given by

(6)

Theorem 1 The disease free equilibrium point, is locally asymptotically stable for the system (1)-(4) if, and unstable when.

Proof

From the characteristic equation of the matrix (6) we have two negative eigenvalues, both of them equals to. The rest of the characteristic equation is given by,

From Equation (5), if, then. So, we found that all the eigenvalues of the matrix (6) have negative real parts. Therefore, using the Routh-Hurwitz conditions for the stability of linear differential Equ- ations [9] , the disease free equilibrium point is locally asymptotically stable if. If this implies that. Thus the characteristic equation of the matrix (6) must have a positive eigenvalue. Therefore, the disease free equilibrium point, is unstable for the system (1)-(4). This completes the proof of Theorem (1).

5. Global Stability of the Endemic Equilibrium Point

This section concerned with global stability of the endemic equilibrium point. The necessary and sufficient con- dition to the existence of the endemic point, is that. Similar technique to the proof to Theorem 1 in Korobeinikov and Wake [10] is been used in this section.

We start off by calculating the parameter values of the model at the equilibrium. From Equation (1) at the equilibrium, we have that, therefore

. (7)

Similarly, from Equation (2), we get,

. (8)

finally, from Equation (3), we can deduce that,

(9)

Substituting in (1), (2) and (3), we find that,

(10)

(11)

and (12)

Let, , and. Then substituting these values in Equations (10)-(12) we find that,

(13)

(14)

and (15)

Theorem 2 If, then the endemic equilibrium point, is globally asymptotically stable for the system (1)-(4).

Proof

Define a positive definite function such that, where

, and. Now we prove that, is nonpositive definite function. Differentiat-

ing and substituting by the values of, and we have,

(16)

(17)

(18)

. (19)

therefore,

(20)

. (21)

Rearranging Equation (21) we deduce that,

. (22)

As the arithmetic mean is greater than or equal to the geometric mean we find that, iff

and all of and e are nonnegative. Equation (7) ensures that,. Moreover iff

and which can be represented by the following set,

. (23)

The equilibrium point is the only invariant set of the system (1)-(4) which contained entirely in the set. Hence by Liapunov’s direct methods is globally asymptotically stable if for the system (1)-(4). This completes the proof of Theorem (2).

6. Simulation Results

In this section we study numerically the behaviour of the system. The system of linear ordinary differential Equations (1)-(4) is been solved numerically by using the software package XPPAUTO and using the following parameter set from the literature, [4] [11] - [13] . Also we simulate our system for two different states one if and the other one when we found that, disease has a thre- shold level for the reproductive number to be under one in value which the disease to die out. If the vaccination value is not sufficient then stays above one in value and the disease becomes endemic.

The first result of our simulations confirms that the disease free equilibrium is globally asymptotically stable when. On the other hand if there is a stable endemic solution. Here we present a sample of the results obtained in these simulations. We give a sample of the effect of considering the transition rate between latent and susceptibles. Also we give a bifurcation diagram of the infected population against the vaccination rate. Figure 1(a) shows that when the values of the infected population tends to its disease free equilibrium values. Figure 1(b) shows that when the vaccination fails to force the basic reproduction number to be less than one in value the disease fires up and approaches an endemic level. This result is obtained for the case that the vaccination rate.

Figure 2 studies numerically the behaviour of the system in response to changes in p, the vaccination rate. We use the basic idea that, sectioning the endemic stable equilibrium solutions by looking at Poincaré sections and plotting the sections of the endemic equilibrium solutions against the vaccination value p to obtain the number

Figure 1. The number of infected population against time corresponding to parameter values of HBV (a) when the vaccination rate (p = 0.96) which is large enough so that, R₀ < 1 and (b) when the vaccination rate, p = 0.5, is not sufficient enough to keep R₀ < 1.

of points in each section [14] . These points represent the period of the stable long term periodic solution of our model. We have taken the simulation parameters for all of the bifurcation diagrams presented here as stated above and the total population size N was 1,000,000.

Figure 2 represents the bifurcation diagram for HBV with two transmission rates for the infected and the susceptibles. This figure shows that at small values of vaccination parameter the disease has a periodic solution of period one year. Increasing the value of produces a two year periodic further increases generate a series of period doubling solutions until the behaviour of the system appears to become aperiodic and possibly chaotic. However, increasing the vaccination rate more forces the infected number to drop down until approaching zero at.

Figure 2 represents the number of infected population against time corresponding to parameter values of HBV when. The black line plots the infected against time when, the latent are infectious. In this case, there is another contact rate between susceptibles and latent. The black line shows that, there is an endemic solution which is going up rapidly. This solution has some peaks which look to be periodic of long period. The

Figure 2. The bifurcation diagrams of HBV parameter values of the number of infected against vaccination parameter p.

red line plots the infected against time when infectivity of the latent is ignored. The red line in Figure 2 shows that there are some peaks which have larger tops than the black one but, the line has small values all over the whole diagram. The green line represents the case that, there is a total isolation of the infected persons. The green line shows the smallest peaks in the diagram. These peaks decay smoothly to be almost steady state.

7. Summary and Discussion

This paper investigates the effect of using another way of producing new cases. This way is the fact that latent persons can pass the disease into susceptibles [3] . Also, vaccination of all newborns, at a constant rate, has been considered. It is documented that vaccination strategies are applied worldwide to vaccinate children in the early ages. For example, in China an effective vaccination program has been established for newborn babies since the 1990s, which has reduced chronic HBV infection in children. Unfortunately, the incidence of hepatitis B is still increasing [13] . This means that the vaccinated proportion is large enough to force the reproduction number to be less than one in value. Therefore, to control HBV infection vaccination, strategies need a treatment scheme as another leg to have a better control strategy for the disease [15] .

The first result of this paper comes from the stability analysis of the DFE of our model. We find that the DFE is locally asymptotically stable when, the basic reproduction number, is less than one. If exceeds one, then the DFE point is unstable. When, there exists another equilibrium point which is the endemic point. We deduced that if, then is globally asymptotically stable for the system (1)-(4). We used Liapunov’s direct methods to prove this result.

Simulation results of our model have been conducted for HBV parameter set using different vaccination parameter values. From these results, we find that there is a critical ratio approximately, from which all the newborns must be vaccinated. This value is the sufficient condition to reduce susceptible number to be less than a critical value S_C. This forces the basic reproduction number to be less than one in value and the disease dies out. The threshold value can be driven as follows. From Equation (5), we have that

. Therefore, to keep, we must keep the susceptibles below the certain threshold

value which is given by

(24)

Figure 3. The number of infected population against time corresponding to parameter values of HBV when the vaccination rate is not sufficient enough to keep R₀ < 1, the black, red and green lines corresponding to (β₁ = β₂ = 0.000025), (β₁ = 0.000025, β₂ = 0) and (β₁ = 0, β₂ = 0.000025) respectively.

If this condition fails, the susceptibles will be large enough to make the disease firs up and become endemic in the population. In this case, we got some high peaks as shown in Figure 3. It is important to note that Figure 3 indicates that the black line which includes the infectivity of the latent is going up continuously and has a sustainable long term period solution.

The bifurcation diagram Figure 2 indicates that the vaccination parameter p can play as a key value of our model. This figure also shows that there are many endemic periodic solutions of our model. These solutions vary from biennial to large period or chaotic solutions. It is obvious to conclude that bifurcation diagram Figure 2 gives a wide range of information about the dynamics of the HBV disease and indicates how the values of the vaccination rate affect the behaviour of the disease dynamics.

Finally, vaccinating all newborns by a rate greater than 96% is not reachable in practice. Therefore, from our results, it is important to declare that treatments or additional vaccination strategies are needed to control the spread of HBV in population. Controlling the disease means that reducing the susceptibles by vaccination or reducing latent and infected by treatments scheme.

Acknowledgements

This research is funded by the deanship of scientific research, Qassim University, KSA.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Abdulrahman, S., Akinwande, N.I., Awojoyogbe, O.B. and Abubakar, U.Y. (2013) Sensitivity Analysis of the Parameters of a Mathematical Model of Hepatitis B Virus Transmission. Universal Journal of Applied Mathematics, 1, 230-241.
[2]	Saher, F., Rahman, K., Quresh, J.A., Irshad, M. and Iqbal, H.M. (2012) Investigation of an Inflammatory Viral Disease HBV in Cardiac Patients through Polymerase Chain Reaction. Advances in Bioscience and Biotechnology, 3, 417-422. http://dx.doi.org/10.4236/abb.2012.324059
[3]	Centers for Disease Control and Prevention (2012) http://www.cdc.gov/hepatitis/HBV
[4]	Moneim, I.A., Al-Ahmed, M. and Mosa, G.A. (2009) Stochastic and Monte Carlo Simulation for the Spread of the Hepatitis B. Australian Journal of Basic and Applied Sciences, 3, 1607-1615.
[5]	Li, G. and Jin, Z. (2005) Global Stability of an SEI Epidemic Model with General Contact Rate. Chaos, Solitons and Fractals, 23, 997-1004.
[6]	Li, G. and Jin, Z. (2005) Global Stability of a SEIR Epidemic Model with Infectious Force in Latent, Infected and Immune Period. Chaos, Solitons and Fractals, 25, 1177-1184. http://dx.doi.org/10.1016/j.chaos.2004.11.062
[7]	Li, G., Wang, W. and Jin, Z. (2006) Global Stability of an SEIR Epidemic Model with Contact Immigration. Chaos, Solitons and Fractals, 30, 1012-1019. http://dx.doi.org/10.1016/j.chaos.2005.09.024
[8]	Li, X. and Fang, B. (2009) Stability of an Age-Structured SEIR Epidemic Model with Infectivity in Latent Period. Applications and Applied Mathematics: An International Journal (AAM), 4, 218-236.
[9]	Kapur, J.N. (1990) Mathematical Models in Biology and Medicine. Affiliated East-West Press, New Delhi.
[10]	Korobeinikov, A. and Wake, G.C. (2002) Lyapunov Functions and Global Stability for SIR, SIRS, and SIS Epidemiological Models. Applied Mathematics Letters, 15, 955-960. http://dx.doi.org/10.1016/S0893-9659(02)00069-1
[11]	Zhuo, X. (2011) Global Analysis o f a General HBV Infection Model. IEEE International Conference on Systems Biology (ISB), Zhuhai, 2-4 September 2011, 978-1-4577-1666-9/11.
[12]	Wiah, E.N., Dontwi, I.K. and Adetunde, I.A. (2011) Using Mathematical Model to Depict the Immune Response to Hepatitis B Virus Infection. Journal of Mathematics Research, 3, 157-116. http://dx.doi.org/10.5539/jmr.v3n2p157
[13]	Zou, L., Zhang, W. and Ruan, S. (2010) Modeling the Transmission Dynamics and Control of Hepatitis B Virus in China. Journal of Theoretical Biology, 262, 330-338. http://dx.doi.org/10.1016/j.jtbi.2009.09.035
[14]	Greenhalgh, D. and Moneim, I.A. (2003) SIRS Epidemic Model and Simulations Using Different Types of Seasonal Contact Rate. Systems Analysis Modelling Simulation, 43, 573-600. http://dx.doi.org/10.1080/023929021000008813
[15]	Kimbir, A.R., Aboiyar, T., Abu, O. and Onah, E.S. (2014) Simulation of A Mathematical Model of Hepatitis B Virus Transmission Dynamics in the Presence of Vaccination and Treatment. Mathematical Theory and Modeling, 4, 44-59.