On Eigenvalues and Boundary Curvature of the Numerical Rang of Composition Operators on Hardy Space ()
1. Introduction
For a bounded linear operator A on a Hilbert space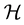 , the numerical range
, the numerical range 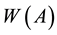 is the image of the unit sphere of
is the image of the unit sphere of 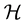 under the quadratic form
under the quadratic form 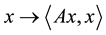 associated with the operator. More precisely,
associated with the operator. More precisely,
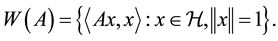
Thus the numerical range of an operator, like the spectrum, is a subset of the complex plane whose geometrical properties should say something about the operator.
One of the most fundamental properties of the numerical range is its convexity, stated by the famous Toeplitz-Hausdorff Theorem. Other important property of 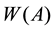 is that its closure contains the spectrum of the operator,
is that its closure contains the spectrum of the operator, 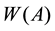 is a connected set with a piecewise analytic boundary
is a connected set with a piecewise analytic boundary ![]() [1] .
[1] .
Hence, for all but finitely many points![]() , the radius of curvature
, the radius of curvature ![]() of
of ![]() at p is well defined. By convention,
at p is well defined. By convention, ![]() if p is a corner point of
if p is a corner point of![]() , and
, and ![]() if p lies inside a flat portion of
if p lies inside a flat portion of![]() .
.
Let ![]() denote the distance from p to
denote the distance from p to![]() , we define
, we define ![]() the smallest constant such that
the smallest constant such that
![]() (1)
(1)
for all ![]() with finite non-zero curvature.
with finite non-zero curvature.
By Donoghue’s theorem ![]() whenever
whenever![]() . Therefore,
. Therefore, ![]() for all convexoid element A. Recall that convexoid element is an element such that its numerical range coincides with the convex hull of its spectrum. For non-convexoid A,
for all convexoid element A. Recall that convexoid element is an element such that its numerical range coincides with the convex hull of its spectrum. For non-convexoid A,
![]() (2)
(2)
where the supremum in the right-hand side is taken along all points ![]() with finite non-zero curvature.
with finite non-zero curvature.
The computation of ![]() for arbitrary
for arbitrary ![]() matrix A is an interesting open problem. For
matrix A is an interesting open problem. For![]() , we do not have an exact value of
, we do not have an exact value of![]() . The question whether there exists a universal constant
. The question whether there exists a universal constant![]() , posed by Mathias [2] . Caston, et al. [3] prove the following inequalities:
, posed by Mathias [2] . Caston, et al. [3] prove the following inequalities:
![]() (3)
(3)
Mirman a sequence of ![]() Toeplitz nilpotent matrices
Toeplitz nilpotent matrices ![]() with
with ![]() algrowing asymptotically as
algrowing asymptotically as ![]() is also found [3] . Hence, the answer to Mathias question is negative. However, the lower bound in (3) is still of some interest, at least for small values of n. The question of the exact rate of growth of
is also found [3] . Hence, the answer to Mathias question is negative. However, the lower bound in (3) is still of some interest, at least for small values of n. The question of the exact rate of growth of ![]() (it is
(it is![]() , or n, or something in between) remains open.
, or n, or something in between) remains open.
2. Composition Operator on Hardy Space
Let ![]() denote the open unit disc in the complex plane, and the Hardy space H2 the functions
denote the open unit disc in the complex plane, and the Hardy space H2 the functions ![]()
holomorphic in ![]() such that
such that![]() , with
, with ![]() denoting the n-th Taylor coefficient of f. The
denoting the n-th Taylor coefficient of f. The
inner product inducing the norm of ![]() is given by
is given by![]() . The inner product of two functions f and g in
. The inner product of two functions f and g in ![]() may also be computed by integration:
may also be computed by integration:
![]()
where ![]() is positively oriented and f and g are defined a.e. on
is positively oriented and f and g are defined a.e. on ![]() via radial limits.
via radial limits.
For each holomorphic self map ![]() of
of ![]() induces on
induces on ![]() a composition operator
a composition operator ![]() defined by the equation
defined by the equation![]() . A consequence of a famous theorem of J. E. Littlewood [4] asserts that
. A consequence of a famous theorem of J. E. Littlewood [4] asserts that ![]() is a bounded operator. (see also [5] [6] ).
is a bounded operator. (see also [5] [6] ).
In fact (see [6] )
![]()
In the case![]() , Joel H. Shapiro has been shown that the second inequality changes to equality if and only if
, Joel H. Shapiro has been shown that the second inequality changes to equality if and only if ![]() is an inner function.
is an inner function.
A conformal automorphism is a univalent holomorphic mapping of ![]() onto itself. Each such map is linear fractional, and can be represented as a product
onto itself. Each such map is linear fractional, and can be represented as a product![]() , where
, where
![]()
for some fixed ![]() and
and ![]() (See [7] ).
(See [7] ).
The map ![]() interchanges the point p and the origin and it is a self-inverse automorphism of
interchanges the point p and the origin and it is a self-inverse automorphism of![]() .
.
Each conformal automorphism is a bijection map from the sphere ![]() to itself with two fixed points (counting multiplicity). An automorphism is called:
to itself with two fixed points (counting multiplicity). An automorphism is called:
elliptic if it has one fixed point in the disc and one outside the closed disc;
hyperbolic if it has two distinct fixed point on the boundary![]() , and
, and
parabolic if there is one fixed point of multiplicity 2 on the boundary![]() .
.
For![]() , an r-dilation is a map of the form
, an r-dilation is a map of the form![]() . We call r the dilation parameter of
. We call r the dilation parameter of ![]() and in the case that
and in the case that![]() ,
, ![]() is called positive dilation. A conformal r-dilation is a map that is conformally conjugate to an
is called positive dilation. A conformal r-dilation is a map that is conformally conjugate to an ![]() -dilation, i.e., a map
-dilation, i.e., a map![]() , where
, where ![]() and
and ![]() is a conformal automorphism of
is a conformal automorphism of![]() .
.
For![]() , an w-rotation is a map of the form
, an w-rotation is a map of the form![]() . We call w the rotation parameter of
. We call w the rotation parameter of![]() . A straightforward calculation shows that every elliptic automorphism
. A straightforward calculation shows that every elliptic automorphism ![]() of
of ![]() must have the form
must have the form
![]()
for some ![]() and some
and some![]() .
.
3. Main Results
In [8] , the shapes of the numerical range for composition operators induced on ![]() by some conformal automorphisms of the unit disc specially parabolic and hyperbolic are investigated.
by some conformal automorphisms of the unit disc specially parabolic and hyperbolic are investigated.
In [9] , V. Matache determined the shapes ![]() in the case when the symbol of the composition operator the inducing functions are monomials or inner functions fixing 0. The numerical ranges of some compact composition operators are also presented.
in the case when the symbol of the composition operator the inducing functions are monomials or inner functions fixing 0. The numerical ranges of some compact composition operators are also presented.
Also, in [10] the spectrum of composition operators are investigated.
This facts will help in discussing and proving many of the results below.
Remark 3.1 If![]() ,
, ![]() , then
, then ![]() and
and ![]() is a closed ellipticall disc whose boun-
is a closed ellipticall disc whose boun-
dary is the ellipse of foci 0 and 1, having major/minor axis of length ![]() and
and![]() . There- fore
. There- fore![]() .
.
Remark 3.2 If![]() ,
, ![]() , then
, then ![]() the closure of
the closure of![]() . If w is the n-th root
. If w is the n-th root
of unity then ![]() is the convex hull of all the n-th roots of unity and so
is the convex hull of all the n-th roots of unity and so![]() . If w is not a root of
. If w is not a root of
unity the ![]() is the union of
is the union of ![]() and the set
and the set![]() . In this case also
. In this case also![]() .
.
Remark 3.3 If ![]() is hyperbolic with fixed point a,
is hyperbolic with fixed point a, ![]() , then
, then
![]()
and ![]() is a disc center at the origin. Therefore
is a disc center at the origin. Therefore ![]() where
where ![]() is the numerical radius of
is the numerical radius of![]() .
.
Remark 3.4 If ![]() is parabolic, then
is parabolic, then ![]() and
and ![]() is a disc center at the origin. Therefore
is a disc center at the origin. Therefore
![]() .
.
Remark 3.5 If ![]() is elliptic with rotation parameter w, and w is not a root of unity, then
is elliptic with rotation parameter w, and w is not a root of unity, then ![]() and
and
![]() is a disc center at the origin. Therefore
is a disc center at the origin. Therefore![]() .
.
Therefore we have the following table for![]() .
.
Completing the Table
An elliptic automorphism ![]() of
of ![]() that does not fix the origin must have the form
that does not fix the origin must have the form![]() , where
, where
![]()
for some fixed ![]() and
and ![]() If we wish to show this dependence of
If we wish to show this dependence of ![]() on p and w, we will denote the elliptic automorphism
on p and w, we will denote the elliptic automorphism ![]() by
by![]() .
.
If ![]() is periodic then, surprisingly, the situation seems even murkier: For period 2 has been shown the closure of
is periodic then, surprisingly, the situation seems even murkier: For period 2 has been shown the closure of ![]() is an elliptical disc with foci at
is an elliptical disc with foci at ![]() (Corollary 4.4. of [8] ). It is easy to see that
(Corollary 4.4. of [8] ). It is easy to see that ![]() is open, also in [11] , the author completely determined
is open, also in [11] , the author completely determined ![]() for period 2.
for period 2.
Theorem 3.6 If ![]() is an elliptic automorphism with order 2 and P it’s only fixed point in open unit disc, then there is
is an elliptic automorphism with order 2 and P it’s only fixed point in open unit disc, then there is ![]() such that
such that
![]()
Proof. Let the operator A be self-inverse, i.e., ![]() but
but![]() , so
, so ![]() is an ellipse with foci at ±1 [12] . If
is an ellipse with foci at ±1 [12] . If ![]() with
with![]() . Then
. Then
![]()
If ![]() is an elliptic automorphism with order 2 and p it’s only fixed point in open unit disc, then
is an elliptic automorphism with order 2 and p it’s only fixed point in open unit disc, then ![]()
where![]() . Since
. Since ![]() is a nontrivial self-inverse operator on Hardy space
is a nontrivial self-inverse operator on Hardy space ![]() and
and ![]() is an inner
is an inner
function, then
![]()
and so there is ![]() such that:
such that:
![]()
But for period ![]() then all we can say is that the numerical range of
then all we can say is that the numerical range of ![]() has k-fold symmetry and we strongly suspect that in this case the closure is not a disc. Because the numerical range in this case is an open problem, so the completing of
has k-fold symmetry and we strongly suspect that in this case the closure is not a disc. Because the numerical range in this case is an open problem, so the completing of ![]() is also open problem.
is also open problem.
Acknowledgements
I thank the editor and the referee for their comments. Also, when the author is the responsible of establishing Center for Higher Education in Eghlid he is trying to write this paper, so I appreciate that center because of supporting me in conducting research.