Critical Theory of Two-Dimensional Mott Transition: Integrability and Hilbert Space Mapping ()
1. Introduction
The physical properties of strongly correlated electron systems are difficult to predict or even to describe, mainly because of the lack of suitable reliable tools to study them. Among these systems, the Mott Insulators (i.e., electronic systems which undergo a metal-insulator transition driven by correlations) have a prominent place. Most of the studies of the Mott transition are based on the microscopic dynamics of the electron system. The models are defined by an electron Hamiltonian that is then solved either by some approximation or by numerical methods. Both methods have their limitations, which have been discussed, e.g., in [1] . As of today, there are two basic tools to study the Mott transition that complement themselves. One is the Dynamical Mean Field Theory (DMFT) method, valid in the limit of infinite space dimensions [2] . The other tool is the use of integrability properties such as the Bethe Ansatz or bosonization techniques in some specific models, mostly in one spatial dimension. Different, non-perturbative approaches to models that display some form of Mott transition are therefore desirable. One such approach is that of the EFTs [3] , which has been shown to be a powerful tool for dealing with strongly correlated systems (in particle, condensed matter physics and statistical mechanics, among other areas of knowledge). The EFT in condensed matter physics has its roots in Landau’s ideas of effective degrees of freedom and their characterization throughout symmetry. It has been further developed after the introduction of the Renormalization Group ideas following Wilson’s approach. The main idea is to first identify the characteristic effective degrees of freedom of a given system at a given energy scale (usually arising from the phenomenology), identifying their symmetries and then writing down the most general Hamiltonian (or Lagrangian) compatible with those symmetries.
For the case of the Mott transition, we have applied the EFT method to a fermion model on the lattice with density-density coupling in a previous paper [4] . In that article, we have provided an extension of the method of integrability to a (2 + 1)-dimensional spinless fermion model with nearest neighbors Coulomb interactions, having written down an Effective Field Theory (EFT) to further study the properties of the model at the Mott transition critical point. The goal of the present article is to reformulate this approach in a different, perhaps more straightforward fashion which could be useful for future developments and generalizations, and to shown that the EFT previously obtained is actually the corresponding (equivalent) field theory at the level of the Hilbert space at the critical point. Moreover, under this approach, we will show that, the Mott transition is characterized as a change in the ground state.
2. Fermionic Model and Its Integrability
We start by considering the following Hamiltonian model:
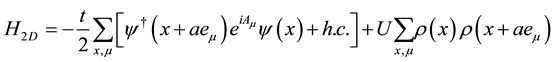 (1)
(1)
where 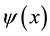 is the fermion field, x labels the lattice sites and
is the fermion field, x labels the lattice sites and 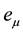 are the unit lattice vectors pointing to the nearest neighbors of a given site, a is the lattice spacing, t is the hopping parameter,
are the unit lattice vectors pointing to the nearest neighbors of a given site, a is the lattice spacing, t is the hopping parameter, 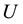 is the (constant) Coulomb potential,
is the (constant) Coulomb potential, 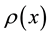 is the charge density (normal-ordered with respect to the half-filling ground state),
is the charge density (normal-ordered with respect to the half-filling ground state), 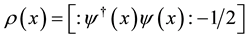 and
and 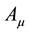 is an Abelian statistical gauge field defined on the links of the lattice.
is an Abelian statistical gauge field defined on the links of the lattice.
This model can be mapped into the two-dimensional anisotropic Heisenberg (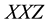 spin) model by means of a two-dimensional Jordan-Wigner transformation [5] :
spin) model by means of a two-dimensional Jordan-Wigner transformation [5] :
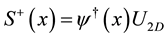 (2)
(2)
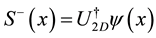 (3)
(3)
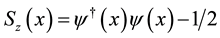 (4)
(4)
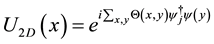 (5)
(5)
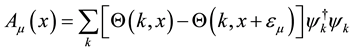 (6)
(6)
where 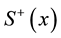 and
and 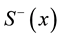 are the rising and lowering spin operators for spin one-half particles, and
are the rising and lowering spin operators for spin one-half particles, and 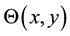 is the lattice angle between two points in a two-dimensional square lattice.
is the lattice angle between two points in a two-dimensional square lattice.
The partition function of the two-dimensional Heisenberg model, in the Hamiltonian framework, can be written as:
![]() (7)
(7)
where ![]() is the Quantum (Hilbert) space,
is the Quantum (Hilbert) space, ![]() is the row-space,
is the row-space, ![]() is the column-space, and
is the column-space, and ![]() is the layer-to-layer transfer matrix given by:
is the layer-to-layer transfer matrix given by:
![]() (8)
(8)
![]() (9)
(9)
where![]() . The integrability of the model requires the commutativity of the layer-to-layer transfer matrices, which is guaranteed by the existence of solutions of the Zamolodchikov Tetrahedron equation (ZTE) ([6] )
. The integrability of the model requires the commutativity of the layer-to-layer transfer matrices, which is guaranteed by the existence of solutions of the Zamolodchikov Tetrahedron equation (ZTE) ([6] )
![]() (10)
(10)
where, we have made some abuse of notation since now ![]() could be the quantum-Hilbert space or the row/ column sates.
could be the quantum-Hilbert space or the row/ column sates.
As it is known, the ![]() -matrix provides an intertwining for the layer-to-layer transfer matrix (or, equivalently, for the
-matrix provides an intertwining for the layer-to-layer transfer matrix (or, equivalently, for the ![]() operators), i.e., it satisfies:
operators), i.e., it satisfies:
![]() (11)
(11)
where the ![]() operators act on the tensor product vector space
operators act on the tensor product vector space![]() . (Here the Latin index a, b, c stands for classical spin-1/2 representation spaces and numeric index stands for the quantum Hilbert spaces) The existence of solutions of the ZTE follows from the solutions of the Quantum Korepanov Equation (QKE) [7]
. (Here the Latin index a, b, c stands for classical spin-1/2 representation spaces and numeric index stands for the quantum Hilbert spaces) The existence of solutions of the ZTE follows from the solutions of the Quantum Korepanov Equation (QKE) [7]
![]() (12)
(12)
which codifies the zero-curvature condition of a “quantum scattering problem”. Here ![]()
![]() represent a algebra of observables and
represent a algebra of observables and ![]() acts on the direct sum of vector spaces
acts on the direct sum of vector spaces![]() . In an outstanding series of articles, Sergeev et al. [8] [9] have shown that (under minimal conditions) the only solution of the QKE for “vertex type problems” (i.e., when the lattice problem is formulated in terms of vertex potentials) is given by:
. In an outstanding series of articles, Sergeev et al. [8] [9] have shown that (under minimal conditions) the only solution of the QKE for “vertex type problems” (i.e., when the lattice problem is formulated in terms of vertex potentials) is given by:
![]()
where ![]() means that the operators in the Korepanov matrix carry representations of the
means that the operators in the Korepanov matrix carry representations of the ![]() -oscillator algebra, i.e. they satisfy:
-oscillator algebra, i.e. they satisfy:
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
where q is the deformation parameter. The corresponding L operators are:
![]() (17)
(17)
where we have used ![]() and have introduced the afinization parameters
and have introduced the afinization parameters![]() . Is straightforward to show that the products of two L operators of the q-oscillator model give rise to an L operator of the Heisenberg
. Is straightforward to show that the products of two L operators of the q-oscillator model give rise to an L operator of the Heisenberg ![]() model (for details see [4] [10] ). Therefore, for a square lattice with an even number of sites (on the rows and on the columns) the partition function of the
model (for details see [4] [10] ). Therefore, for a square lattice with an even number of sites (on the rows and on the columns) the partition function of the ![]() model can be written as:
model can be written as:
![]() (18)
(18)
This means that the original model is mapped onto the q-oscillator model. It then becomes possible to study the states of the lattice fermion model (1) by analyzing the representations of the q-oscillator algebra.
For ![]() the q-oscillator algebra has Fock space representations defined by:
the q-oscillator algebra has Fock space representations defined by:
![]() (19)
(19)
![]()
![]() (20)
(20)
for ![]() and
and![]() , respectively. Furthermore, the states of the system are:
, respectively. Furthermore, the states of the system are:
![]() (21)
(21)
To achieve a deeper understanding of the solution that we have just discussed, we may use a crucial property of the ZTE. Namely, the ZTE can be projected (or reduced) onto the Yang-Baxter equation after tracing out over one (temporal or spatial) direction. Tracing out over the y-column we obtain a one-dimensional Heisenberg ![]() chain, which is known to belong to the universality class of the Luttinger liquids, impliying that the degrees of freedom of this chain are charge density waves. This observation fits within the picture of the solution as a “quantum fluctuation”. Moreover, since the ZTE can be projected on any row or column, the consistency of the theory demands that the solution must be a two-dimensional charge fluctuation on the lattice. Hence, the q parameter becomes a two-dimensional analog of the Luttinger parameter.
chain, which is known to belong to the universality class of the Luttinger liquids, impliying that the degrees of freedom of this chain are charge density waves. This observation fits within the picture of the solution as a “quantum fluctuation”. Moreover, since the ZTE can be projected on any row or column, the consistency of the theory demands that the solution must be a two-dimensional charge fluctuation on the lattice. Hence, the q parameter becomes a two-dimensional analog of the Luttinger parameter.
In order to identify the critical point with the values of the parameters in the fermion model (1) let us remind that the reduced one-dimensional model (which has a long history) have been solved in [7] , and it is known to undergo a metal-insulator (Mott transition), and a charge density wave ordering (CDW) with a breakdown of the parity symmetry above the Mott gap. This Mott transition appears when![]() , i.e., when the dimensionless parameter
, i.e., when the dimensionless parameter![]() .
.
We will now study the representations of the q-Oscillattor algebra at the Mott transition point![]() . When the deformation parameter satisties
. When the deformation parameter satisties![]() , the algebra reduces to a two independent Weyl algebras:
, the algebra reduces to a two independent Weyl algebras:
![]() (22)
(22)
which have cyclic representations for![]() ,
, ![]() given by:
given by:
![]() . (23)
. (23)
Now we claim that the “corresponding” field theory at the level of the Hilbert space is a Double-Lattice-Chern Simons theory with abelian gauge group. To show this, first we shall impose periodic boundary conditions in the original fermion model, and compactify the manifold onto a torus such that the original square lattice matches with the lattice made by the homology cycles of this torus, and consider the Abelian C-S action [11]
![]() (24)
(24)
this a topological gauge field theory with natural observables provided by Wilson Loops:
![]() . (25)
. (25)
In holomorphic coordinates, the gauge field may be decomposed as:
![]() , (26)
, (26)
where ![]() is the modular parameter of the torus, and
is the modular parameter of the torus, and![]() ,
, ![]() is a basis of holomorphic 1-forms on the torus,
is a basis of holomorphic 1-forms on the torus, ![]() is a complex parametric function. The wave functional may be written as:
is a complex parametric function. The wave functional may be written as:
![]() . (27)
. (27)
The local Gauge transformations on the CS theory are defined by:![]() . However, on the torus the gauge theory may also have global gauge transformations associated with the windings (of the Wilson loops) over the non-contractible loops around the torus. Let us denote by
. However, on the torus the gauge theory may also have global gauge transformations associated with the windings (of the Wilson loops) over the non-contractible loops around the torus. Let us denote by ![]() the gauge transformations with n and m integer winding numbers around the (orthogonal) homology cycles. These global gauge transformations have anomalous commutations relations that can be avoided by requiring the condition: (for details see [12] ):
the gauge transformations with n and m integer winding numbers around the (orthogonal) homology cycles. These global gauge transformations have anomalous commutations relations that can be avoided by requiring the condition: (for details see [12] ):
![]() (28)
(28)
where ![]()
![]() are parameters that belong to the interval
are parameters that belong to the interval![]() . These conditions are solved by the Jacobi Theta functions with solutions labeled by an integer
. These conditions are solved by the Jacobi Theta functions with solutions labeled by an integer![]() . The large Gauge transformations still act as symmetries of the Chern-Simons theory and a basis of such Gauge transformations may be written in terms of the Wilson loops as:
. The large Gauge transformations still act as symmetries of the Chern-Simons theory and a basis of such Gauge transformations may be written in terms of the Wilson loops as:
![]() , (29)
, (29)
which satisfy a Weyl-algebra:
![]() (30)
(30)
On the basis
![]() (31)
(31)
the operators (29) act as:
![]() (32)
(32)
![]() (33)
(33)
where![]() .
.
Then, taken ![]() (i.e., using bosonic boundary condition for the CS-field) and identifying
(i.e., using bosonic boundary condition for the CS-field) and identifying ![]() and
and ![]() we see that the states of the q-oscillator (and therefore the sates of the Fermion model) at
we see that the states of the q-oscillator (and therefore the sates of the Fermion model) at ![]() correspond to the states of the CS Theory (27) in the basis (31). The coupling constant of the CS theory may now be inferred in two different ways: Firstly, we note that at the Mott transition:
correspond to the states of the CS Theory (27) in the basis (31). The coupling constant of the CS theory may now be inferred in two different ways: Firstly, we note that at the Mott transition:
![]() . (34)
. (34)
Secondly, we note that the projection property of the ZTE implies that each row (or column) is a ![]() spin chain (whose critical properties are described by a Weiss-Zumino-Witten model with coupling constant
spin chain (whose critical properties are described by a Weiss-Zumino-Witten model with coupling constant![]() ), which is known to match the coupling constant of the corresponding
), which is known to match the coupling constant of the corresponding ![]() CS theory
CS theory![]() . For further details, please see our analysis in [13] ).
. For further details, please see our analysis in [13] ).
Taking into account that the degrees of freedom of the Fermion Model (1) must be restricted to a square lattice, using the fact that the q-oscillator algebra splits into two Weyl algebras and using the parity of the original model, we deduce that the corresponding (equivalent) Field Theory at the Mott critical point of the fermion model (1) is a Double Lattice Chern-Simons theory:
![]() , (35)
, (35)
with coupling constant![]() , where
, where ![]() and
and ![]() are two Abelian gauge fields of opposite chiriality (left and
are two Abelian gauge fields of opposite chiriality (left and
right), and where![]() ,
, ![]() ,
, ![]() , (where
, (where ![]() is
is
the lattice-parameter) [14] . This theory has quantum group symmetry ![]() with deforma-
with deforma-
tion parameter ![]() [12] [15] .
[12] [15] .
3. Conclusion
In this article, we have reconsidered the integrability of the two-dimensional density-density coupled fermion moldel (1), which follows from the solution of the Zamolodchikov’s Tetrahedron equation associated with the ![]() -oscillator algebra, firstly found in ([9] ). Using the representation theory of this algebra, we have constructed a explicit mapping between the states of the original fermion model at the Mott critical point
-oscillator algebra, firstly found in ([9] ). Using the representation theory of this algebra, we have constructed a explicit mapping between the states of the original fermion model at the Mott critical point ![]() and the states of the lattice Double Chern Simons theory at coupling constant
and the states of the lattice Double Chern Simons theory at coupling constant![]() . That is, we have provided an explicit link between the Hilbert spaces of a microscopic theory with those of its long distance EFT, something that can not be expected in general systems, although some researchers in the condensed matter community frequently ask for. The changes in the representation theory of the q-oscillator algebra signal a change in the ground states of the Fermion Model and provide us a tool to further investigate this ground state transition. The significance of the explicit mapping is that it provides a new tool to further probe and tests the detailed physical properties of the fermionic lattice model considered here. In our previous work, some of the correct long-distance physical properties of this model (predicted by the EFT) were somehow hidden in the intricacy of the mappings among the different models and theories used to establish the equivalence of them. The ability to provide more explicit answers to interesting questions arising in the context of this fermionic model gives us hope to use it as a tool to further develop our understanding of the nature of the Mott transition(s). Another goal we had in mind writing this paper was to provide a further link between the three different areas of research common to the type of systems considered here, namely: condensed matter, theoretical and mathematical physics.
. That is, we have provided an explicit link between the Hilbert spaces of a microscopic theory with those of its long distance EFT, something that can not be expected in general systems, although some researchers in the condensed matter community frequently ask for. The changes in the representation theory of the q-oscillator algebra signal a change in the ground states of the Fermion Model and provide us a tool to further investigate this ground state transition. The significance of the explicit mapping is that it provides a new tool to further probe and tests the detailed physical properties of the fermionic lattice model considered here. In our previous work, some of the correct long-distance physical properties of this model (predicted by the EFT) were somehow hidden in the intricacy of the mappings among the different models and theories used to establish the equivalence of them. The ability to provide more explicit answers to interesting questions arising in the context of this fermionic model gives us hope to use it as a tool to further develop our understanding of the nature of the Mott transition(s). Another goal we had in mind writing this paper was to provide a further link between the three different areas of research common to the type of systems considered here, namely: condensed matter, theoretical and mathematical physics.
Acknowledgements
G. R. Zemba is a member of CONICET (Argentina).