QED-Lie Algebra and Their £ -Modules in Superconductivity

Francisco Bulnes

Research Department in Mathematics and Engineering, TESCHA, Chalco, Mexico.

DOI: 10.4236/jamp.2015.34053                

Abstract

It’s created a canonical Lie algebra in electrodynamics with all the “nice” algebraic and geometrical properties of an universal enveloping algebra with the goal of can to obtain generalizations in quantum electrodynamics theory of the TQFT, and the Universe based in lines and twistor bundles to the obtaining of irreducible unitary representations of the Lie groups SO(4) andO(3,1), based in admissible representations of U(1), and SU(n)  . The obtained object haves the advantages to be an algebraic or geometrical space at the same time. This same space of ￡-modules can explain and model different electromagnetic phenomena in superconductor and quantum processes where is necessary an organized transformation of the electromagnetic nature of the space- time and obtain nanotechnologies of the space-time and their elements.

Keywords

Electromagnetic Representation, Electro-Physics Theory, Lie Algebra, £-Modules

1. Introduction: Construction of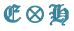, with, and, -Modules

Let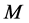, be the space-time whose causal structure [1] (Segal, 1974), is defined by the space

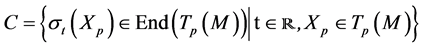
Let the Lorentz group

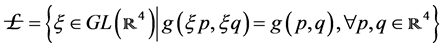
where, and to a local coordinates system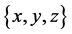,¹

Is the pseudo Riemannian metric of the manifold. If we restrict, to a defined subspace by the light cone

Induced for the orientation of, , results to be an endomorphism of a subspace, of, with the property to be an affine connection in the space-time. Indeed, is the affine connection describes as:

Consider the electromagnetic field or Maxwell field defined as the differential 2-form of the forms space;

Which can be described in the endomorphism space of, by the matrix (where, and, are equal to):

where (respectively) the corresponding form of electric field (respectively magnetic field).

We want to obtain a useful form to define the actions of the group, on the space of electromagnetic fields, which is resulted of generalize to the space, as an anti-symmetric tensor algebra through from induce to the product, in the product, shape that will be useful to the localizing and description of the irreducible unitary representations of the groups, and representations of spinor fields in the space- time furthermore of their characterizing as principal -bundle of.

Likewise, the electromagnetic field is the 2-form given by (6) with the property of the transformation

In, said 2-form match with the -matrix to. Remember that.

In the context of the gauge theories (that is to say, in the context of bundles with connection as the principal -bundles) we first observe that, is an exact form and thus there exists a 1-form (electromagnetic potential) that defines a connection in a -bundle on, and such that²

Consider the -invariant -structure, of the differentiable manifold, with Lorentzian metric (and thus pseudo-Riemannian), on, with, in the system of canonical coordinates

And let the spaces, , two free -modules (modules belonging to a commutative ring with unit) such that

And

where, is Euclidean in, and, is Loretzian in. Such -modules are -modules where, is the orthogonal group of range 4. The two modules in (10) and (11) intrinsically define all electric and magnetic fields, and, in terms of. Thus also their tensor, exterior, and scalar products between elements must be expressed in terms of. To it we consider the tensor product of (10) and (11) free -modules elements, to know³,

where, is light speed and ⁴, is the dual electromagnetic tensor of. Then, what must be?

In the absence of sources, the Maxwell equations are symmetric under a duality transformation, which interchanges electric and magnetic fields.

Proposition 2.1. (F. Bulnes) [2]. Said -modules are invariant under Euclidean movements of the group, and thus are -modules.

Proof. Using the definition of, and and,⁵ defined as the map

With rule of correspondence

where the images of, in, are

Then to a new coordinate system (local reference)

where, are images in, for all, under. Then these images correspond to points in. Thus. Then is a -module. To demonstrate that, is a -module, we consider the coordinate system transformation

Let, be the tensor algebra generated by the elements. Let, be the two-seated ideal generated by the elements, Let, be the Lie algebra whose composition rule is. Its wanted to construct an associative algebra with unity element corresponding to, such that

And such that the -connections in, are the Maxwell tensors, such that

which is completely equivalent to (8). But is enunciated in this moment because it legitimizes the Maxwell tensor from the scalar and vector potentials and we have (12).

We consider the space of electromagnetic power where we will define the domain of electromagnetic space transformation,⁶ that is to say, the cross product of -modules restricted in,

where, is the Poynting vector in. To obtain the 4-tensor of stress energy from this Poynting vector, which represents the particular case of an electromagnetic energy flux vector, is necessary to apply a Lorentz transformation to the -module, to after apply the universal map property of ⁷ having by pro- perties of tensor product of free modules that is:

which is universal in the following sense:

For every Abelian group, and every bilinear map

,

there is a unique group homomorphism

,

such that

for all and where the new elements of the space, are,⁸ where in this case, is a -anti-symmetric second rank tensor of magnetic field.

We want describe energy flux in liquid and elastic media in a completely generalized diffusion of electromagnetic energy from the source view (particles of the space-time), which must be much seemed as a multi-ra- diative tensor insights space or a electromagnetic insights tensor space. This will permits us to express and model the flux of electromagnetic energy and any their characteristics.

The rate of energy transfer (per unit volume) from a region of space equals the rate of work done on a charge distribution plus the energy flux leaving that region.

Of fact these are elements, that are constructed from the power space given in (18) and that conform the electromagnetic energy flux vector space of Poynting, [4] can be extended to, conforming an electromagnetic multi-radiative space with inherence of the metric of the space-time, having the stress-energy- momentum tensor (or the Maxwell stress tensor)

Then a source inside the electromagnetic multi-radiative space is obtained with the divergence, to know:

where. After we use these tensors to characterize the affecting of the space for the superconductor fields having this multi-radiative effect to quantum level, that is to say, obtain a fermionic state in the space-time [5] with anti-gravity created from the analogous tensors to as sources.

2. Lie Algebra Properties

Proposition (F. Bulnes) 3.1. The electrodynamical space, is a closed algebra under the composition law of the -connections.

Proof. [2] [6].

Due to that we are using a torsion-free connection (e.g. the Levi Civita connection), then the partial derivative, used to define, can be replaced with the covariant derivative. The Lie derivative of a tensor is another tensor of the same type, i.e. even though the individual terms in the expression depend on the choice of coordinate system, the expression as a whole result in a tensor in.

Proposition (F. Bulnes) 3.2. The closed algebra, is a Lie algebra.

Proof.

Then the other properties of Lie algebra are trivially satisfied. Thus, haves structure of Lie algebra under the operation.

Proposition (F. Bulnes) 3.3. The closed algebra, is a fibered vector bundle whose fibers are the tangent vectors in each point of the lines of electromagnetic field (geodesics).

Proof. Since as Lie algebra, the space, satisfies that

. Then,

Thus, where by the proposition 2.1, , is the fibred vector bundle of the tangent

vectors, and, which are vectors in, and fibers of the space, whose sections are the, and.

3. Applications

Related with the superconductivity we have the following result:

Theorem (F. Bulnes) 3.1. The electro-anti-gravitational effects produced from superconductivity have that to be governed by the actions of the superconducting Lie-QED-algebra.

Proof. [6].

3.1. The Algebra as QED-Lie Algebra of

We want establish the electromagnetic principle that produce levitation or anti-gravity from the electro-anti- gravitational source that include the proper movements in the space-time that are connected with the actions of the group.

These proper movements are determined through elements of, that acts as “slices” (or orbits of) by the proper object that is levitated, and that provoke iso-rotations (see the lemma [7]) through the

action of their Maxwell fields, given by, in the superconductor. Then can be

calibrate the gravitational elements through electromagnetic elements such that these last can change the gravitational effects changing the spin characteristic of the affected region by these superconductor electromagnetic fields.

The initial ideas to this respect are replace the Abelian group, in the-invariant -structure of the principal -bundle of, by the non-Abelian group, since we want realize an action through electromagnetic fields on a Cosmos representation given by the space (due our lemma [7]) where, is a torus .We want an identification.

We want these identifications because our superconductivity theory establish the principles to risk the electro- anti-gravitational flight of an object as a sidereal object in the space-time, such that a galaxy or a star. In these sidereal objects, there are electromagnetic transformations explained MHD⁹, where the superconducting phenomena go given form the accretion rings, and their rotation (see the Figure 1).

3.2. in the Superconducting Phenomena and Their Electro-Anti-Gravitational Effects

Use through the model that consists of a complex scalar field,¹⁰ minimally coupled to a gauge field given by 1-forms (-gauge field) “coupled to a charged spin 0 scalar field” and that satisfy:

where, has been defined in Section 2.1. We define to, as the covariant derivative of the field, also, is the electric charge and, is the potential for the complex scalar field. This model is invariant under gauge transformations parameterized by, that is to say, are had the following transformations to the fields:

If the potential is such that their minimum occurs at non-zero value of, this model exhibits the Higgs mechanism. This can be seen studying the fluctuations about the lowest energy configuration, one sees that gauge field behaves as a massive field with their mass proportional to the, times the minimum value of. As shown by Nielsen and Olesen [8], this model, in, dimensions, admits time-independent finite energy configurations corresponding to vortices carrying magnetic flux. The magnetic flux carried by these vortices is quantized (in units

of ¹¹) and appears as a topological charge associated with the topological current [9]:

(a) (b)

Figure 1. (a) The cloud energy is created by the superconducting fields in the formatting iso-rotations in a galaxy, this forms, in condensed matter the sidereal objects with autonomous energy; (b) Artificial anti-gravitational wrapping created by superconducting and magnetic rotations. The “spirit of the anti-gravitational effect is in”.

Figure 2. Circulation around a close circuit in a superconductor under a magnetic field. This brings a discrete magnetic flow which means that the magnetic flow has been quantized.

Developing these topological electromagnetic elements using the tensor, we have to two Maxwell tensors:

precisely is our tensor algebra given in proposition 3.1., with their conserved Lie structure.

The essential difference between both versions consists in the coupling to a charged, scalar field, that in this case is a scalar magnetic field corresponding to a magnetic flow associated to the supercurrent.

Considering the supercurrent in presence of magnetic field of vector potential, this takes the form

where, is a function very general of complex type that are changing spatially and that in an any point this function depends of the order parameter (as coherent length, penetration length, etc parameters that are useful to characterize a superconductor [10]) and, is the density of the superconducting electrons.

Considering to an electron field, a representation, where, is a Hilbert space and whose correspondence rule is

And let,¹² the two-sided ideal in the tensor algebra defined in Section 2.1, , generated by the elements of the form, where.

Proposition 2.2.1. There is a natural one-to-one correspondence between the set of all representations of, on, and the set of all representations of, on, If, is a representation of, on, and, , is a representation of, on, then

Proof. [6].

Def. 2.2.1. [11]. A -field is an element of a bi-sided ideal of the Maxwell fields [12] [13]. Explicitly is the formal space

Before of this, we pass to the fundamental lemma to characterize the algebra, as the fundamental algebra of all movements and electromagnetic phenomena (for example, magnetic levitation, electromagnetic matter condensation, Eddy currents, etc.) produced to quantum level by their electromagnetic fields satisfying the variation principle in their field actions.

Lemma (F. Bulnes) [11] 2.2.1. All electromagnetic actions and their effects (microscopic and macroscopic) on the superconductor object, comes from the -fields.

Proof. [9] [11].

3.3. Organized Transformations and Nanotechnology by: Affecting the Space-Time

Theorem (F. Bulnes) 5.1. [6]. The electro-anti-gravitational effects produced from superconductivity have that to be governed by the actions of the superconducting Lie-QED-algebra.

The demonstrations was realized in [6] using some results on iso-rotations which also co-help in the electro- anti-gravitational effect. Likewise, considering two elements of the group, for example, the representation fulfils (by proposition 2.2.1) is

And the field is transformed as

where explicitly the image. From this always is possible construct a second representation defined by:

Which belongs to the charge-conjugated particle. The anti-particle is obtained of accord to the contragradient, representation, which is:

There are not charge-conjugated in gravity, since if the gauge group is Lorentz group, then elements, which means that the second representation, is equivalent to.

But we need affect the immediate space-time at least locally through of these -fields, such that we will have the anti-particles given in (28). Also we need a mapping that involves and include in their image the spin connection that is involved in this anti-gravity process from superconductivity.

We define the field, as a vector field whose application is as given in (26)

,

Under a general diffeomorphism, that is to say, the mapping belonging to the space, where, is the dual to. But we required local transformations at least in the immediate enthrone of object, such that be anti-gravitational and this local enthrone acts with the space-time to create levitation in.

Then the principal equivalence requires that the fields on our manifold locally transform be as in special relativity, that is to say, if, is an element of the Lorentz group,¹³ the fields are transformed like Lorentz-vectors. Of fact this property is extended to all electro-physical modules, and, like -modules (see proposition 2.1, in the introduction).

However, the generalization to a general diffeomorphism is not unique. We could have chosen the field, as a vector field whose applications are

But as, is an element of, that is to say, both representations (29) and (30) agree. For general diffeomorphism that will not be the case, although introducing a new field that have a modified scaling behavior, this can be possible to affect to the space-time by -fields. Then is considered, such that to fields, one finds the behavior

It will be useful to clarify the emerging picture of space-time properties by having a close look at a contravariant vector field, as depicted in the wrapping energy around (see the Figure 1(b)). This field in blue is a cut in the tangent bundle, that is the set of tangent spaces, , which describes our space-time. The field is mapped to their covariant field, which is a cut in the cotangent bundle, by the metric tensor [14]

Then for completeness, let us also define the combined mappings through the relations:

Newly introducing the fields (from here anti-graviting) this is transformed under the local Lorentz trans- formations like a Lorentz-vector in special relativity¹⁴. Then we can have (after of involve the relations of):

where, in the space. Then, , and. Then using the notation, to covariant derivative we have:

which is a new connection. Then the Maxwell-anti-gravity Lagrangian (that is to say, for anti-gravitational pendants, of gauge fields to Maxwell-anti-gravity observable) is introduced via the field tensors:

Staying a Lagrangian of the type (see Section 2.2.1). Here, are the structure constants of the group and, is the charge electron coupling with the Planck scale. Then the corresponding electro-anti-gravitational-Lie-QED-algebra is that with super-currents

4. Conclusion

Different microscopic aspects of electromagnetic nature are analyzed through the construction of an anti-com- mutative algebra of -modules, which can help to define the algebraic and geometrical behavior of the super- currents, sources of energy and power multi-radiative spaces and the Majorana states in fermionic Fock spaces to each one of these applications that in the next one hundred years will be necessary to surviving of the humanity. A classification table of the different versions of the QED-Lie-algebra of accord to the different products of electromagnetic objects obtained can be seeing in Table 1.

Table 1. QED-Lie algebra contexts [15]-[23].

In this table are resumed all the applications mentioned in the sections of this work.

Acknowledgements

I am grateful for the invitation realized by the SCET-2015, organizers to participate with a talk in applied mathematics and physics.

NOTES

²The anti-symmetric nature of this form results obvious:

³This is valid since tensor product of free -modules is a free -module [3]. Here.

⁴The Levi-Civita tensor can be used to construct the dual electromagnetic tensor in which the electric and magnetic components exchange roles (conserving the symmetry, characteristic that can be seen in the matrices of the electromagnetic tensor, and their dual):

where is the rank-4 Levi-Civita tensor density in Minkowski space.

⁵The map is automorphism on.

⁶This defines the hyperbolic paraboloid of the space-time region in a region of electromagnetic power.

⁷Let and, a ring (with right -module, a left -module) be as in the previous section. The tensor product over, , is an Abelian group together with a bilinear map

⁸.

⁹Magneto-Hydrodynamics.

¹⁰In a complex scalar field theory, the scalar field takes values in the complex numbers, rather than the real numbers. The action considered normally takes the form

This has a, or, equivalently, symmetry, whose action on the space of fields rotates, for some real phase angle.

¹¹If, is away from of the borders and rounds to the hollow (see Figure 2) and suppose that is have applied a magnetic field to this superconductor, then

But, (inside the superconductor (or ring in the experimental Figure 2) there not are currents) then

For the Stokes theorem is had that

To it is necessary remember that the superconducting current, haves an unique value in each point, which is equivalent to that the density of superconductor electrons is injective in each point. This bring as consequence that in a close circuit, of length, we have

For the circulation around a close circuit, and considering that

we have that on the close circuit,

that in our case is

¹²Remember that, from a point of view of the superconductors is a topological current associated with the topological charge defined related with the magnetic flux carried by the fluxoids.

¹³.

¹⁴The underlined indices on these quantities do not refer to the coordinates of the manifols, but to the local basis in the tangential. All of these fields still are functions of the space-time coordinates. As diffeomorphism, maps the basis of one space into the other. We can expand it as, or, respectively, such that (have inverses):

¹⁵A electromagnetic case is given by the algebra:.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Segal, I.E. (1976) Mathematical Cosmology and Extragalactic Astronomy. Pure and Applied Mathematics, 68, Academic Press, New York.
[2]	Bulnes, F. (2006) Doctoral Course of Mathematical Electrodynamics. SEPI-IPN, Mexico, 9, 398-447.
[3]	Dummit, D.S. and Foote, R.M. (2004) Abstract Algebra. Wiley, Hoboken.
[4]	Marsden, J.E. and Abraham, R. (1982) Manifolds, Tensor Analysis and Applications. Addison Wesley, Massachusetts.
[5]	Wilczek, F (2009) Majorana Returns. Nature Physics, 5, 614.
[6]	Bulnes, F. (2014) A Lie-QED-Algebra and Their Fermionic Fock Space in the Superconducting Phenomena. Quantum Mechanics, Rijeka.
[7]	Bulnes, F., Hernandez, E. and Maya, J. (2010) Design and Development of an Impeller Synergic System of Electromagnetic Type for Levitation, Suspension and Movement of Symmetrical Bodies, IMECE/ASME, British Columbia, Canada.
[8]	Nielsen, H.B. and Olesen, P. (1973) Vortex-Line Models for Dual Strings. Nuclear Physics B, 61, 45-61.
[9]	Alario, M.A. and Vicent, J.L. (1991) Superconductivity. Eudema Fortuny, Madrid, Spain.
[10]	Ginzburg, V.L. and Landau, L.D. (1950) Zh. Eksp. Teor. Fiz. 20, 1064.
[11]	Bulnes, F., Martínez, I. and Maya, J. (2012) Design and Development of Impeller Synergic Systems of Electromagnetic Type to Levitation/Suspension Flight of Symmetrical Bodies. Journal of Electromagnetic Analysis and Applications, 4, 42-52.
[12]	Bulnes, F. (2013) Orbital Integrals on Reductive Lie Groups and Their Algebras. Intech, Rijeka. http://www.intechopen.com/books/orbital-integrals-on-reductive-lie-groups-and-their-algebras/orbital-integrals-on-reductive-lie-groups-and-their-algebrasB
[13]	Strutinsky, V.M. (1967) Shell Effects in Nuclear Physics and Deformation Energies. Nuclear Physics A, 95, 420-442.
[14]	Hossenfelder, S. (2006) Anti-Gravitation. Elsevier Science.
[15]	Dixmier, J. (1969) Les C*-algèbres et leurs representations. Gauthier-Villars, France.
[16]	Cooper, L. (1956) Bound Electron Pairs in a Degenerate Fermi Gas. Physical Review, 104, 1189-1190.
[17]	Verkelov, I., Goborov, R. and Bulnes, F. (2013) Fermionic Fock Space in Superconducting Phenomena and Their Applications. Journal on Photonics and Spintronics, 2, 19-29.
[18]	Bardeen, J., Cooper, L.N. and Schrieffer, J.R. (1957) Microscopic Theory of Superconductivity. Physical Review, 106, 162-164.
[19]	Bulnes, F. (2013) Mathematical Nanotechnology: Quantum Field Intentionality. Journal of Applied Mathematics and Physics, 1, 25-44.
[20]	Llano, M. (2003) Unificación de la Condensación de Bose-Einstein con la Teoría BSC de Superconductores. Rev. Ciencias Exactas y Naturais, 5, 9-21.
[21]	Bulnes, F. (2013) Quantum Intentionality and Determination of Realities in the Space-Time through Path Integrals and Their Integral Transforms, Advances in Quantum Mechanics, Prof. Paul Bracken (Ed.), InTech. http://www.intechopen.com/books/advances-in-quantum-mechanics/quantum-intentionality-and-determination-of-realities-in-the-space-time-through-path-integrals-and-t
[22]	Landau, L.D. and Lifshitz, E.M. (1960) Electrodynamics of Continuous Media. Volume 8 of Course of Theorical Physics, Pergamon Press, London.
[23]	Bulnes, F. (1998) The Super Canonical Algebra . International Conferences of Electrodynamics in Veracruz, IM/UNAM, Mex-ico.